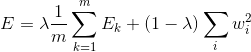BP神经网络原理及实践
一、神经元模型
神经网络： 目前使用最广泛的定义是由适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应。我们在机器学习中谈论神经网络时指的是神经网络学习，或者说，是机器学习与神经网络这两个学科领域的交叉部分。
神经网络中最基本的成分是神经元模型，一直沿用近日的是 “M-P神经元模型”，如下图所示。这个模型中神经元接收到来自 n 个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过激活函数处理以产生神经元的输出。
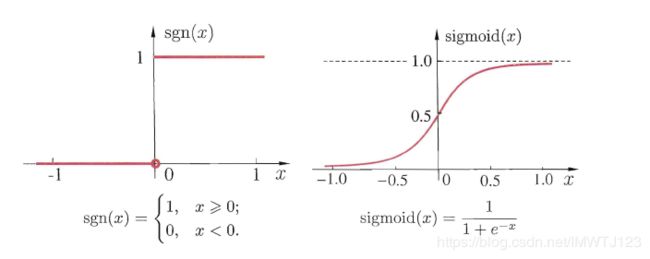
理想中激活函数是阶跃函数，如下图 a 所示，将输入值映射为输出 0 和 1,1 对应神经元的兴奋，0 对应神经元的抑制，但由于阶跃函数具有不连续、不光滑不太好的性质。实际中常用 Sigmoid 函数，如图b所示。它将较大范围内变化的输入值挤压到（0,1）输出值范围内，有时也称“挤压函数”。
(a) (b)
把上述许多个这样的神经元按一定的层次结构连接起来，就得到了神经网络。
二、感知机与多层网络
感知机由两层神经元组成，输出层是“M-P神经元”，亦称“阈值逻辑单元”。感知机能实现逻辑与、或、非运算。感知机的学习规则非常简单，对训练样例（x,y），若当前感知机的输出为 
,则感知机的权重调整为：
其中 
称为学习率，若感知机对训练样例（x,y）预测正确，即 
，则感知机不发生变化，否则将根据错误的程度进行权重调整。由于感知机只有输出层神经元进行激活函数处理，其学习能力非常有限，只能处理线性可分问题。要处理非线性可分问题，需要考虑使用多层功能神经元。例如简单的两层感知机就可以解决异或的问题，在输入和输出有一层神经元，被称为隐含层。隐含层和输出层都具有激活函数的功能神经元。
一般的神经网络如下图所示的单隐层前馈网络，还有双隐层前馈网络等等，只要包含隐含层就为多层网络。每层神经元与下层神经元全连接，神经元之间不存在同层连接，也不存在跨层连接，这样的神经元称为“多层前馈神经网络”。输入层只接受输入不处理函数，隐含层和输出层包含功能函数。
神经网络的学习过程就是训练数据来调整神经元之间的“连接权”以及每个功能神经元的阈值，即神经网络的学习蕴含在连接权和阈值中。
三、BP算法
迄今最成功的神经网络学习算法是误差逆传播算法（BP）,那BP算法究竟是怎样的？ 下面一起来看
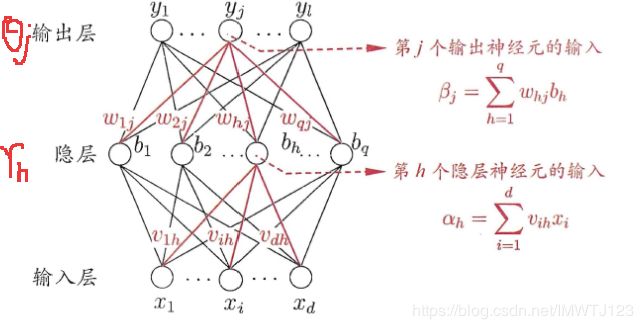
下图是一个拥有 d 个输入神经元，l 个输出神经元，q 个隐含层神经元的多层前馈网络结构。其中输出层第j个神经元的阈值表示为 
，隐含层第 h 个神经元的阈值用 
表示，输入层第 i 个神经元与隐含层第 h 个神经元之间的连接权用 
表示，隐含层第 h 个神经元与输出层第 j 个神经元之间的连接权为 
表示。假设隐含层和输出层神经元都使用 sigmoid 函数。
学习率控制着算法每一轮迭代中的更新步长，若太大则容易震荡，太小收敛速度又会过慢。一般地常把 η 设置为 0.1，有时更新权重时会将输出层与隐含层设置为不同的学习率。
下面给出 BP 算法的工作流程，此流程是针对单个 
推导的，每次更新只针对单个样例，即标准 BP 算法。
但 BP 算法的目的是要最小化训练集 D 上的累积误差：
所以基于累积误差最小化的更新准则，就得到累积误差逆传播算法，即累计 BP 算法，他在读取整个训练集 D 一遍后才对参数进行更新，其参数更新的频率低得多。在很多任务中，累积误差下降到一定程度，进一步下将会非常缓慢，这是标准 BP 往往会更快获得较好的解，尤其在训练集 D 非常大时。
由于BP神经网络的强大，往往会过拟合，其训练误差持续降低，但测试误差会持续上升。有两种方法缓减过拟合：
- 早停：若训练集误差降低但验证集误差升高，则停止训练，同时返回具有验证集误差的连接权和阈值。
- 正则化：其基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分，例如连接权和阈值的平方和。其中 λ∈（0,1）用于对累积经验误差与网络复杂度这两项进行折中，常通过交叉验证法来估计。
在后面将进行BP算法的实践
四、全局最小和局部最小
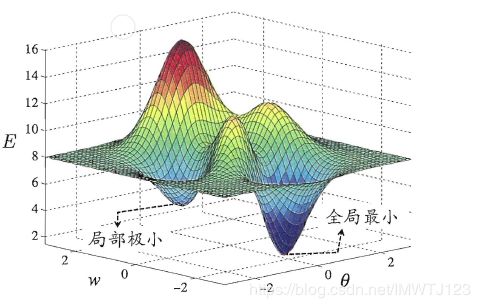
神经网络的训练过程可看作一个参数寻优的过程，即在参数空间中，寻找一组最优参数使得E最小。BP算法试图通过最速下降来寻找使得累积经验误差最小的权值与阈值，在谈到最优时，一般会提到局部极小和全局最小。
局部最小解是参数空间中的某个点，其领域点的误差函数值均小于该点的函数值；
全局最小解之参数空间中所有点的误差函数值均小于该点的误差函数值。两者对应的E就是误差函数的局部极小值和全局极小值。局部极小可以有多个，而全局最小只有一个。全局最小一定是局部极小，但局部最小却不一定是全局最小。显然在很多机器学习算法中，都试图找到目标函数的全局最小。梯度下降法的主要思想就是沿着负梯度方向去搜索最优解，负梯度方向是函数值下降最快的方向，若迭代到某处的梯度为0，则表示达到一个局部最小，参数更新停止。然而，如果误差函数具有多个局部极小，则不能保证找到的就为全局最小，对于这种情况我们称参数寻优陷入局部极小。人们常采用以下策略尽可能地去接近全局最小，即跳出局部极小：
- 以多组不同参数值初始化多个神经网络，按标准方法训练，迭代停止后，取其中误差最小的解作为最终参数。
- 使用“模拟退火”技术，在每一步都以一定的概率接受比当前解更差的结果，从而有助于跳出局部极小。
- 使用随机梯度下降，即在计算梯度时加入了随机因素，使得在局部最小时，计算的梯度仍可能不为零，这样有机会跳出局部极小继续搜索。
此外，遗传算法也常用来训练神经网络以更好地逼近全局最小。上述跳出局部极小的技术大多是启发式，理论上尚缺乏保障。
五、深度学习
参数越多的模型复杂度越高，复杂模型的训练效率低，易陷入过拟合，随着大数据、云计算的时代到来，以深度学习为代表的复杂模型开始受到人们的关注。
对神经网络增加模型复杂度的方法有两种：
- 增加隐含层的数目，隐含层多了相应的神经元连接权、阈值等参数就会更多；
- 单纯增加隐含层神经元的数目。
但从增加模型复杂度的角度来看，增加隐含层的数目比增加隐含层神经元的数目更有效，因为增加隐含层不仅增加拥有激活函数的神经元数目，还增加了激活函数嵌套的层数。然而，多层神经网络难以直接用经典算法（例如标准BP算法）进行训练，因为误差在多隐含层内逆传播时，往往会发散而不能收敛到稳定状态。这里的多隐含层是指三个以上的隐含层，深度学习模型通常有八九层甚至更多层。
所以要有效的训练多隐含层网络通常有两种有效手段：
- 无监督逐层训练：每次训练一层隐节点，把上一层隐节点的输出当作输入来训练，本层隐结点训练好后，输出再作为下一层的输入来训练，这称为预训练。预训练完成后，再对整个网络进行微调训练。例如深度信念网络（deep belief network，简称DBN）。“预训练+微调“可以视为把大量的参数进行分组，先找出每组较好的设置，再基于这些局部最优的结果来进行全局寻优。
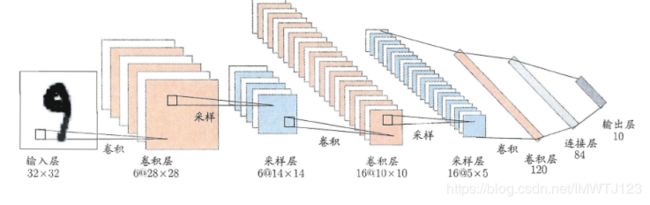
- 权共享：让一组神经元使用完全相同的连接权，例子是卷积神经网络（Convolutional Neural Network，简称CNN）。这样做可以大大减少需要训练的参数数目。以CNN进行手写数字识别任务为例，如下图所示，CNN复合多个卷积层和采样层对输入信号进行加工，然后在连接层实现与输出目标之间的映射。
我们从另一个角度理解深度学习：通过多层处理，逐渐将初始的”低层”特征表示转化为“高层”特征表示后，用“简单模型”即可完成复杂的分类等学习任务，由此可将深度学习理解为进行特征学习或表示学习。
六、BP神经网络的训练
对神经网络的学习大致包括以下步骤：
- 初始化参数，包括权重、偏置、网络层结构、激活函数等。
- 循环计算
- 正向传播，计算误差
- 反向传播，调整参数
- 返回最终的神经网络模型
# -*- coding: utf-8 -*-
"""
Created on Wed Mar 20 09:58:16 2019
@author: 2018061801
"""
import numpy as np
from math import sqrt
def load_data(file_name):
'''导入数据
input: file_name(string):文件的存储位置
output: feature_data(mat):特征
label_data(mat):标签
n_class(int):类别的个数
'''
# 1、获取特征
f = open(file_name) # 打开文件
feature_data = []
label_tmp = []
for line in f.readlines():
feature_tmp = []
lines = line.strip().split("\t")
for i in range(len(lines) - 1):
feature_tmp.append(float(lines[i]))
label_tmp.append(int(lines[-1]))
feature_data.append(feature_tmp)
f.close() # 关闭文件
# 2、获取标签
m = len(label_tmp)
n_class = len(set(label_tmp)) # 得到类别的个数
label_data = np.mat(np.zeros((m, n_class)))
for i in range(m):
label_data[i, label_tmp[i]] = 1
return np.mat(feature_data), label_data, n_class
def sig(x):
'''Sigmoid函数
input: x(mat/float):自变量，可以是矩阵或者是任意实数
output: Sigmoid值(mat/float):Sigmoid函数的值
'''
return 1.0 / (1 + np.exp(-x))
def partial_sig(x):
'''Sigmoid导函数的值
input: x(mat/float):自变量，可以是矩阵或者是任意实数
output: out(mat/float):Sigmoid导函数的值
'''
m, n = np.shape(x)
out = np.mat(np.zeros((m, n)))
for i in range(m):
for j in range(n):
out[i, j] = sig(x[i, j]) * (1 - sig(x[i, j]))
return out
def hidden_in(feature, w0, b0):
'''计算隐含层的输入
input: feature(mat):特征
w0(mat):输入层到隐含层之间的权重
b0(mat):输入层到隐含层之间的偏置
output: hidden_in(mat):隐含层的输入
'''
m = np.shape(feature)[0]
hidden_in = feature * w0
for i in range(m):
hidden_in[i, ] += b0
return hidden_in
def hidden_out(hidden_in):
'''隐含层的输出
input: hidden_in(mat):隐含层的输入
output: hidden_output(mat):隐含层的输出
'''
hidden_output = sig(hidden_in)
return hidden_output;
def predict_in(hidden_out, w1, b1):
'''计算输出层的输入
input: hidden_out(mat):隐含层的输出
w1(mat):隐含层到输出层之间的权重
b1(mat):隐含层到输出层之间的偏置
output: predict_in(mat):输出层的输入
'''
m = np.shape(hidden_out)[0]
predict_in = hidden_out * w1
for i in range(m):
predict_in[i, ] += b1
return predict_in
def predict_out(predict_in):
'''输出层的输出
input: predict_in(mat):输出层的输入
output: result(mat):输出层的输出
'''
result = sig(predict_in)
return result
def bp_train(feature, label, n_hidden, maxCycle, alpha, n_output):
'''计算隐含层的输入
input: feature(mat):特征
label(mat):标签
n_hidden(int):隐含层的节点个数
maxCycle(int):最大的迭代次数
alpha(float):学习率
n_output(int):输出层的节点个数
output: w0(mat):输入层到隐含层之间的权重
b0(mat):输入层到隐含层之间的偏置
w1(mat):隐含层到输出层之间的权重
b1(mat):隐含层到输出层之间的偏置
'''
m, n = np.shape(feature)
# 1、初始化
w0 = np.mat(np.random.rand(n, n_hidden))
w0 = w0 * (8.0 * sqrt(6) / sqrt(n + n_hidden)) - \
np.mat(np.ones((n, n_hidden))) * \
(4.0 * sqrt(6) / sqrt(n + n_hidden))
b0 = np.mat(np.random.rand(1, n_hidden))
b0 = b0 * (8.0 * sqrt(6) / sqrt(n + n_hidden)) - \
np.mat(np.ones((1, n_hidden))) * \
(4.0 * sqrt(6) / sqrt(n + n_hidden))
w1 = np.mat(np.random.rand(n_hidden, n_output))
w1 = w1 * (8.0 * sqrt(6) / sqrt(n_hidden + n_output)) - \
np.mat(np.ones((n_hidden, n_output))) * \
(4.0 * sqrt(6) / sqrt(n_hidden + n_output))
b1 = np.mat(np.random.rand(1, n_output))
b1 = b1 * (8.0 * sqrt(6) / sqrt(n_hidden + n_output)) - \
np.mat(np.ones((1, n_output))) * \
(4.0 * sqrt(6) / sqrt(n_hidden + n_output))
# 2、训练
i = 0
while i <= maxCycle:
# 2.1、信号正向传播
# 2.1.1、计算隐含层的输入
hidden_input = hidden_in(feature, w0, b0) # mXn_hidden
# 2.1.2、计算隐含层的输出
hidden_output = hidden_out(hidden_input)
# 2.1.3、计算输出层的输入
output_in = predict_in(hidden_output, w1, b1) # mXn_output
# 2.1.4、计算输出层的输出
output_out = predict_out(output_in)
# 2.2、误差的反向传播
# 2.2.1、隐含层到输出层之间的残差
delta_output = -np.multiply((label - output_out), partial_sig(output_in))
# 2.2.2、输入层到隐含层之间的残差
delta_hidden = np.multiply((delta_output * w1.T), partial_sig(hidden_input))
# 2.3、 修正权重和偏置
w1 = w1 - alpha * (hidden_output.T * delta_output)
b1 = b1 - alpha * np.sum(delta_output, axis=0) * (1.0 / m)
w0 = w0 - alpha * (feature.T * delta_hidden)
b0 = b0 - alpha * np.sum(delta_hidden, axis=0) * (1.0 / m)
if i % 100 == 0:
print ("\t-------- iter: ", i, \
" ,cost: ", (1.0/2) * get_cost(get_predict(feature, w0, w1, b0, b1) - label))
i += 1
return w0, w1, b0, b1
def get_cost(cost):
'''计算当前损失函数的值
input: cost(mat):预测值与标签之间的差
output: cost_sum / m (double):损失函数的值
'''
m,n = np.shape(cost)
cost_sum = 0.0
for i in range(m):
for j in range(n):
cost_sum += cost[i,j] * cost[i,j]
return cost_sum / m
def get_predict(feature, w0, w1, b0, b1):
'''计算最终的预测
input: feature(mat):特征
w0(mat):输入层到隐含层之间的权重
b0(mat):输入层到隐含层之间的偏置
w1(mat):隐含层到输出层之间的权重
b1(mat):隐含层到输出层之间的偏置
output: 预测值
'''
return predict_out(predict_in(hidden_out(hidden_in(feature, w0, b0)), w1, b1))
def save_model(w0, w1, b0, b1):
'''保存最终的模型
input: w0(mat):输入层到隐含层之间的权重
b0(mat):输入层到隐含层之间的偏置
w1(mat):隐含层到输出层之间的权重
b1(mat):隐含层到输出层之间的偏置
output:
'''
def write_file(file_name, source):
f = open(file_name, "w")
m, n = np.shape(source)
for i in range(m):
tmp = []
for j in range(n):
tmp.append(str(source[i, j]))
f.write("\t".join(tmp) + "\n")
f.close()
write_file("weight_w0", w0)
write_file("weight_w1", w1)
write_file("weight_b0", b0)
write_file("weight_b1", b1)
def err_rate(label, pre):
'''计算训练样本上的错误率
input: label(mat):训练样本的标签
pre(mat):训练样本的预测值
output: rate[0,0](float):错误率
'''
m = np.shape(label)[0]
err = 0.0
for i in range(m):
if label[i, 0] != pre[i, 0]:
err += 1
rate = err / m
return rate
if __name__ == "__main__":
# 1、导入数据
print ("--------- 1.load data ------------")
feature, label, n_class = load_data("D:/anaconda4.3/spyder_work/data.txt")
# 2、训练网络模型
print ("--------- 2.training ------------")
w0, w1, b0, b1 = bp_train(feature, label, 20, 1000, 0.1, n_class)
# 3、保存最终的模型
print ("--------- 3.save model ------------")
save_model(w0, w1, b0, b1)
# 4、得到最终的预测结果
print ("--------- 4.get prediction ------------")
result = get_predict(feature, w0, w1, b0, b1)
print ("训练准确性为：", (1 - err_rate(np.argmax(label, axis=1), np.argmax(result, axis=1))))
结果：
--------- 1.load data ------------
--------- 2.training ------------
-------- iter: 0 ,cost: 0.32056240323748886
-------- iter: 100 ,cost: 0.02374088596119964
-------- iter: 200 ,cost: 0.016247175730753252
-------- iter: 300 ,cost: 0.014216291822320076
-------- iter: 400 ,cost: 0.012527987143185957
-------- iter: 500 ,cost: 0.011411808088174234
-------- iter: 600 ,cost: 0.010691849370465361
-------- iter: 700 ,cost: 0.01007772478527919
-------- iter: 800 ,cost: 0.009571297239877182
-------- iter: 900 ,cost: 0.009190086607128702
-------- iter: 1000 ,cost: 0.008898688196057304
--------- 3.save model ------------
--------- 4.get prediction ------------
训练准确性为： 0.99注： 我使用 Python3.5 ， 测试部分可以自己去试试
训练数据
参考文献：赵志勇《python 机器学习算法》（程序）
周志华《机器学习》（原理）