链表和树
1.什么是单链表
单链表是一种链式存取的数据结构,用一组地址任意的存储单元存放线性表中的数据元素。链表中的数据是以结点来表示的,每个结点的构成:元素(数据元素的映象) + 指针(指示后继元素存储位置),元素就是存储数据的存储单元,指针就是连接每个结点的地址数据。
链表中的数据是以结点来表示的,每个结点的构成:元素(数据元素的映象) + 指针(指示后继元素存储位置),元素就是存储数据的存储单元,指针就是连接每个结点的地址数据。
以"结点的序列"表示线性表称作线性链表(单链表)
单链表是链式存取的结构,为找第 i 个数据元素,必须先找到第 i-1 个数据元素。
因此,查找第 i 个数据元素的基本操作为:移动指针,比较 j 和 i
1.1、链接存储方法
链接方式存储的线性表简称为链表(Linked List)。
链表的具体存储表示为:
①用一组任意的存储单元来存放线性表的结点(这组存储单元既可以是连续的,也可以是不连续的)
②链表中结点的逻辑次序和物理次序不一定相同。为了能正确表示结点间的逻辑关系,在存储每个结点值的同时,还必须存储指示其后继结点的地址(或位置)信息(称为指针(pointer)或链(link))
注意:
链式存储是最常用的存储方式之一,它不仅可用来表示线性表,而且可用来表示各种非线性的数据结构。
1.2、链表的结点结构
┌───┬───┐
│data │next │
└───┴───┘
data域--存放结点值的数据域
next域--存放结点的直接后继的地址(位置)的指针域(链域)
注意:
①链表通过每个结点的链域将线性表的n个结点按其逻辑顺序链接在一起的。
②每个结点只有一个链域的链表称为单链表(Single Linked List)。
/*
* 节点类
*/
public class MyNode {
// 单向列表节点的指针
MyNode next;
// 定义数据
public E item;//数据
public MyNode(E item) {
this.item = item;
}
}
/*
* 链表类
*/
public class MyLinkedList {
// 定义链表的大小
public int size;
public MyNode first;// 第一个节点
public MyNode last;// 最后一个节点
// 添加元素
public void add(E item) {
MyNode myNode = new MyNode(item);
if (first == null) {
first = myNode;
}
if (last != null) {
last.next = myNode;
}
last = myNode;
size++;
}
//删除元素
public E remove(int index) {
if (index < 0 || index > size) {
try {
throw new Exception("角标越界");
} catch (Exception e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
E result = null;
// 遍历到你要删除元素的前一个
MyNode pre = first;
for (int i = 0; i < index - 1; i++) {
pre = pre.next;
}
// 删除头部
if (index == 0) {
result = first.item;
first = first.next;
// 第一个空
pre = null;
} else if (index == size - 1) {// 删除尾部
// 找到最后一个元素。给结果值赋值
result = last.item;
pre.next = null;
last = pre;
} else {// 删除中间的
// 首选要找到删除节点
MyNode self = pre.next;
result = self.item;
pre.next = self.next;
self = null;
}
size--;
return result;
}
//插入元素
public void insert(int index,E item){
size++;
if (index < 0 || index > size) {
try {
throw new Exception("角标越界");
} catch (Exception e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
MyNode pre = first;
MyNode myNode = new MyNode(item);
// 遍历到你要插入元素的前一个
for (int i = 0; i < index - 1; i++) {
pre = pre.next;
}
// 插入头部
if (index == 0) {
first=myNode;
first.next=pre;
} else if (index == size - 1) {// 插入尾部
last.next=myNode;
last=myNode;
} else {// 插入中间
MyNode node=pre.next;
pre.next=myNode;
myNode.next=node;
}
}
//修改元素
public void update(int index,E item){
if (index < 0 || index > size) {
try {
throw new Exception("角标越界");
} catch (Exception e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
//遍历到要修改的元素
MyNode pre = first;
for (int i = 0; i < index; i++) {
pre = pre.next;
}
pre.item=item;
}
// 获取元素
public E get(int index) {
if (index < 0 || index > size) {
try {
throw new Exception("角标越界");
} catch (Exception e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
MyNode result = first;
for (int i = 0; i < index; i++) {
result = result.next;
}
return result.item;
}
public static void main(String[] args) {
MyLinkedList link = new MyLinkedList();
link.add("张三");
link.add("李四");
link.add("王五");
link.update(0, "积极");
link.insert(0, "萧山1");
link.insert(1, "萧山2");
link.insert(5, "萧山6");
link.remove(5);
for (int i = 0; i < link.size; i++) {
System.out.println(link.get(i));
}
}
}
2.什么是双链表
双向链表也叫双链表,是链表的一种,它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。一般我们都构造双向循环链表。
双(向)链表中有两条方向不同的链,即每个结点中除next域存放后继结点地址外,还增加一个指向其直接前趋的指针域prior。
注意:
①双链表由头指针head惟一确定的。
②带头结点的双链表的某些运算变得方便。
③将头结点和尾结点链接起来,为双(向)循环链表。
/*
* 节点类
*/
public class MyNode {
//后驱节点
MyNode next;
//前驱节点
MyNode pre;
// 定义数据
E item;
public MyNode(E item) {
this.item = item;
}
}
/*
* 双向链表
*/
public class MyLinkedList {
// 定linkedlist的大小
public int size;
// 定义第一个节点和最后一个节点
public MyNode first;
public MyNode last;
// 添加元素
public void add(E item) {
// 构建节点存入数据
MyNode node = new MyNode(item);
// 两种第一次添加,还有是不是第一次添加的情况
if (first == null) {
first = node;
first.pre = null;
first.next = null;
}
if (last != null) {
last.next = node;
node.pre = last;
}
last = node;
size++;
}
public E remove(int index) {
if (index < 0 || index > size) {
try {
throw new Exception("角标越界");
} catch (Exception e) {
e.printStackTrace();
}
}
E result = null;
// 遍历到你要删除元素的前一个
MyNode before = first;
for (int i = 0; i < index - 1; i++) {
before = before.next;
}
// 删除头部
if (index == 0) {
result = first.item;
first = first.next;
first.pre = null;
} else if (index == size - 1) {// 删除尾部
// 找到最后一个元素。给结果值赋值
result = last.item;
before.next = null;
last = before;
} else {// 删除中间的
// 首选要找到删除节点
MyNode self = before.next;
result = self.item;
before.next = self.next;
self.next.pre = before;
self = null;
}
size--;
return result;
}
//插入
public void insert(int index, E data) {
if (index < 0 || index > size) {
try {
throw new Exception("角标越界");
} catch (Exception e) {
e.printStackTrace();
}
}
// 遍历到要要插入前一个节点
MyNode before = first;
for (int i = 0; i < index - 1; i++) {
before = before.next;
}
// 构建一个你要插入的节点
MyNode myNode = new MyNode(data);
if (index == 0) {
myNode.next = before;
before.pre = myNode;
first = myNode;
size++;
} else {
myNode.next = before.next;
before.pre = myNode;
before.next = myNode;
myNode.pre = before;
size++;
}
}
//修改元素
public void update(int index,E item){
if (index < 0 || index > size) {
try {
throw new Exception("角标越界");
} catch (Exception e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
//遍历到要修改的元素
MyNode before = first;
for (int i = 0; i < index; i++) {
before = before.next;
}
before.item=item;
}
// 获取元素
public E get(int index) {
if (index < 0 || index > size) {
try {
throw new Exception("角标越界");
} catch (Exception e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
MyNode result = first;
for (int i = 0; i < index; i++) {
result = result.next;
}
return result.item;
}
public static void main(String[] args) {
MyLinkedList link = new MyLinkedList();
link.add("张三");
link.add("李四");
link.add("王五");
link.insert(1, "ll");
link.update(2, "33");
link.remove(3);
for (int i = 0; i < link.size; i++) {
System.out.println(link.get(i));
}
}
}
3.什么是树
树:是由n(n>=1)个有限节点组成一个具有层次关系的集合
树术语
节点度:一个节点含有子树的个数称为该节点的度
树的度:一棵树中,最大的节点的度为树的度
叶子节点:度为零的节点
父亲节点:若一个节点含有子节点,则当前节点为改子节点的父亲节点
子节点:一个节点含有子树,则子树的根节点为改节点的子节点
兄弟节点:具有相同父亲节点的子节点互为兄弟节点
节点层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推
树的深度(高度):树中节点最大的层次
其他:堂兄弟节点、子孙、森林
树的分类
无序树:树中的节点次序是没有规律的
有序树:指树中同层结点从左到右有次序排列,这样的树称为有序树。
1)二叉树:每个节点最多含有两个子树的树称为二叉树
2)非二叉树:所有不是二叉树的树都属于非二叉树
4.什么是二叉树
二叉树是一种特殊的树形结构,每个节点至多只有两颗子树,并且子树有左右之分,其次序不能随意颠倒,是有序树的一种。
注意:二叉树是由一个根结点、两棵互不相交的左子树和右子树组成。
二叉树分类
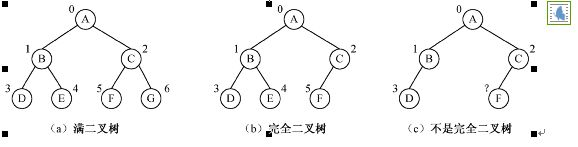
满二叉树:对于上述的完全二叉树,如果去掉其第d层的所有节点,那么剩下的部分就构成一个满二叉树
完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树;
完全二叉树性质
若根结点的层次为1,则二叉树第i层最多有2的(i-1)次方个结点。
在高度为k的二叉树中,则最多有2k-1个结点(k≥0)
设一棵二叉树节点个数为n,则父节点个数为n/2。
一棵具有n个结点的完全二叉树,对序号为i(0≤i
若i=0,则i为根结点,无父母结点;若i >0,则i的左右子结点序号为:
若2i+1
若2i+2
树的遍历
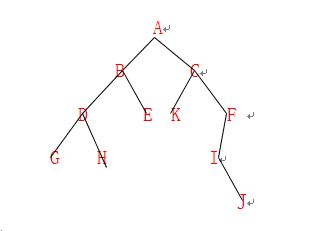
先序遍历树
先访问根节点,然后访问左子树,最后访问右子树ABDGHECKFIJ
中序遍历树
先访问左子树,然后访问根节点,最后访问右子树GDHBEAKCIJF
后续遍历树
先访问左子树,然后访问右子树,最后访问根节点GHDEBKJIFCA
/*
* 树节点类
*/
public class TreeNode {
TreeNode left;//左节点
TreeNode right;//右节点
int value;
public TreeNode(int value) {
this.value=value;
}
public TreeNode getLeft() {
return left;
}
public void setLeft(TreeNode left) {
this.left = left;
}
public TreeNode getRight() {
return right;
}
public void setRight(TreeNode right) {
this.right = right;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
}
/*
* 二叉树类
*/
public class CreatTreeModel {
int[] arr;
ArrayList list = new ArrayList();
public CreatTreeModel(int[] arr) {
super();
this.arr = arr;
}
// 构造树
public TreeNode creatTree() {
// 将数组里的元素用节点封装
for (int i = 0; i < arr.length; i++) {
TreeNode treeNode = new TreeNode(arr[i]);
list.add(treeNode);
}
// 构造二叉树
// 遍历父亲节点
for (int i = 0; i < list.size() / 2 - 1; i++) {
list.get(i).setLeft(list.get(2 * i + 1));
list.get(i).setRight(list.get(2 * i + 2));
}
// 将最后一个节点单独处理
int lastIndex = list.size() / 2 - 1;
TreeNode treeNode = list.get(lastIndex);
treeNode.setLeft(list.get(2 * lastIndex + 1));
if (list.size() % 2 == 1) {
// 满二叉树
treeNode.setRight(list.get(2 * lastIndex + 2));
}
// 返回根节点
return list.get(0);
}
// 前序遍历
public void beforSearch(TreeNode root) {
// 根
System.out.println(root.getValue());
// 左
if (root.getLeft() != null) {
beforSearch(root.getLeft());
}
// 右
if (root.getRight() != null) {
beforSearch(root.getRight());
}
}
// 中序遍历
public void midSearch(TreeNode root) {
// 左
if (root.getLeft() != null) {
midSearch(root.getLeft());
}
// 根
System.out.println(root.getValue());
// 右
if (root.getRight() != null) {
midSearch(root.getRight());
}
}
// 后序遍历
public void lastSearch(TreeNode root) {
// 左
if (root.getLeft() != null) {
lastSearch(root.getLeft());
}
// 右
if (root.getRight() != null) {
lastSearch(root.getRight());
}
// 根
System.out.println(root.getValue());
}
public static void main(String[] args) {
int[] arr = { 11, 22, 55, 1, 2, 5, 7 };
CreatTreeModel ct = new CreatTreeModel(arr);
TreeNode creatTree = ct.creatTree();
ct.beforSearch(creatTree);
//ct.midSearch(creatTree);
//ct.lastSearch(creatTree);
}
}