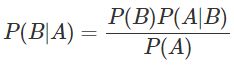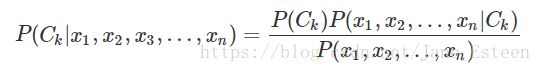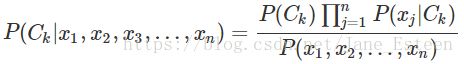朴素贝叶斯学习笔记

1.1 贝叶斯公式

P(B|A): 事件A发生条件下事件B发生的概率，即后验概率；

P(B): 事件B发生的概率，即先验概率；

P(A|B): 事件B发生条件下事件A发生的概率，即条件概率。

1.2 特征条件独立假设

要求后验概率，麻烦的点在于条件概率的参数太多，有着指数级数量的参数，假设：

（上头的参数个数是《统计学习方法》第47页给出的 ，我不太理解，举个例子，如果有两个特征X1，X2，各有3种取值，标签为Y，有两个取值，按李航老师的说法，要求的参数就是2*3*3 = 18种。可是

P(X1,X2 | Y) = P(X1 | X2,Y) * P(X2 | Y), 分解后，第一部分的参数应该是3 * 3 * 2，第二部分的参数是3 * 2，加起来要求的参数就是18 + 6 = 24种。你可能会想不要分解啊，P(X1,X2 | Y) 里头就有3 * 3 * 2 = 18种组合，那就是18个参数，可是不分解你咋求？问题未完，等我整理完条件概率独立再接着说。。。）

所以朴素贝叶斯要对条件概率分布作条件独立性的假设，这样一来后验概率求解公式就是：

（续上头的例子，这里说参数规模降到2 * (3 + 3) = 12种，这很合理啊，因为条件概率独立的时候，P(X1,X2 | Y) = P(X1 | Y) * P(X2 | Y)，这里要求的参数的确是3 * 2 + 3 * 2 = 12种。所以说要分解之后你才会知道究竟要算多少个参数。假设要写个程序，给定一个数据集，随便给特征，就要算出归为哪一类，那么通常做法就是先定义一个函数，把数据集所有要求的参数求出来，在定义一个计算的函数，用来算后验概率，然后给啥特征，查啥特征相应的条件概率，先验概率，再用定义的计算函数算出后验概率。条件概率分布独立之后参数个数没有任何疑惑，可是没有独立的个数真只有3 * 3 * 2种？有没有人理解了我的困惑，并且不吝爱心回答下我~）

补充一句，我们的目标就是后验概率最大化，用以确定给定一系列特征究竟该归为哪一类。

1.3 极大似然估计

我真诚的希望我写的博客能兼具实用与美观，可是我又在欺骗我自己了。

以下公式暂时似懂非懂就可以了，因为自己动手算过才会理解公式之美。

1.4 贝叶斯估计

贝叶斯估计啊就是在极大似然估计的基础上加一个laplace平滑，这样做的原因是，如果你输入了一个特征值，可是在训练集里，给定标签是找不到对应的这个特征值的，那么这个特征值的条件概率肯定为0，后果就是条件概率的连乘就会变成0，紧接着后验概率也变成0，其他特征的条件概率大概会觉得很委屈。

所以呢贝叶斯估计就考虑到了这点，条件概率公式分子分母都加一个平滑项，这样分子为0不会造成条件概率为0，分子和分母一样的时候，分子加1就会概率大于1，分母也加一个平滑项就能解决这个问题了。看公式(4.10）

1.5 动手实践（R）

# 多项式模型
a = data.frame(x1 = c(rep(1:3,each = 5)),x2 = c("S",rep("M",2),rep("S",3),rep("M",2),rep("L",3),rep("M",2),rep("L",2)),
               y = c(-1,-1,1,1,-1,-1,-1,rep(1,7),-1))  # 数据
a$y <- factor(a$y) # 把类别变量变成因子型变量
laplace <- 1 # 定义平滑值
vars = names(a) # 所有变量名
vars = vars[-length(vars)] # 剔除因变量后的变量
prior <- table(a$y,dnn = c("y")) # 求先验概率的准备工作
prior_prob <- (prior + laplace)/(sum(prior) + laplace * nlevels(a$y)) # 先验概率
tables <- sapply(vars,function(x){
  tab = table(a$y,a[[x]],dnn = c("",x))
  t((tab + laplace)/(rowSums(tab) + laplace * ncol(tab)))
},simplify = FALSE) # 条件概率
# 给定x = (2,S)计算： 
p1 <- prior_prob[[2]] * tables$x1["2","1"] * tables$x2["S","1"] # P(y = 1) * P(x1 = 1|y = 1) * P(x2 = "S"|y = 1)
p2 <- prior_prob[[1]] * tables$x1["2","-1"] * tables$x2["S","-1"] # P(y = -1) * P(x1 = 1|y = -1) * P(x2 = "S"|y = -1)

上面的代码是针对特征是离散变量来的，如果特征是连续的呢，这个时候就可以假装特征变量都是服从正太分布，算出均值标准差，不就可以很轻易的随意赋值，再算出相应的概率密度值了吗，概率密度值虽然不是概率，可是还是能说明这个特征值出现的相对概率。

# 高斯模型
b = data.frame("height" = c(6,5.92,5.58,5.92,5,5.5,5.42,5.75),
               "weight" = c(180,190,170,165,100,150,130,150),
               "foot" = c(12,11,12,10,6,8,7,9),
               "gender" = c(rep("male",4),rep("female",4)))

b$gender <- factor(b$gender)
vars = names(b) # 所有变量名
vars = vars[-length(vars)] # 剔除因变量后的变量
prior <- table(b$gender,dnn = c("gender")) # 求先验概率的准备工作
prior_prob <- (prior + laplace)/(sum(prior) + laplace * nlevels(b$gender)) # 先验概率
tables <- sapply(vars,function(x){
  tab <- rbind(tapply(b[[x]],b$gender,mean),
               tapply(b[[x]],b$gender,stats::sd))
  rownames(tab) <- c("mean", "sd")
  as.table(tab)
},simplify = FALSE) # 条件概率
# 给定x = (6,130,8)计算： 
p1 <- prior_prob[[2]] * dnorm(6,tables$height["mean","male"], tables$height["sd","male"])*
                        dnorm(130,tables$weight["mean","male"], tables$weight["sd","male"])*
                        dnorm(8,tables$foot["mean","male"], tables$foot["sd","male"])   
p2 <- prior_prob[[1]] * dnorm(6,tables$height["mean","female"], tables$height["sd","female"])*
                        dnorm(130,tables$weight["mean","female"], tables$weight["sd","female"])*
                        dnorm(8,tables$foot["mean","female"], tables$foot["sd","female"])
p2/p1 > 1000

还有一种模型叫做伯努利模型，这种和多项式模型很像，只不过特征变量必须非零即1，所以要对特征二值化，其他都一样啦。

最后，理解这个算法怎么实现之后，真要用的时候就可以调包啦。

library(e1071)
a$x1 <- as.character(a$x1); a$x2 <- as.character(a$x2) ; a$y <- as.factor(a$y) # 如果特征不是数值变量，这个包就会算概率
a2 = naiveBayes(y ~., data = a,laplace = 1)
(a3 = predict(a2,data.frame(x1 = 2,x2= "S"),type = "class"))

b$gender <- as.factor(b$gender) # 如果特征是数值变量，就默认数值变量服从高斯分布，用概率密度值来代替概率
b2 = naiveBayes(gender ~., data = b)
(b3 = predict(b2,data.frame(height = 6,weight= 130,foot = 8),type = "class"))

还没完，我还想补充下这个算法的优缺点：

缺点：假设过强，分类性能不一定高。

优点：算法高效，易于实现。