机器学习基石（林轩田）第六章 笔记与感悟总结

6.1 Theory of Generalization - Restriction of Break Point

机器学习领域机器是如何做到举一反三的本领的？   dichotomies 是二分类 ，即label只有（o，x）这种。

例如positive rays，意思是一侧全是正，另一侧全是负，而出现ox 这种情景时，则两个点的mh（2）=3，实现了小于2^2的目的。突破口是两个点，则k=2.

例如 2D perception，在四个点的时候，有突破口。

只有一个数据点，则只有1种。有两个数据点，最多有三种dichotomies。

当有三个点时，1 dichotomy，没有违反。随便找两个点，都不能产生四种不同的情形，即没有shatter。

通俗的讲。k=2，的shatter就是 任意两个点，所有的组合情况都出现（oo，xx，ox，xo）。

同理，k=3，shatter就是不能同时出现8个点。

 

只要有k的话，说不定能让mH（N）也可能是一个多项式。

6.2 Theory of Generalization - Bounding Function - Basic Cases

我们看上限的函数，Bounding Function。是break point =k时（已知）时，最大的可能mH（N）值。

当k确认时，我们得到的一个序列中都不能出现类似k=2时的（oo，xx，ox，xo）的情形。

这样就不用对Hyposises（是positive intervals？等具体的形式）无关，只需要看B（N，3），

例如当k=1时，N去所有，都全为1，见第一列。因为只能出现全为正的情景。

而当K=N+1的那种情况，则说明break point 还要大于当前的点的数目，故值为2^N次。

而对角线的情况，则是  减 了一种情况，即 xxxxx…… 的情况。

注意，我们B（4,4）的值是15，然而对于2D perception而言，只有14种，故为严格小于。

6.3 Theory of Generalization - Bounding Function - Inductive

我们想通过建立B（4,3）和B（3，？）之间的联系。

算出的结果是11,。

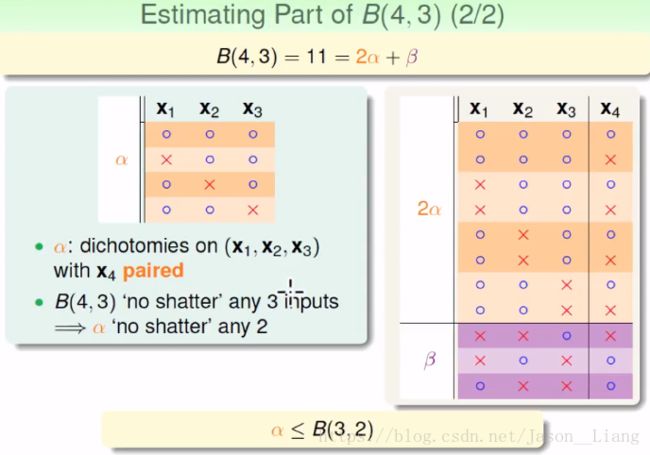
我们得到了最后的结论，mH（N）在break point 存在的情况一下，一定不会超过poly（N）

应用：我们不知道2D perceptrons 的成长函数是多少，但是我们能够知道的是，它的上线一定是（1/6）*N^3+……

6.4 Theory of Generalization - A Pictorial Pr

我们能不能把成长函数直接带入解决？答：不能。我们只能得到如下图的第二个公式的版本。

我们接下里有三个步骤，来证明这三个多余的常数。

第一个问题难点在于：Ein有限，而Eout无限，平面上有无限多条线。

我们怎么让有限多个点来区分无限多条线？我们用D'（N个点）来取代Eout.

E'in和Eout很接近，假设今天有个坏事情发生，有很大的机会，Ein和E'in隔的很远。我们就以拿来用，就可以用E'in来替代Eout。1/2的系数是用来表示是大概率发生。

我们成功的将Eout换掉了。

我们要换成有限多种，我们在乎的坏事情都只需要D和D' 有关。

我们这个平面都是数据，坏事就是一团。union bound 则是认为坏事情没有重叠。而现在我们把几乎一样的坏事情归为一点。

我们已经有固定的H了，我们想知道两次的sampling的差别。我们怎么知道两次抽样的差别？

我们最后证明出了机器学习中常用的一种公式。

总结本章的内容，我们介绍了break point，并知道了B能限制mH，知道了B的上界是poly

并且用第四节证明了mH（N）能替代M