R语言实现数据挖掘
这一周集中学习R实现的一些算法包,把一些简单的用法归结在这里,后面将继续学习。使用这些包的前提是要对算法熟悉,还好我去年看过几本算法的书,以下为总结:
1、一元线性回归
2、多元线性回归
3、Logistic回归
4、泊松回归
5、关联规则
6、决策树
7、机器集成学习
8、随机森林法则
一、一元线性回归
使用women数据框
#查看数据情况str(women)#先观察散点图,看是否可能存在线性关系
plot(women$weight,women$height)
#抽取一定的数据作为训练集和测试集
ind<-sample(2,nrow(women),replace=TRUE,prob=c(0.7,0.3))
train<-women[ind==1,]
test<-women[ind==2,]
#线性拟合
fit<-lm(weight~height,data=train)
#查看拟合的统计情况
summary(fit)
#画出散点图再加上拟合的曲线
plot(train$weight~train$height)
abline(fit)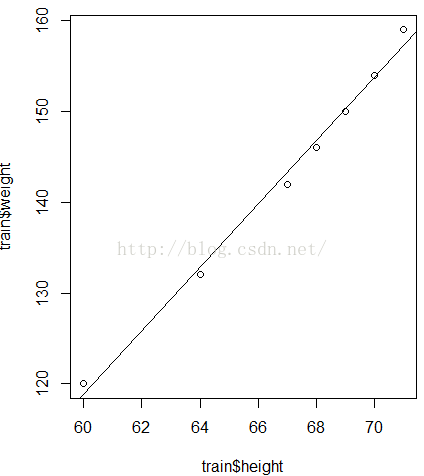
#回归诊断
library(gvlma)
gv<-gvlma(fit)
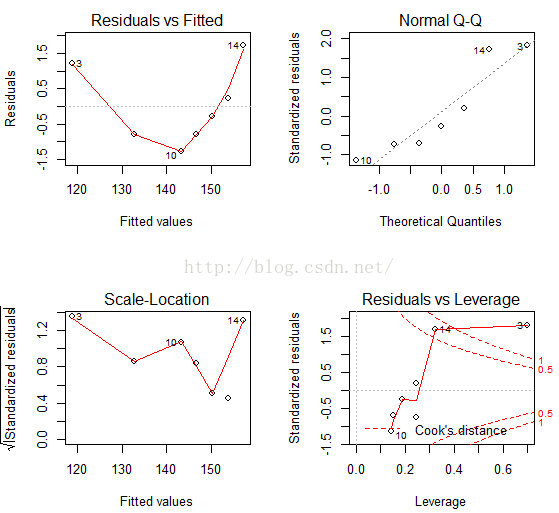
summary(gv)由回归诊断可知这次回归存在Link Function不满足条件,我们用plot(fit)来查看那个条件不满足:
由四个图可知线性、正态性以及同方差性好像都满足得不是很好,可以考虑加一个二次项:
fit2<-lm(weight~height+I(height^2),data=train)
plot(train$weight,train$height)
lines(train$weight,fitted(fit2))
opar<-par(mfrow=c(2,2))
plot(fit2)这次看上去正态性效果好,但线性和同方差性满足不到,再次用
gv2-gvlma(fit2)查看,同样发现存在假设不接受,那我们再次考虑加一个3次项拟合:
fit3<-lm(weight~height+I(height^2)+I(height^3),data=train)
Gv3<-gvlma(fit3)
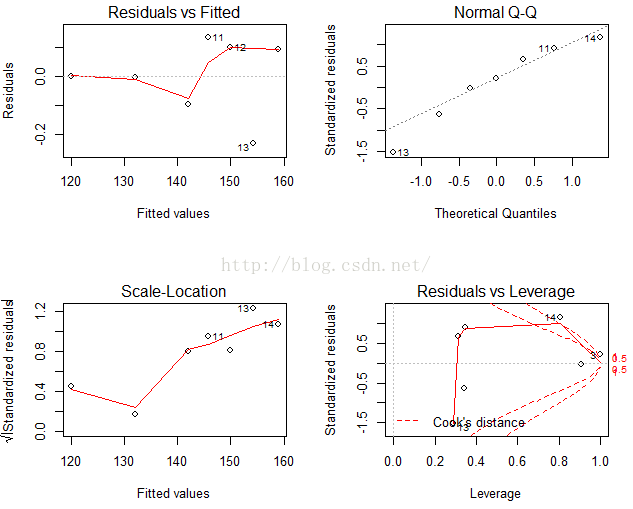
summary(gv3)这次假设都接受。
我们看看plot(fit3)
#预测
weight_pre<-predict(fit3,test)
> test$weight
[1] 115 117 123 126 129 135 139 164
画出实际和预测的图像:
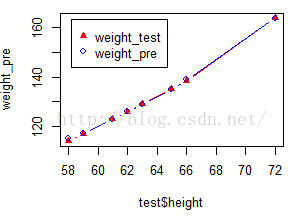
plot(test$height,weight_pre,col="red",pch=17,type="b")
lines(test$height,test$weight,col="blue",type="b")
legend("topleft",col=c("red","blue"),pch=c(17,1),legend = c("weight_test","weight_pre"),inset = .05)数据也吻合得较好。但从实际问题角度分析,重量是身高的3次多项式,这个具体的意义怎么解释?
二、多元线性回归
使用state.x77数据集x<-state.x77[,c("Murder","Population","Income","Illiteracy","Frost")]
x<-as.data.frame(x)
fit<-lm(Murder~Population+Income+Illiteracy+Frost,data=x)
gv<-gvlma(fit)
summary(gv)可以看到所有假设都可以接受,再看看summary(fit)
由结果可知,Income、Frost的显著性都不高,可以考虑去掉这两个后重新试一次。
fit2<-lm(Murder~Population+Illiteracy,data=x)
gv2<-gvlma(fit2)
summary(gv2)可以看到这次所有假设也都接受,再看看summary(fit)也都符合条件,再看看plot(fit)
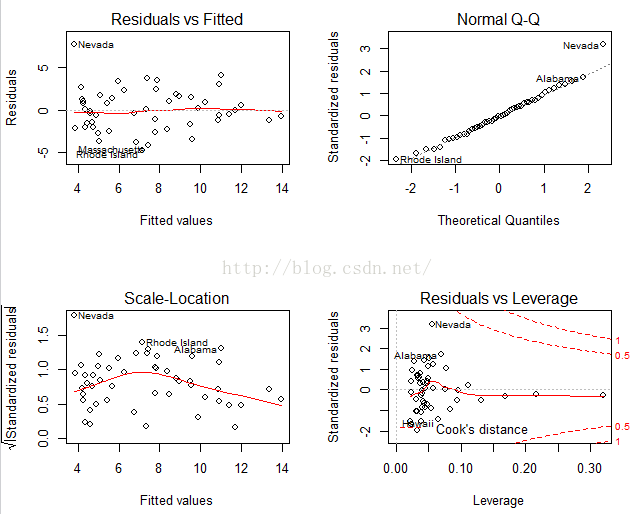
有图可知假设条件确实都满足较好。
由coef()函数读取系数
由此可得:
Murder=0.0002241861*Population+4.0807366362*Illiteracy+1.6515497424
三、Logistic回归
#数据准备
data(Affairs,package ="AER")
x<-Affairs
str(x)
summary(x)#数据抽样
x$affairs[x$affairs==0]<-0
x$affairs[x$affairs>0]<-1
x$affairs<-factor(x$affairs,levels = c(0,1),labels =c("no","yes") )
ind<-sample(2,nrow(x),replace=TRUE,prob=c(0.7,0.3))
train<-x[ind==1,]
test<-x[ind==2,]#训练数据
fit<-glm(affairs~gender+age+yearsmarried+children+religiousness+education+occupation+rating,data=train,family = binomial())
summary(fit)#由此可知affairs可能与gender,children,education,occupation没有关系,所以可以考虑去掉这几项重新训练
fit2<-glm(affairs~age+yearsmarried+religiousness+rating,data=train,family = binomial())
summary(fit2)#预测数据
pre<-predict(fit2,test)
pre=exp(pre)/(1+exp(pre))
pre[pre<0.5]<-0
pre[pre>0.5]<-1
pre<-factor(pre,levels = c(0,1),labels=c("no","yes"))
z0<-table(pre,test$affairs)#计算正确率
E0<-(sum(z0)-sum(diag(z0)))/sum(z0)
Q0<-1-E0#探究各个变量对结果概率的影响
testdata<-data.frame(rating=c(1,2,3,4,5),age=mean(train$age),yearsmarried=mean(train$yearsmarried) ,religiousness=mean(train$religiousness))
testdata$prob<-predict(fit2,newdata = testdata,type="response")#数据准备
data(Affairs,package ="AER")
x<-Affairs
str(x)
summary(x)#数据抽样
ind<-sample(2,nrow(x),replace=TRUE,prob=c(0.7,0.3))
train<-x[ind==1,]
test<-x[ind==2,]#训练数据
fit<-glm(affairs~age+yearsmarried+religiousness+rating,data=train,family =poisson(link="log"))
summary(fit)#发现age可能需要去掉
fit2<-glm(affairs~yearsmarried+religiousness+rating,data=train,family =poisson(link="log"))
summary(fit2)#预测数据
pre<-predict(fit2,test)#预测的是平均计数---r
pre<-round(exp(pre),0)#数据准备
library(arules)
groceries<-read.transactions("https://raw.githubusercontent.com/TigerInnovate/PredictiveModeling/master/groceries.csv",format="basket",sep=",")
x<-groceries
summary(x)#抽样数据-----不需要抽样数据,没有训练集,只是发现规则而不是预测。
rules<-apriori(x,parameter=list(support=0.01,confidience=0.5,minlen=2))#查看规则
inspect(rules)#按提升度排序
rules<-sort(rules,by="lift")#挑选提升度大于3的规则
myrules<-inspect(rules)
myrules<-myrules[myrules$lift>3,]#数据准备
library(rpart)
library(rpart.plot)
data("iris")
x<-iris
summary(x)#数据抽样
ind<-sample(2,nrow(x),replace=TRUE,prob=c(0.7,0.3))
train<-x[ind==1,]
test<-x[ind==2,]#建立树模型
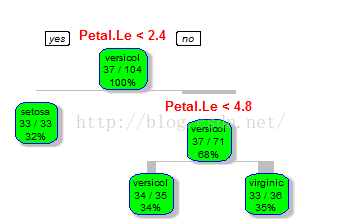
tree<-rpart(Species~.,data=train,method="class")#画出树模型
rpart.plot(tree)
rpart.plot(tree, branch=1, branch.type=2, type=1, extra=102,
shadow.col="gray", box.col="green",
border.col="blue", split.col="red",
split.cex=1.2, main="Kyphosis决策树");#查看cp和xerror
printcp(tree)#预测
pre<-predict(tree,test,type='class')
z0<-table(pre,test$Species)#计算错误率
E0<-(sum(z0)-sum(diag(z0)))/sum(z0)#数据准备
library(adabag)
data("iris")
x<-iris
summary(x)#数据抽样
ind<-sample(2,nrow(x),replace=TRUE,prob=c(0.7,0.3))
train<-x[ind==1,]
test<-x[ind==2,]#boosting学习
boost<-boosting(Species~.,data=train)
summary(boost)#预测
pre<-predict(boost,test,type="class")
#可以直接由预测结果得出预测的效果,错误率为0.04761905
#baging学习
bag<-bagging(Species~.,data=train)
summary(bag)#预测
pre<-predict(bag,test,type="class")#可以直接由预测结果得出预测的效果,错误率为 0.07142857,由此可知boosting的效果比baging的效果要好
barplot(bag$importance)#画出变量的重要性比较
b<-errorevol(bag,iris)#计算全体的误差演变
plot(b$error,type="l",main="AdaBoost error vs number of trees") #对误差演变进行画图
八、随机森林法则
#数据准备
library(randomForest)
rf<-randomForest(Species~.,data=train)
summary(rf)#预测
pre<-predict(rf,test,type="class")
Z0<-table(pre,test$Species)#计算错误率
E0<-(sum(Z0)-sum(diag(Z0)))/sum(Z0)
E0#错误率为0.04761905
#画出重要性柱图
barplot(t(rf$importance))