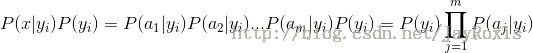“Naive”贝叶斯算法 —— 朴素贝叶斯(Naive Bayesian)算法
“Naive”贝叶斯算法 —— 朴素Bayesian算法有趣现象
你们搞的这个Naive贝叶斯啊,亦可赛艇!
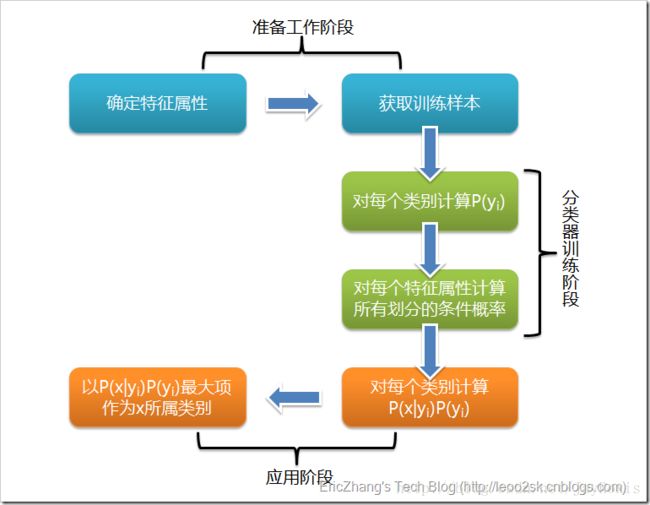
朴素贝叶斯算法原理
从统计学知识回到我们的数据分析。假如我们的分类模型样本是:
(x(1)1,x(1)2,…x(1)n,y1),(x(2)1,x(2)2,…x(2)n,y2),…(x(m)1,x(m)2,…x(m)n,yn)
(x1(1),x2(1),…xn(1),y1),(x1(2),x2(2),…xn(2),y2),…(x1(m),x2(m),…xn(m),yn)
即我们有m个样本,每个样本有n个特征,特征输出有K个类别,定义为C1,C2,…,CKC1,C2,…,CK。
从样本我们可以学习得到朴素贝叶斯的先验分布P(Y=Ck)(k=1,2,…K)P(Y=Ck)(k=1,2,…K),接着学习到条件概率分布P(X=x|Y=Ck)=P(X1=x1,X2=x2,…Xn=xn|Y=Ck)P(X=x|Y=Ck)=P(X1=x1,X2=x2,…Xn=xn|Y=Ck),然后我们就可以用贝叶斯公式得到X和Y的联合分布P(X,Y)了。联合分布P(X,Y)定义为:
P(X,Y=Ck)=P(Y=Ck)P(X=x|Y=Ck)=P(Y=Ck)P(X1=x1,X2=x2,…Xn=xn|Y=Ck)(1)(2)
(1)P(X,Y=Ck)=P(Y=Ck)P(X=x|Y=Ck)(2)=P(Y=Ck)P(X1=x1,X2=x2,…Xn=xn|Y=Ck)
从上面的式子可以看出P(Y=Ck)P(Y=Ck)比较容易通过最大似然法求出,得到的P(Y=Ck)P(Y=Ck)就是类别CkCk在训练集里面出现的频数。但是P(X1=x1,X2=x2,…Xn=xn|Y=Ck)P(X1=x1,X2=x2,…Xn=xn|Y=Ck)很难求出,这是一个超级复杂的有n个维度的条件分布。朴素贝叶斯模型在这里做了一个大胆的假设,即X的n个维度之间相互独立,这样就可以得出:
P(X1=x1,X2=x2,…Xn=xn|Y=Ck)=P(X1=x1|Y=Ck)P(X2=x2|Y=Ck)…P(Xn=xn|Y=Ck)
P(X1=x1,X2=x2,…Xn=xn|Y=Ck)=P(X1=x1|Y=Ck)P(X2=x2|Y=Ck)…P(Xn=xn|Y=Ck)
从上式可以看出,这个很难的条件分布大大的简化了,但是这也可能带来预测的不准确性。你会说如果我的特征之间非常不独立怎么办?如果真是非常不独立的话,那就尽量不要使用朴素贝叶斯模型了,考虑使用其他的分类方法比较好。但是一般情况下,样本的特征之间独立这个条件的确是弱成立的,尤其是数据量非常大的时候。虽然我们牺牲了准确性,但是得到的好处是模型的条件分布的计算大大简化了,这就是贝叶斯模型的选择。
@T2噬菌体
最后回到我们要解决的问题,我们的问题是给定测试集的一个新样本特征(x(test)1,x(test)2,…x(test)n(x1(test),x2(test),…xn(test),我们如何判断它属于哪个类型?既然是贝叶斯模型,当然是后验概率最大化来判断分类了。我们只要计算出所有的K个条件概率P(Y=Ck|X=X(test))P(Y=Ck|X=X(test)),然后找出最大的条件概率对应的类别,这就是朴素贝叶斯的预测了。
为了让本文更“专业”“学术”些,以上是从一些网页摘的大神解释,感到头晕的同学直接看第二章,有兴趣的可以去看原文。
以上解释的原文链接:http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html
Naive Bayesian为什么说是“Naive”
朴素贝叶斯算法简称NB算法,现在还有各种变种,通常用的时候还会加入拉普拉斯修正。都叫NB算法了,关于其牛逼的地方就不多说了。
这个算法这几天盯着它的定义总觉得有问题存在,最近做了几个例子更加发现了其不足之处。
朴素贝叶斯算法在统计概率的原理上分析应该是对目标进行最可能的判决,但是真的没有问题吗。事实上,看过这个算法定义的人应该明白其中的一个步骤把“属于分类y的一个事件是待预测事件x”的概率(也叫作“分类y中观测到x的概率”)展开成了“属于分类y中的一个事件有a属性”的概率乘积。这里的“属于分类y中的一个事件有a属性”的概率即:
![]()
如果各属性独立,即通俗理解各个输入的参数间不会相互有关联。比如酒的品质来说,酒的酒精度和pH值作为两个输入参数来预测酒的品质,利用贝叶斯模型,就需要假设这酒精度和pH值两个特征无关。那么用公式表示:
下面问题来了:
对于很多的分类问题,两个输入参量之间往往会有联系。就像酒的酒精度往往会影响酒的pH值,人的身高和体重也往往有关联。
举个栗子
那么,基于各属性间相互独立的朴素贝叶斯算法会有什么样的问题呢?
我们以下面这个问题为例:
比马印第安人糖尿病问题
比马印第安人糖尿病数据集(Pima Indians Diabetes
Dataset)涉及根据医疗记录预测比马印第安人5年内糖尿病的发病情况。它是一个二元分类问题。每个类的观察值数量不均等。一共有 768 个观察值,8个输入变量和1个输出变量。缺失值通常用零值编码。变量名如下:
- 怀孕次数
- 口服葡萄糖耐受试验中, 2小时的血浆葡萄糖浓度。
- 舒张压(mm Hg)
- 三头肌皮肤褶层厚度(mm)
- 2小时血清胰岛素含量(μU/ml)
- 体重指数(体重,kg /(身高,m)^ 2)
- 糖尿病家族史
- 年龄(岁)
类变量(0 或 1),代表患有/未患有糖尿病。数据集下载地址:http://t.cn/RfaFfq8
以上的几个参数中,先不说其他的,就年龄而言,和其它参数有显著的关联。关于这个问题,预测最普遍类的基准性能是约 65% 的分类准确率,最佳结果达到约 77% 的分类准确率。
概率论基础解释
在一个样本空间内,对于一个样本的n个特性,可能会有其相关性。在对输入特征向量的处理中,就可以通过PCA(主成分分析)的方式来进行去关联化,同时达到了去冗余和对输入空间降维的作用。
整个NB网络对非关联性太过自信,在实测中,朴素贝叶斯网络的准确度呈现十分低的准确度,也是这样。
关于贝叶斯网络的研究和其MSMR改进或权重改进算法后续会涉及。