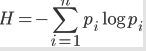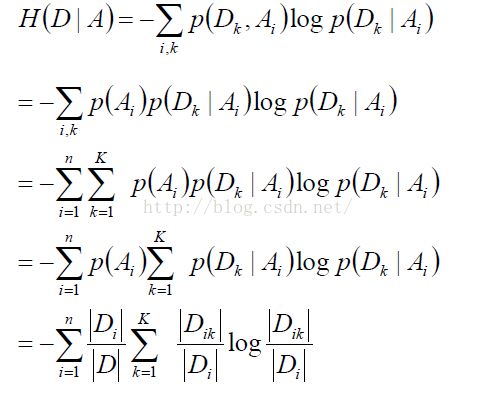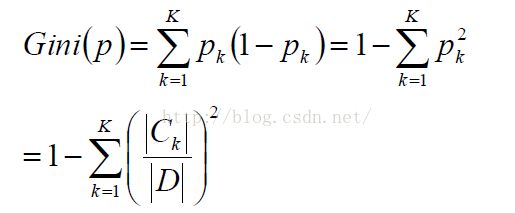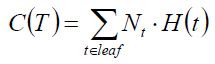机器学习之决策树（Decision Tree）&随机森林（Random forest）

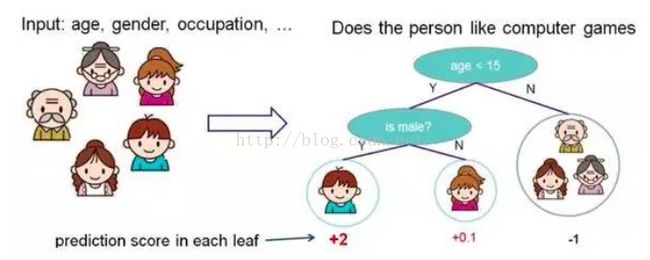
决策树是机器学习中最接近人类思考问题的过程的一种算法，通过若干个节点，对特征进行提问并分类（可以是二分类也可以使多分类），直至最后生成叶节点（也就是只剩下一种属性），下面这张图形象表示了决策树的过程：

而随机森林是基于决策树过拟合提出的基于多个弱分类器vote投票的方式的一种集成学习算法.

1. Decision tree 结构：1个根节点+多干内部节点和叶节点，根节点和若干内部节点是判断模块，用来判断对特征怎样分类，叶节点是终止模块，到这里决策树就完成了分类过程.

2.决策树之三部曲：

feature selection+Decision tree生成（递归过程）+pruing（剪枝，防止过拟合）

3.决策树分支节点划分原则：纯度原则（Purity），分支节点的样本尽可能属于同一类，也就是纯度越高越好

判断纯度引入数学参数：信息熵用来描述信息的不确定度，信息熵越大，信息越不确定，包含的可能性就越大

其公式为：

因此决策树的分支的原则是让熵最终越小越好，这样就要求在每次分支的时候信息增益是最大的，这样熵减小的就快，收敛快，直到最终熵最小，完成分类.

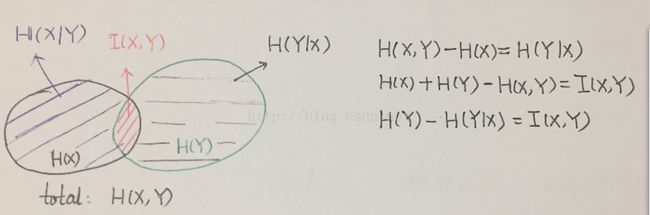
这里引入信息论中的熵 H(X),联合熵 H(X,Y),条件熵 H(X|Y),互信息 I(X,Y) 的概念，四者关系简单如下图：

4.决策树之三种算法：

一、信息增益：ID3

定义为:对于特征A的信息增益为：g(D,A)=H(D)-H(D|A),从上图看出，信息增益就是给定训练集D时，特征A和训练集D的互信息I(D,A).选取信息增益最大的特征作为分支的节点.

其中，条件熵H(D|A)的计算公式如下：

信息增益的缺点：对数目较多的属性有偏好，且生成额决策树层次多，深度浅，为改善这些问题，提出方法二.

二、信息增益率：C4.5

其等于信息增益/属性A的熵

信息增益率的缺点：对数目较少的属性有偏好，后又有方法三.

三、CART基尼指数：

其计算公式如下：

Gini系数可以理解为y=-lnx在x=1处的一阶展开.

总结之，一个属性的信息增益（率）/gini指数越大，表明属性对样本的熵较少的程度越大，那么这个属性使得样本从不确定性变为确定性的能力越强，分支时选择该属性作为判断模块使得决策树生成的越快.

5.决策树之防止过拟合(Overfitting)

一、剪枝：

引入评价函数（损失函数）：所有叶节点的加权求熵，其值越小表明分类越精准，那么该决策树分类觉越好.Nt是叶节点中样本的个数.

剪枝方法之预剪枝：

从前往后生成树的过程中，从树根开始，逐一生成节点，比较其生成与不生成的C(T），在验证集上选择C(T)小的作为最终的数.

剪枝方法之后剪枝：

剪枝系数：

决策树生成后，查找剪枝系数最小的节点，视为一颗决策树，重复以上，知道只剩下一个节点，这样得到多颗决策树，在验证集上计算损失函数最小的那棵树作为最终的决策树.

二、随机森林（Random forest）：生成多颗决策树，投票选举的原则

引入两种方法：bootstrapping（有放回的随机抽取）和bagging（bootstrap aggragation）

bagging的方法如下：

随机森林是在bagging上做了改进，计算过程如下：

注意：随机森林或者bagging是基于若干个弱分类器组成的基本分类器进行vote决定最终的分类的，基本分类器也可以选择强分类器（如LR,SVM等），但可能因为强分类器某些特征太多明显而不能被多个分类器的平均抹掉，不能很好达到过拟合的效果.

6.决策树之优缺点：

上述将决策树介绍了，其优缺点如下：

优点：

->计算简单，易理解，可解释性强

->适合处理确实属性的样本，对样本的类别要求不高（可以是数值，布尔，文本等混合样本）

->能处理不相干特征

缺点：

->容易过拟合

->忽略了数据之间的相关性

->不支持在线学习，对新样本，决策树需要全部重建

7.决策树算法实践:

代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor

if __name__ == "__main__":
    n = 500
    x = np.random.rand(n) * 8 - 3
    x.sort()
    y = np.cos(x) + np.sin(x) + np.random.randn(n) *  0.4
    x = x.reshape(-1, 1)

    reg = DecisionTreeRegressor(criterion='mse')
    reg1 = RandomForestRegressor(criterion='mse')
    dt = reg.fit(x, y)
    dt1 = reg1.fit(x, y)
    x_test = np.linspace(-3, 5, 100).reshape(-1, 1)
    y_hat = dt.predict(x_test)
    plt.figure(facecolor="w")
    plt.plot(x,y,'ro',label="actual")
    plt.plot(x_test,y_hat,'k*',label="predict")
    plt.legend(loc="best")
    plt.title(u'Decision Tree', fontsize=17)
    plt.tight_layout()
    plt.grid()
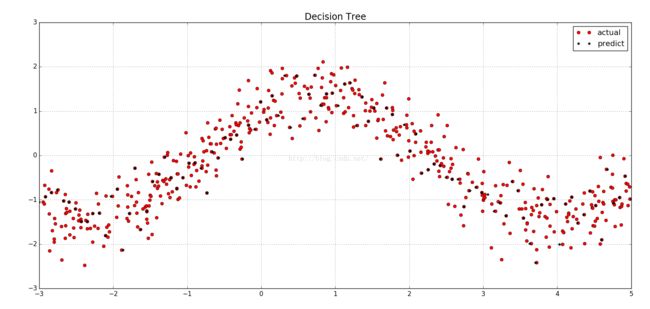
    plt.show()

图实现decision tree：

总结：decision tree分类器和改进其overfitting的随机森林分类器，在应用上是OK的，在学术上就不那么高大上了~~毕竟没有复杂的数学推导等.

熵相关参考：

http://blog.csdn.net/kxy_tech/article/details/3993457