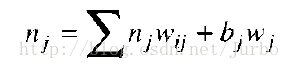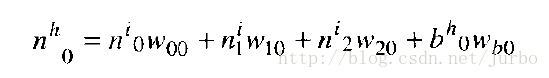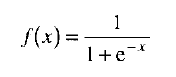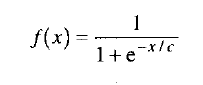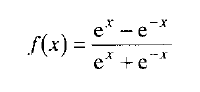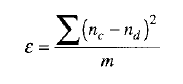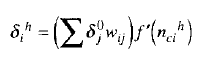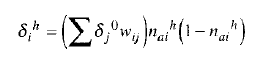游戏开发中的人工智能(十四):神经网络
接上文 游戏开发中的人工智能(十三):不确定状态下的决策:贝叶斯技术
本文内容:“神经网络”技术让游戏具有学习和适应的能力。事实上,从决策判断到预测玩家的行为,都可以应用。我们会详谈最广泛使用的神经网络结构(三层前馈神经网络)。
神经网络
人工神经网络(artificial neural network,即ANN),简称神经网络(neural network,即NN),是一种模仿生物神经网络的结构和功能的数学模型或计算模型。神经网络由大量的节点(或称神经元)之间相互联接构成。每个节点代表一种特定的输出函数,称为激励函数(activation function)。每两个节点间的连接都代表一个对于通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。网络的输出则依网络的连接方式,权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达。
神经网络在游戏中的优点和缺点
人工神经网络的特点和优越性,主要表现在三个方面:
第一,具有自学习功能。例如实现图像识别时,只在先把许多不同的图像样板和对应的应识别的结果输入人工神经网络,网络就会通过自学习功能,慢慢学会识别类似的图像。自学习功能对于预测有特别重要的意义。预期未来的人工神经网络计算机将为人类提供经济预测、市场预测、效益预测,其应用前途是很远大的。
第二,具有联想存储功能。用人工神经网络的反馈网络就可以实现这种联想。
第三,具有高速寻找优化解的能力。寻找一个复杂问题的优化解,往往需要很大的计算量,利用一个针对某问题而设计的反馈型人工神经网络,发挥计算机的高速运算能力,可能很快找到优化解。
尽管有这些优点,神经网络在游戏中的应用还是有限的。下面有两个关键因素。
首先神经网络具有“非线性”的特征,这使运算过程难以控制,也让测试人员不知所措。其次,神经网络也具有“非常定性”的特征,即神经网络具有自适应、自组织、自学习能力。神经网络会产生什么样的输出结果,通常也难以预测。这两个因素让神经网络的测试和调试变得异常困难。
分析三层前馈神经网络
结构
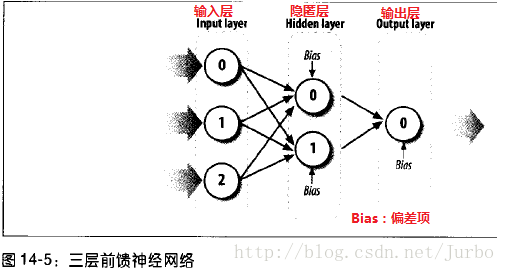
本章的焦点是三层前馈神经网络。图14-5 显示了这种网络的基本结构。
三层前馈神经网络由输入层、隐匿层、输出层组成。每一层的神经元数目不限。输入层的每个神经元,都和隐匿层的每个神经元相连接。隐匿层的每个神经元,都和输出层的每个神经元相连接。此外,除了输入层之外,每个神经元还有一个额外的输入值叫做偏差项(bias)。图14-5 中的数字代表三层中的每个节点。当我们用公式计算每个神经元的值时,就会用到此数字编号。
计算三层前馈神经网络的输出值。先从提供给每个输入层神经元的输入值开始。接着,权衡这些输入值后,传给隐匿层的神经元。接着重复此过程,从隐匿层传给输出层。也就是说,隐匿层神经元的输出值,变成输出层的输入值。从输入层到隐匿层再到输出层的过程,就是前馈流程。
输入层
神经网路的输入数据显然非常重要,没有输入数据,神经网络就不可能进行运算。
怎样选择输入数据?需要提供多少输入数据?
把什么数据当做输入数据应该根据问题而定。要看所要解决的问题是什么,而且选择什么样的游戏参数、数据和环境特征值,对要解决的任务而言都有很大的影响。
如果把输入神经元的数量控制在最少,训练神经网络的工作就会大为简化。在某些情况下,要选择的输入数据是什么,不见得可以一目了然。就此而言,通用的做法就是把你认为可能重要的数据,当做输入数据。然后,让神经网络自行弄清楚哪些才是重要的。面对所需输出的结果,神经网络擅长排列输入数据间的相对重要性。
通常,你可以合并或者转换重要信息,改成某种比较简洁的形式,借此减少输入数据的数量。
举个例子,假设你试着用神经网络,控制游戏中宇宙飞船登录星球事件。宇宙飞船的质量是变量,除了其他因素之外,该星球的重力加速度也是重要因素,应该将之视为输入数据,提供给神经网络。如果我们为每个参数都建立一个输入神经元,一个给质量,另一个给重力加速度。然而,这种做法会迫使神经网络增加额外的工作:弄清宇宙飞船的质量和星球的重力加速度之间的关系。比较好的输入方式是,把这两个重要参数合并成一个神经元,即将宇宙飞船的重力,作为输入神经元,即质量和重力加速度的乘积。
输入数据的形式是什么?
你可以以各种形式的数据,作为神经网络的输入数据。对于游戏而言,这类输入数据通常有三种类型组成:布尔、枚举以及连续类型。神经网络以实数为对象,所以,无论你有什么数据类型,都必须先转换成适当的实数,才能作为输入数据。
举个例子。如果是布尔值时,我们不能把 ture 或 false 传给神经网络的输入节点。我们要以 1.0 表示 true,而以 0.0 表示 false。如果输入数据是枚举类型。例如,假设你设计的神经网络是为了对敌人进行分类,而其中的一个考虑因素是所使用的武器种类。武器种类选项可能是像是短剑、劣质剑、长剑、刀、十字弓、短弓或长弓。这里的先后次序不重要,而我们假定这些可能性是互斥的。一般而言,在神经网络里处理这种数据,用的是所谓的“n分之一”的编码方法。基本而言,我们替每种可能性都建立一个输入值,然后根据每个特定的可能性是否为 true,把输入值设为 1.0 或 0.0(false)。例如,如果敌人持有刀,则输入向量为 {0,0,0,1,0,0,0},1 就是刀这个输入节点的值,而0 是其他可能节点的值。
权重
人工神经网络里的权重,就好像生物神经网络里的突触连接。(突触是指一个神经元的冲动传到另一个神经元或传到另一细胞间的相互接触的结构)。因此每两个神经元之间必然有突触,即人工神经网络里,神经元和另一神经元的连接都有相匹配的权重。
权重会影响特定输入数据的强度,可以抑制或激活神经网络的行为。实际上可以说,是权重在决定神经网络的行为。求出权重的任务,是训练神经网络或让神经网络演化的主题。
神经元的总输入值,是每个输入值和该神经元相连的权重,乘以自身的输入值的总和,再加上偏差项。下列方程式是特定神经元 j 的总输入值,就是从 i 个神经元的一组输入值计算而得来的。
我们看一个简单的例子。假设你想计算图14-5 隐匿层中第0个神经元的总输入值。利用上述公式,我们可以得到隐匿层第0个神经元的总输入值的公式:
在此公式中,n 代表神经元的值。就输入神经元而言,这些就是输入值。就隐匿神经元而言,就是指总输入值。上标 h 和 i 代表的神经元所属的层次,h 指隐匿层,i 指输入层。下标指的是每一层的节点。
我们注意到,某特定神经元的总输入值只是其他神经元加权后输入值的线性组合。如果是这样,神经网络怎么像我们前面提到的那样,逼近高度非线性函数呢?关键在于总输入值如何转换成某神经元的输出层。明确地将,激励函数(activation function,或译为 活化函数、激发函数)把总输入值以非线性方式对应到响应的输出值。
活化(激励)函数
活化函数可以接受神经元的总输入值,予以处理,再产生神经元的输出结果。活化函数应该是非线性的(除了稍后会谈到的一种特例之外)。如果活化函数不为非线性,则神经网络就会降低为线性函数的线性组合,其设计就无法逼近非线性函数及非线性关系。
logistic(罗吉斯)函数
最常用的活化函数是 logistic(罗吉斯)函数,或称为 S型函数(sigmoid function)。图14-6 就是 S型函数。
logistic 函数的公式如下:
有时候,这个函数也会写成:
就此而言,c 用来改变函数的形状,也就是说,沿着水平轴伸缩函数。
注意,输入值是水平轴,对所有 x 值而言,此函数的输出值都介于 0~1 之间。实际上,可用的范围是 0.1~0.9 。0.1 左右的值,表示神经元没有被活化,而0.9 左右的值表示神经元被活化。注意一点,无论 x 值多大(正或负),logistic 函数永远不会达到 1.0 或 0.0 ,logistic 函数只能渐进这两个值。如果你试着训练神经网络时,起始值对特定输出神经元给予的值是 1.0 ,则永远也得不到结果。比较合理的值是 0.9,锁定此值,会让训练速度加快许多。如果试着训练神经网络,使其输出的值是 0 ,则此时应该用 0.1 左右的值。
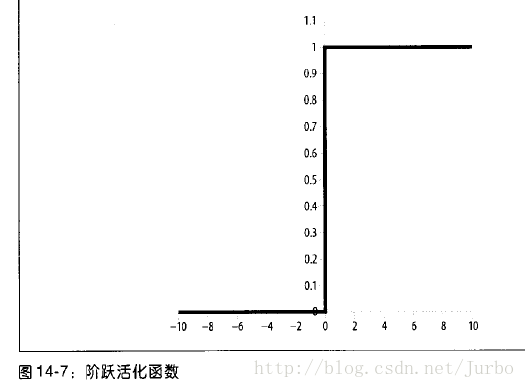
阶跃函数
阶跃函数如图14-7 所示。
阶跃函数的公式如下:
阶跃函数用于早期神经网络发展时期,但由于缺少导数(无法微分),难以训练神经网络。
双曲正切函数
双曲正切函数如图 14-8 所示。
双曲正切函数的公式如下:
双曲正切函数偶尔会用到,目的是加快训练神经网络。一般而言,logistic 函数似乎是最广为使用的。
线性活化函数
图14-9 显示的是有时会用到的另一个活化函数,称为线性活化函数。
线性活化函数的公式就是:f(x)= x
这就是说,神经元的输出值就是总输入值,即所有与之相连的输入神经元的加权输入值的总和,再加上偏差项。
偏差项
谈到如何计算神经元总输入值时,我们曾提到除了输入层之外,每个神经元还有一个额外的输入值叫做偏差项(bias)。这个偏差项就是每个神经元的偏差值和偏差权重,前面所述的神经元总输入值计算公式中,已经表现出来,公式如下所示:
bj 是偏差值,而 wj 是偏差权重。
基本而言,偏差项是把总输入值沿着活化函数的水平轴移动,有效改变神经元活化的阀值。偏差值总是设为 1 或 -1,而偏差权重则经有训练神经网络中调整,如同其他权重那样。
输出层
就像输入层那样,你替网络选择的输出神经元,也和所需解决的问题有关。一般而言,最好把输出神经元数量保持最少,以减少计算和训练时间。
设想一个神经网络,给定输入值后,想让输出结果用来分类输入值。也许你想判断一组特定输入值是否落入某类型内。就此而言,你可以使用一个输出神经元。如果该神经元受到活化,则结果为 ture(即落在某类型内),如果没有受到活化,则结果为 false(即没有落在某类型内)。如果用 logistic 函数做输出活化运算。0.9 左右的输出值表示受到活化,结果为 true。而 0.1 左右的输出值表示没受到活化,结果为 false。实际上,也许无法刚好得到 0.9 或 0.1 的输出值。例如,也许得到 0.78 或 0.31。因此,必须定义一个阀值,以便评估输出值是否表示活化。一般而言,可以直接在两极值间,选一个输出阀值。就 logistic 函数而言,可以用 0.5。如果输出值大于 0.5,则结果就是受到 活化或 true,否则就是 false。
当你感兴趣的是某类输入值,是否落在多种类型中的其中一种时,就可以使用一个以上的输出神经元。每一种类型都有一个输出神经元。就这类输出形式而言,假定高输出值指的是受到活化,而低输出值指的是没受到活化。每个节点的实际输出值,可以包含在某范围之内,置于是什么范围,就和神经网络是如何训练,神经网络所用的输出活化函数的种类有关了。有了一组输出值,以及每个输出节点的结果,其中一种了解输出值是否活化的方式,就是找出拥有最高输出值的神经元。这就是所谓的“赢家通吃”(winner-take-all)法。有最高活化值的神经元就是最后所得的类型。本章后面会举一个用此法的实例。
隐匿层
到目前为止,我们讨论了输入神经元、输出神经元,还有如何替神经元计算总输入值。但还没有专门讨论隐匿层。在三层前馈神经网路中,有一层神经元放在隐匿层里,夹在输入层和输出层之间。
如图14-5 所示,每个输出神经元都和隐匿神经元连接在一起。而且,每个隐匿神经元会把其输出传到每个输出层的神经元中。顺带一提,神经网络并不是只有三层前馈这种结构,还有其他各种各样的形式,比如有一个以上的隐匿层、回馈层、以及完全没有隐匿层。然而,三层前馈神经网络是最常用的一种形态。无论如何,隐匿层是网络处理输入数据的特征所不可或缺的。隐匿层神经元越多,网络能处理的特征就越多,隐匿层神经元越少,网络能处理的特征就越少。
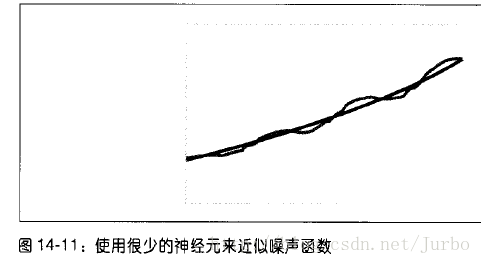
那么所谓的特征是什么?为了了解这个特征的含义,可以把神经网络当做函数的近似值的方式来思考。假设有一个函数,如图14-10 所示,噪声很多。
训练神经网络来近似噪声很多的函数时,如果使用很少的隐匿层神经元时,可能会得到如图14-11 所示的结果。
如图14-11 所示,近似的函数有捕捉输入数据的趋势,但漏掉了各处噪声的特征。特定应用情况下,究竟多少隐匿神经元才适当,很难固定。一般而言,要用试误法来决定。如果你的三层网络不是用于自动联想,隐匿层的适当数量,大约等于输入和输出神经元数量乘积的平方根。
记住一点,碰上CPU用量很大的游戏时,隐匿层神经元数量越多,计算网络输出值的时间就越长。因此,应该试着把隐匿层神经元数量缩减到最小。
训练神经网络
本质上,训练神经网络就是一个最佳化过程,在这个过程里,你试着找出最佳权重值,让神经网络能产生合适的输出。
训练方式可以分为两类:指导训练以及无指导训练。这里只讨论指导训练法中最常用的一种:倒传递法。
倒传递训练
重申一次,训练的目标是找出连接所有神经元之值的权重,让输入值可以产生所需的输出值。为了达到此目的,你需要一个训练数据集,由输入数据和对应该输入数据所要的输出值组成。下一步是利用某些技术的其中一种,不断重复地替整个网络找出一组权重值,使得该神经网络可以产生符合训练数据集内,每组数据所要的输出结果。做好之后,就可以让网络启动,提供不再训练数据集内的新数据,使其产生合理的输出结果。
因为训练是一种最佳化的过程,我们需要用某种方法做最优化。就倒传递法而言,是实施试误法,把误差最小化。有了输入值以及产生的输出值后,必须将产生的输出值和已知想要的输出值做比较,量化两结果间的吻合度。例如,算出误差。有很多误差的算法可用,这里用最常见的:均方误差,也就是计算所得的输出值,和想要的输出值之间的差值的平方的平均数。
因为要把误差最小化,以得出最佳的权重,必须对函数进行微分。明确地讲,我们必须对活化函数微分,而这就是为什么 logistic 函数非常好用的原因所在,我们可以轻易求出其导数。
如前所述,找出最佳权重是个不断重复的过程。如下所示
- 准备一个训练数据集,包含输入数据和相对应的所希望的输出值
- 替神经网络的权重设初始值,设成某些随机的较小的数值
- 把每组输入数据输入给神经网络,算出输出值
- 比较算出的输入值和所希望的输出值,算出误差
- 调整权重以减小误差,再重复上述过程。
步骤1~3 后面的实例中会看到。这里,我们先细谈步骤4~5。
计算误差
要训练神经网络,你得给出一组输入数据,使其产生某些输出。要根据某组输入值比较计算所得到的输出值和所希望的输出值时,必须计算其误差。这样不但可以确认计算所得的输出值是对是错,也可以确认其对错的程度。最常用的误差计算方法就是均方误差,即所希望的输出值和计算的输出值之间的差值的平方的平均值:
在此公式中,ε 是此训练数据集的均方误差。nc 和 nd 分别是计算所得的输出值和所希望的输出值,也就是所有输出神经元之值,而 m 是每轮的输出神经元的数量。
我们的目标是,通过不断调整神经网络中连接所有神经元的权重值,使误差值尽可能小到在实际中可行。要知道权重需做多大调整,每轮进行时,也必须算出输出层和隐匿层中,每个神经元的误差。
计算输出神经元误差的公式如下:
使用 logistic 函数的导数重写此公式后,计算输出神经元误差的公式如下:
计算隐匿层神经元误差的公式:
注意,这里每个隐匿层神经元的误差,是该隐匿神经元连接的每个输出层神经元的误差乘以连接关系上的权重值的函数。也就是说,要计算隐匿层神经元的误差并依序调整权重,你必须从输出层往回走向输入层。
注意到,这里再次需要用到活化函数的导数。假设还是用 logistic 活化函数。使用 logistic 函数的导数重写此公式后,计算隐匿神经元误差的公式如下:
最后一点,输入层没有所谓的误差,因为输入神经元的值是我们给定的。
调整权重
算出误差后,可以继续算出神经网络中每个权重要做的适当校正值。每个权重的校正值如下。
记住一点,每个权重都有校正值,而且校正值各不相同。更新连接输出神经元和隐匿神经元之间的权重时,由输出神经元的误差及其值来计算权重的校正值。当更新连接隐匿层神经元和输入层神经元之间的权重时,则用隐匿层神经元的误差及其值。
学习率是个常数,影响每个权重,要被调整的多少,通常设成小值,比如 0.25 或 0.5 。折是你必须调整的几个参数之一。如果设的太高,权重的最佳化也许会过头,但如果设的太低,训练神经网络可能得花较长的时间。
增加动量
我们可以对刚才谈过的权重校正值做一点修改。修改技巧名叫增加动量。我们在谈怎么增加动量之前,先讨论为何要增加动量。
在任何通用最佳化过程中,目标不是最小化就是最大化某个函数。更明确地讲,我们感兴趣的是在某个输入参数的范围内,找出特定函数整体的最小值或最大值。很多问题都会在函数中展现出来,例如局部的最小值或最大值,即函数的谷和峰。如图14-12 所示。
此例中,这个函数在图中的范围内,有整体最小值和最大值。此外,还有好几个局部最小值和最大值,由小谷小峰表示。
我们感兴趣的是如何把神经网络的误差最小化。明确地讲,是找出最佳权重,使其产生整体最小误差。然而,也许会得到局部最小误差,而不是整体最小误差。
当我们开始训练神经网络时,我们把权重设成某些随机小值。此时,我们不知道这些随机小值和最佳权重有多接近。因此,也许在设初值的时候,权重比较接近局部最小值,而不是整体最小值。
更新权重的一种方法是梯度下降法,也就是用函数的导数,试着取得最小值。不过问题是,我们不知道得到的最小值是整体最小值还是局部最小值。
在神经网络中,我们用动量法解决这种问题。动量法,并没有去掉局部最小值的可能性,但这种方法有助于远离局部最小值,而往整体最小值靠近。基本而言,我们要在权重校正值中再加上一个小值,也就是前一轮中,权重校正值的函数。这样会给权重校正值一个动力,如果逼近的是局部最小值,这样的算法也许可以跳过局部最小值,往整体最小值靠近。
所以,用上增加动量的技巧后,计算权重校正值的新公式如下所示:
编写神经网络的类
下面几节是两个实现三层前馈神经网络的 C++类。本章稍后会看一个利用这几个类的实例。如果你想先知道这个神经网络的运行过程,再看其内部细节,可先跳到“用神经网络解决追逐和闪躲之决策”那一节。
我们为三层前馈神经网络实现两个类。第一个类代表的是通用层次类,可用作输入层、隐匿层和输出层。第二个类代表由这三层组成的整个神经网络。
通用层次类 NeuralNetworkLayer
NeuralNetworkLayer 实现了多层前馈网络中的通用层,负责处理该层内的所包含的神经元。其执行的任务包括,配置和释放存储神经元之值、误差和权重的内存、对权重赋初值、计算神经元的值以及调整权重。
例14-1 是该类的开头的内容。
//例14-1:NeuralNetworkLayer 类
class NeuralNetworkLayer
{
public:
int NumberOfNodes;
int NumberOfChildNodes;
int NumberOfParentNodes;
double** Weights;
double** WeightChanges;
double* NeuronValues;
double* DesiredValues;
double* Errors;
double* BiasWeights;
double* BiasValues;
double LearningRate;
bool LinearOutput;
bool UseMomentum;
double MomentumFactor;
NeuralNetworkLayer* ParentLayer;
NeuralNetworkLayer* ChildLayer;
NeuralNetworkLayer();
void Initialize(int NumNodes, NeuralNetworkLayer* parent, NeuralNetworkLayer* child);
void CleanUp(void);
void RandomizeWeights(void);
void CalculateErrors(void);
void AdjustWeights(void);
void CalculateNeuronValues(void);
};层次之间彼此的连接方式是采用上下关系。例如,输入层是隐匿层的上层,而隐匿层是输出层的上层。此外,输出层是隐匿层的下层,而隐匿层是输入层的下层。注意,输入层没有上层,而输出层也没有下层。
这个类的成员主要是由数组组成,用来储存神经元权重、值,误差以及偏差项等。此外,还有一些成员含有一些设定值,控制此层的行为。成员如下所示:
NumberOfNodes:存储的是层次类实体中,神经元(或者说节点)的数量
NumberOfChildNodes:存储的是层次类实体中,位于下层神经元的数量
NubmerOfParentNodes:存储的是层次类实体中,位于上层神经元的数量
Weights:指向下层神经元的二维权重数组
WeightsChanges:双精度二维数组,将校正值存储在此数组中
NeuronValues:存储该层神经元计算所得的值(或活化值)
DesiredValues:存储该层神经元的目标值,我们会根据 NeuronValues 和 DesiredValues 来计算误差
Errors:存储该层中,和每个神经元相关的误差
BiasWeights:存储的是该层中和每个神经元相连接的偏差权重值
BiasValues:存储该层中和每个神经元相连接的偏差值
LearningRate:存储的是学习率,用来计算权重校正值
LinearOutput:指出此层的神经元是否使用线性活化函数,只有该层是输出层时才能用。false 则改用 logistic 活化函数。默认值为 false。
UseMomentum:布尔值,指出调整权重值时是否使用动量。默认值是 false
MomentumFactor:动量系数。如果 UseMomentum 是 true,才会用到这个变量
ParentLayer:指向代表此层上层 NeuralNetworkLayer 实体的指针。对输入层来说,此指针设为 NULL
ChildLayer:指向代表此层下层 NeuralNetworkLayer 实体的指针。对输出层来说,此指针设为 NULL
NeuralNetworkLayer 类包含 7 个方法。我们逐一详谈,先从 构造方法开始。
NeuralNetworkLayer( )
//例14-2:NeuralNetworkLayer类的构造方法
NeuralNetworkLayer::NeuralNetworkLayer()
{
ParentLayer = NULL;
ChildLayer = NULL;
LinearOutput = false;
UseMomentum = false;
MomentumFactor = 0.9;
}Initialize( )
//例14-3:Initialize()
void NeuralNetworkLayer::Initialize(int NumNodes, NeuralNetworkLayer* parent, NeuralNetworkLayer* child)
{
int i, j;
// 配置内存
NeuronValues = (double*) malloc(sizeof(double) * NumberOfNodes);
DesiredValues = (double*) malloc(sizeof(double) * NumberOfNodes);
Errors = (double*) malloc(sizeof(double) * NumberOfNodes);
if(parent != NULL)
{
ParentLayer = parent;
}
if(child != NULL)
{
ChildLayer = child;
Weights = (double**) malloc(sizeof(double*) * NumberOfNodes);
WeightChanges = (double**) malloc(sizeof(double*) * NumberOfNodes);
for(i = 0; idouble*) malloc(sizeof(double) * NumberOfChildNodes);
WeightChanges[i] = (double*) malloc(sizeof(double) * NumberOfChildNodes);
}
BiasValues = (double*) malloc(sizeof(double) * NumberOfChildNodes);
BiasWeights = (double*) malloc(sizeof(double) * NumberOfChildNodes);
}
else
{
Weights = NULL;
BiasValues = NULL;
BiasWeights = NULL;
}
// 确定全部为0
for(i=0; i0;
DesiredValues[i] = 0;
Errors[i] = 0;
if(ChildLayer != NULL)
for(j=0; j0;
WeightChanges[i][j] = 0;
}
}
//指定偏差值和权重的初值
if(ChildLayer != NULL)
for(j=0; j1;
BiasWeights[j] = 0;
}
} Initialize( ) 方法是替那些动态数组(指针的指针)配置内存,以便存储该层内神经元的权重、值、误差以及偏差值和偏差权重值。此外,还替这些数组赋初值。
这个方法有三个参数:该层的神经元数量,指向上层的指针以及指向下层的指针。如果该层是输入层,则上层指针之处应传递 NULL。如果该层是输出层,则下层指针之处应传递 NULL。
此方法开头,NeuronValues、DesiredValues 和 Errors 数组的内存都会被配置好。这几个数组都是一维数组,元素个数由该层神经元数量决定。
接着,设定上下层指针。如果下层指针是NULL,则此层为输入层或隐匿层,而且必须配置相连接的权重的内存。因为 Weights 和 WeightChanges 是二维数组,我们必须分步骤配置内存。第一步是配置内存,存储 double 类型数组的指针,其元素个数则由该层神经元数量决定。接着,对每一个元素,也要配置内存,存储实际数组值,个数由下层的节点数决定。输入层或隐匿层的每个神经元,都和其相关的下层内的每个神经元相连接。因此,权重数组Weights 和权重校正值数组WeightChanges 的总量,就等于该层内神经元的数量,乘以下层内的神经元数量。
我们还要配置 偏差值和偏差权重值数组的内存,其总量等于相连接的下层的神经元数量。
内存配置好之后,再来替数组赋初值。除了将偏差值数组设为-1 或 +1 之外,其他数组的值都为0。
CleanUp( )
CleanUp( ) 负责把 Initialize() 分配的内存释放掉。
//例14-4:CleanUp()
void NeuralNetworkLayer::CleanUp(void)
{
int i;
free(NeuronValues);
free(DesiredValues);
free(Errors);
if(Weights != NULL)
{
for(i = 0; ifree(Weights[i]);
free(WeightChanges[i]);
}
free(Weights);
free(WeightChanges);
}
if(BiasValues != NULL) free(BiasValues);
if(BiasWeights != NULL) free(BiasWeights);
}
RandomizeWeights( )
前面我们提过,神经网络的权重在一开始要初始化成某些随机小值,才能开始训练神经网络。例14-5 的 RandomizeWeights( ) 方法替我们将权重初始化成某些小值。
//例14-5:RandomizeWeights()
void NeuralNetworkLayer::RandomizeWeights(void)
{
int i,j;
int min = 0;
int max = 200;
int number;
srand( (unsigned)time( NULL ) );
for(i=0; ifor(j=0; jabs(rand())%(max-min+1))+min));
if(number>max)
number = max;
if(number<min)
number = min;
Weights[i][j] = number / 100.0f - 1;
}
}
for(j=0; jabs(rand())%(max-min+1))+min));
if(number>max)
number = max;
if(number<min)
number = min;
BiasWeights[j] = number / 100.0f - 1;
}
} 在这个函数中,替 Weights 数组中,每个元素在 -1 和 +1 之间随机选取数。BiasWeights 数组中的偏差权重也是如此。开始训练前才会调用此方法,将权重初始随机化。
CalculateErrors( )
CalculateErrors( ) 使用先前讨论过的公式计算出每个神经元的误差。
//例14-7:CalculateErrors()
void NeuralNetworkLayer::CalculateErrors(void)
{
int i, j;
double sum;
if(ChildLayer == NULL) // output layer
{
for(i=0; i1.0f - NeuronValues[i]);
}
}
else if(ParentLayer == NULL)
{
// input layer
for(i=0; i0.0f;
}
}
else
{
// hidden layer
for(i=0; isum = 0;
for(j=0; jsum += ChildLayer->Errors[j] * Weights[i][j];
}
Errors[i] = sum * NeuronValues[i] * (1.0f - NeuronValues[i]);
}
}
} 如果该层没有下层,也就是该层为输出层时,要用计算输出层误差的公式。如果该层没有上层,也就是该层为输入层时,要把误差设为0。如果该层同时有上下层,则其为隐匿层,要使用隐匿层的误差计算公式。
AdjustWeights( )
AdjustWeights( ) 负责计算每个相连权重的校正值。
//例14-8:AdjustWeights()
void NeuralNetworkLayer::AdjustWeights(void)
{
int i, j;
double dw;
if(ChildLayer != NULL)
{
for(i=0; ifor(j=0; jErrors[j] * NeuronValues[i];
Weights[i][j] += dw + MomentumFactor * WeightChanges[i][j];
WeightChanges[i][j] = dw;
}
}
for(j=0; jErrors[j] * BiasValues[j];
}
}
} 如果该层为输入层或隐匿层,即该层有下层,权重必须调整。
嵌套 for 循环绕行该层以及下层的节点。每层中的每个神经元都和下层的每一个节点相连接。在这些嵌套循环中,权重校正值的计算运用前述公式。如果增加动量,则动量系数乘以上一轮权重校正值,也会加入此权重校正值内。然后,此轮的权重校正值会存到 WeightChanges 数组内,以供下一轮使用。如果没有增加动量,则权重校正值就不会加上动量,也就没有必要存储权重校正值。
最后,偏差权重也以类似连接权重的调整方式来调整。就每个和子节点相连的偏差权重而言,其校正值就是学习率乘以下层神经元误差,再乘以偏差值。
CalculateNeuronValues( )
CalculateNeuronValues( ) 利用神经元总输入值和活化函数的公式,计算该层内每个神经元的活化值。如例14-6 所示。
//例14-6:CalculateNeuronValues()
void NeuralNetworkLayer::CalculateNeuronValues(void)
{
int i,j;
double x;
if(ParentLayer != NULL)
{
for(j=0; j0;
for(i=0; iNeuronValues[i] * ParentLayer->Weights[i][j];
}
x += ParentLayer->BiasValues[j] * ParentLayer->BiasWeights[j];
if((ChildLayer == NULL) && LinearOutput)
NeuronValues[j] = x;
else
NeuronValues[j] = 1.0f/(1+exp(-x));
}
}
} j 循环绕行下层节点,i 循环绕行上行节点。在这些嵌套循环中,总输入值会算出来,存储在 x 变量内。该层中每个节点的总输入值,是上层(i循环)的所有和每个 j 节点相连之值的加权总和,再加上 j 节点的加权偏差值。
算出每个节点的总输入值后,可以利用活化函数算出每个神经元的值。每一层都是用 logistic 函数,但输出层除外。因为要根据 LinearOutput 布尔值来决定是否使用线性活化函数。
代表整个神经网络的类 NeuralNetwork
NeuralNetwork 类包括三个 NeuralNetworkLayer 类的实体,分别是神经网络中的每一层:输入层、隐匿层以及输出层。例14-9 是此类开头的内容。
//例14-9:NeuralNetwork 类
class NeuralNetwork
{
public:
NeuralNetworkLayer InputLayer;
NeuralNetworkLayer HiddenLayer;
NeuralNetworkLayer OutputLayer;
void Initialize(int nNodesInput, int nNodesHidden, int nNodesOutput);
void CleanUp();
void SetInput(int i, double value);
double GetOutput(int i);
void SetDesiredOutput(int i, double value);
void FeedForward(void);
void BackPropagate(void);
int GetMaxOutputID(void);
double CalculateError(void);
void SetLearningRate(double rate);
void SetLinearOutput(bool useLinear);
void SetMomentum(bool useMomentum, double factor);
void DumpData(char* filename);
};这个类只有三个成员,对应三个层次实体。然而,这个类有13个方法。我们要逐一说明。
Initialize( )
//例14-10:Initialize()
void NeuralNetwork::Initialize(int nNodesInput, int nNodesHidden, int nNodesOutput)
{
InputLayer.NumberOfNodes = nNodesInput;
InputLayer.NumberOfChildNodes = nNodesHidden;
InputLayer.NumberOfParentNodes = 0;
InputLayer.Initialize(nNodesInput, NULL, &HiddenLayer);
InputLayer.RandomizeWeights();
HiddenLayer.NumberOfNodes = nNodesHidden;
HiddenLayer.NumberOfChildNodes = nNodesOutput;
HiddenLayer.NumberOfParentNodes = nNodesInput;
HiddenLayer.Initialize(nNodesHidden, &InputLayer, &OutputLayer);
HiddenLayer.RandomizeWeights();
OutputLayer.NumberOfNodes = nNodesOutput;
OutputLayer.NumberOfChildNodes = 0;
OutputLayer.NumberOfParentNodes = nNodesHidden;
OutputLayer.Initialize(nNodesOutput, &HiddenLayer, NULL);
}Initialize() 带三个参数,分别对应构成此神经网络三个层次的每一层中所含的神经元数量。这些参数用来对输入层、隐匿层以及输出层的层次类实体做初始化。
Initialize() 也会把层次间正确的上下关系连接做好,接着,替连接的权重值赋随机值。
CleanUp( )
CleanUp( ) 方法调用每个层次实体的 CleanUp( ) 方法。
//例14-11:CleanUp()
void NeuralNetwork::CleanUp()
{
InputLayer.CleanUp();
HiddenLayer.CleanUp();
OutputLayer.CleanUp();
}SetInput( )
SetInput( ) 用来设定特定输入神经元的输入值。
//例14-12:SetInput()
void NeuralNetwork::SetInput(int i, double value)
{
if((i>=0) && (ivalue;
}
} SetInput( ) 带两个参数,对应需要设定输入值的神经元的索引值,以及输入值本身。然后,会设定特定的输入值。这个方法会在两个地方被调用。一是在训练时要设定训练数据集的输入数据,而是神经网络实际运用时,要设定输入数据,使输出值能被计算出来。
GetOutput( )
一旦神经网络产生一些输出值,我们要以某种方式获得。
//例14-13:GetOutput()
double NeuralNetwork::GetOutput(int i)
{
if((i>=0) && (ireturn OutputLayer.NeuronValues[i];
}
return (double) INT_MAX; // 指出错误
} GetOutput() 带一个参数,即想要获得其输出值的输出神经元的索引值。这个方法会返回指定的输出神经元的活化值。如果你指定的索引值,不再有效输出神经元范围之内,则会返回 INT_MAX 表示错误。
SetDesiredOutput( )
训练神经网络期间,我们必须比较计算所得的输出值以及所希望的输出值。SetDesiredOutput( ) 方法可以根据某组输入值,指定需要的输出值。
//例14-14:SetDesiredOutput()
void NeuralNetwork::SetDesiredOutput(int i, double value)
{
if((i>=0) && (ivalue;
}
} SetDesiredOutput( ) 带两个参数,对应要设定所想要的输出值的输出神经元的索引值,以及所想要的输出值本身。
FeedForward( )
为了实际让神经网络能根据一组输入值来产生输出,我们要调用 例14-15的 FeedForward( )。
//例14-15:FeedForward()
void NeuralNetwork::FeedForward(void)
{
InputLayer.CalculateNeuronValues();
HiddenLayer.CalculateNeuronValues();
OutputLayer.CalculateNeuronValues();
}这个方法依次调用输入层、隐匿层、输出层的 CalculateNeuronValues( ) 方法。一旦这些调用都执行完后,输出层将包含计算所得的输出值。
BackPropagate( )
训练神经网络期间,一旦输出值被算出后,我们必须利用倒传递技巧,调整连接的权重值。如例14-6 所示。
//例14-6:BackPropagate()
void NeuralNetwork::BackPropagate(void)
{
OutputLayer.CalculateErrors();
HiddenLayer.CalculateErrors();
HiddenLayer.AdjustWeights();
InputLayer.AdjustWeights();
}BackPropagate( ) 首先调用输出层和隐匿层的 CalculateErrors( ) 方法,输出层在前,然后是隐匿层。接着,调用隐匿层和输入层的 AdjustWeights( ) 方法,隐匿层在前,然后是输入层。这里的顺序很重要,也就是说我们倒着经过神经网络。
GetMaxOutputID( )
当你使用的网络有好几个输出神经元时,我们需要采用“赢家通吃”求出被活化的输出神经元。即,找出输出值最高的输出神经元。如例14-17 所示。
//例14-17:GetMaxOutputID()
int NeuralNetwork::GetMaxOutputID(void)
{
int i, id;
double maxval;
maxval = OutputLayer.NeuronValues[0];
id = 0;
for(i=1; i.NumberOfNodes; i++)
{
if(OutputLayer.NeuronValues[i] > maxval)
{
maxval = OutputLayer.NeuronValues[i];
id = i;
}
}
return id;
} GetMaxOutputID( ) 绕行输出层的所有神经元,找出有最高输出值的神经元,然后返回拥有最高值神经元的索引值。
CalculateError( )
CalculateError( ) 用来计算某组输出值的误差,如例14-18 所示。
//例14-18:CalculateError()
double NeuralNetwork::CalculateError(void)
{
int i;
double error = 0;
for(i=0; ierror += pow(OutputLayer.NeuronValues[i] - OutputLayer.DesiredValues[i], 2);
}
error = error / OutputLayer.NumberOfNodes;
return error;
} CalculateError( ) 会利用先前讨论过的均方误差公式,计算所得输出值和想要的输出值之间的误差。
SetLearningRate( )
SetLearningRate( ) 用来设定神经网络中每层的学习率,如例14-19 所示。
//例14-19:SetLearningRate()
void NeuralNetwork::SetLearningRate(double rate)
{
InputLayer.LearningRate = rate;
HiddenLayer.LearningRate = rate;
OutputLayer.LearningRate = rate;
} SetLinearOutput( )
SetLinearOutput( ) 用来替神经网络中的每一层设定 LinearOutput 布尔值。此实例中,只有输出层会用到线性活化函数。如例14-20 所示。
//例14-20:SetLinearOutput()
void NeuralNetwork::SetLinearOutput(bool useLinear)
{
InputLayer.LinearOutput = useLinear;
HiddenLayer.LinearOutput = useLinear;
OutputLayer.LinearOutput = useLinear;
}SetMomentum( )
SetMomentum( ) 用来设定 UseMomentum 布尔值以及神经网络中每一层的动量系数。如例14-21 所示。
//例14-21:SetMomentum()
void NeuralNetwork::SetMomentum(bool useMomentum, double factor)
{
InputLayer.UseMomentum = useMomentum;
HiddenLayer.UseMomentum = useMomentum;
OutputLayer.UseMomentum = useMomentum;
InputLayer.MomentumFactor = factor;
HiddenLayer.MomentumFactor = factor;
OutputLayer.MomentumFactor = factor;
}DumpData( )
DumpData( ) 用来把神经网络中的某些重要数据放到某个输出文件中。如例14-22 所示。
//例14-22:DumpData()
void NeuralNetwork::DumpData(char* filename)
{
FILE* f;
int i, j;
f = fopen(filename, "w");
fprintf(f, "--------------------------------------------------------\n");
fprintf(f, "Input Layer\n");
fprintf(f, "--------------------------------------------------------\n");
fprintf(f, "\n");
fprintf(f, "Node Values:\n");
fprintf(f, "\n");
for(i=0; ifprintf(f, "(%d) = %f\n", i, InputLayer.NeuronValues[i]);
fprintf(f, "\n");
fprintf(f, "Weights:\n");
fprintf(f, "\n");
for(i=0; ifor(j=0; jfprintf(f, "(%d, %d) = %f\n", i, j, InputLayer.Weights[i][j]);
fprintf(f, "\n");
fprintf(f, "Bias Weights:\n");
fprintf(f, "\n");
for(j=0; jfprintf(f, "(%d) = %f\n", j, InputLayer.BiasWeights[j]);
fprintf(f, "\n");
fprintf(f, "\n");
fprintf(f, "--------------------------------------------------------\n");
fprintf(f, "Hidden Layer\n");
fprintf(f, "--------------------------------------------------------\n");
fprintf(f, "\n");
fprintf(f, "Weights:\n");
fprintf(f, "\n");
for(i=0; ifor(j=0; jfprintf(f, "(%d, %d) = %f\n", i, j, HiddenLayer.Weights[i][j]);
fprintf(f, "\n");
fprintf(f, "Bias Weights:\n");
fprintf(f, "\n");
for(j=0; jfprintf(f, "(%d) = %f\n", j, HiddenLayer.BiasWeights[j]);
fprintf(f, "\n");
fprintf(f, "\n");
fprintf(f, "--------------------------------------------------------\n");
fprintf(f, "Output Layer\n");
fprintf(f, "--------------------------------------------------------\n");
fprintf(f, "\n");
fprintf(f, "Node Values:\n");
fprintf(f, "\n");
for(i=0; ifprintf(f, "(%d) = %f\n", i, OutputLayer.NeuronValues[i]);
fprintf(f, "\n");
fclose(f);
} 用神经网络解决追逐和闪躲之决策
本章要讨论的范例是第四章中已经讨论过的群聚和追逐的范例,只不过做了一些修改。
那一章我们讨论的是一群单位追逐玩家所控制的单位。此例做的修改是,计算机控制的单位改用神经网络,决定是否追逐或闪躲玩家,或者和其他计算机控制单位聚在一起。
下面说明实例如何运作。大约有20个计算机控制的单位在屏幕上移动,会攻击玩家、逃离玩家或者和其他计算机控制单位聚在一起。要采取什么行为,是由神经网络做决策。当计算机控制单位和玩家处在战斗距离内时,就会发生“战斗”,会减掉容许击中次数。容许击中次数变为0时,就会“死掉”,然后自动“重生”。
我们希望能看见计算机控制单位,学会在和玩家对战毫无胜算时,避开玩家。相反的,我们希望计算机控制单位,学习到它们的玩家对手很弱时,变得比较有攻击性。
初始化以及训练
利用第四章的群聚实例作为起点,必须做的第一件事,就是新增一个全局变量 TheBrain,来表示神经网络,如例14-23 所示。
//例14-23:新全局变量
NeuralNetwork TheBrain;程序开始时,必须对神经网络做初始化,包括神经网络的配置和训练。Initialize( ) 函数中有新增的代码,实现这部分功能,如例14-24 所示。
//例14-24:初始化
bool Initialize(void)
{
int i;
…
for(i=0; i<_MAX_NUM_UNITS; i++)
{
…
Units[i].HitPoints = _MAXHITPOINTS;
Units[i].Chase = false;
Units[i].Flock = false;
Units[i].Evade = false;
Units[i].Wander = true;
}
…
Units[0].HitPoints = _MAXHITPOINTS;
…
TheBrain.Initialize(4, 3, 3/*4*/);
TheBrain.SetLearningRate(0.2);
TheBrain.SetMomentum(true, 0.9);
TrainTheBrain();
return true;
}我们还需要替刚体结构新增一些成员,如例14-25 所示。新的成员包括容许击中的次数,以及指出该单位是否在追逐、闪躲或群聚的布尔值。
//例14-25:RigidBody2D 类
class RigidBody2D {
public:
…
double HitPoints;
int NumFridens;
int Command;
bool Chase;
bool Flock;
bool Evade;
bool Wander;
double Inputs[4];
};我们也加了一个 Inputs 向量。当用神经网络决定该单位要采取什么行动时,就可以存储输入值。
回到例14-24 的 Initialize( ) 方法中,当单位都初始设定好之后。要做的第一件事是调用 Initialize( ) 方法设定神经网络,传递代表每层神经元数量的值。就此例而言,我们有四个输入神经元、三个隐匿神经元以及三个输出神经元。这个网络类似图14-4 的图示。
下一件事就是把学习率设成 0.2,然后调用 SetMomentum( ) 方法,表示我们想在训练时使用动量,再把动量系数设为 0.9。
现在,神经网络已经初始设定好了。可以调用 TrainTheBrain( ) 函数加以训练。如例14-26 所示。
//例14-26:TrainTheBrain()
void TrainTheBrain(void)
{
int i;
double error = 1;
int c = 0;
TheBrain.DumpData("PreTraining.txt");
while((error > 0.05) && (c<50000))
{
error = 0;
c++;
for(i=0; i<14; i++)
{
TheBrain.SetInput(0, TrainingSet[i][0]);
TheBrain.SetInput(1, TrainingSet[i][1]);
TheBrain.SetInput(2, TrainingSet[i][2]);
TheBrain.SetInput(3, TrainingSet[i][3]);
TheBrain.SetDesiredOutput(0, TrainingSet[i][4]);
TheBrain.SetDesiredOutput(1, TrainingSet[i][5]);
TheBrain.SetDesiredOutput(2, TrainingSet[i][6]);
//TheBrain.SetDesiredOutput(3, TrainingSet[i][7]);
TheBrain.FeedForward();
error += TheBrain.CalculateError();
TheBrain.BackPropagate();
}
error = error / 14.0f;
}
//c = c * 1;
TheBrain.DumpData("PostTraining.txt");
}开始训练网络之前,先把神经网络的数据放到某个文字文件中。这样,调试时才能予以参考。接着,进入一个 while 循环,使用倒传递算法训练神经网络。while 循环会一直运行,直到计算的误差小于某指定值,或者直到循环次数达到指定的最大阀值。后者的情况是避免 while 循环,因为误差标准达不到而永远循环。
具体讲 while 循环之前,先看用来训练神经网络的训练数据。名为 TrainingSet 的全局数组用来存储训练数据。如例14-27 所示。
//例14-27:训练资料
double TrainingSet[14][7] = {
//友军,容许击中次数,敌人是否交战,距离,追逐,群聚,闪躲
0, 1, 0, 0.2, 0.9, 0.1, 0.1,
0, 1, 1, 0.2, 0.9, 0.1, 0.1,
0, 1, 0, 0.8, 0.1, 0.1, 0.1,
0.1, 0.5, 0, 0.2, 0.9, 0.1, 0.1,
0, 0.25, 1, 0.5, 0.1, 0.9, 0.1,
0, 0.2, 1, 0.2, 0.1, 0.1, 0.9,
0.3, 0.2, 0, 0.2, 0.9, 0.1, 0.1,
0, 0.2, 0, 0.3, 0.1, 0.9, 0.1,
0, 1, 0, 0.2, 0.1, 0.9, 0.1,
0, 1, 1, 0.6, 0.1, 0.1, 0.1,
0, 1, 0, 0.8, 0.1, 0.9, 0.1,
0.1, 0.2, 0, 0.2, 0.1, 0.1, 0.9,
0, 0.25, 1, 0.5, 0.1, 0.1, 0.9,
0, 0.6, 0, 0.2, 0.1, 0.1, 0.9
};训练数据中包含14组输入和输出值,每组数据有四个代表该单位的友军数量、其容许击中次数、敌人是否交战以及和敌人之间距离的输入节点。此外,还有三个输出节点的数据,对应追逐、群聚和闪躲的行为。
注意,所有数据值都位于 0.0~1.0 之间。作为输出值,要得到 0.0 或 1.0 是不切实际的。所以我们以 0.1 表示无活化,而以 0.9 表示活化。注意到,这些输出值代表的理想输出值。
回到例14-26,处理倒传递训练的 while 循环里。进入 while 循环时,误差设成 0。就每组数据而言,要设定输入神经元的值以及所想要的输出神经元的值,然后调用神经网络的 FeedForward( ) 方法。之后,计算误差调用 CalculateError( ) 方法,在误差变量中累加结果。接着,调用 BackPropagete( ) 方法调整连接的权重值。就一轮循环而言,这些步骤都完成后,就能求出这一轮的均方误差。
训练完成后,神经网络的数据会被放到某个文字文件中,以备稍后使用。
例14-28 的 UpdateSimulation( ) 函数是第四章讨论过的UpdateSimulation( ) 函数的修改版。这里只列出修改部分。
//例14-28:修改后的UpdateSimulation()
void UpdateSimulation(void)
{
…
int i;
Vector u;
bool kill = false;
…
// 计算当前和目标物正在交战的敌军单位数量
Vector d;
Units[0].NumFriends = 0;
for(i=1; i<_MAX_NUM_UNITS; i++)
{
d = Units[i].vPosition - Units[0].vPosition;
if(d.Magnitude() <= (Units[0].fLength * _CRITICAL_RADIUS_FACTOR))
Units[0].NumFriends++;
}
// 减少目标物的容许击中次数
if(Units[0].NumFriends > 0)
{
Units[0].HitPoints -= 0.2 * Units[0].NumFriends;
if(Units[0].HitPoints < 0)
{
Units[0].vPosition.x = _WINWIDTH/2;
Units[0].vPosition.y = _WINHEIGHT/2;
Units[0].HitPoints = _MAXHITPOINTS;
kill = true;
}
}
else
{
//Units[0].HitPoints += 1;
//if(Units[0].HitPoints > _MAXHITPOINTS) Units[0].HitPoints = _MAXHITPOINTS;
}
// 更新计算机控制单位
for(i=1; i<_MAX_NUM_UNITS; i++)
{
u = Units[0].vPosition - Units[i].vPosition;
if(kill)
{
if((u.Magnitude() <= (Units[0].fLength * _CRITICAL_RADIUS_FACTOR)) /*&& (Units[i].Command != 2)*/)
{
ReTrainTheBrain(i, 0.9, 0.1, 0.1, 0.1);
Units[i].HitPoints += _MAXHITPOINTS/4.0f;
if(Units[i].HitPoints > _MAXHITPOINTS) Units[i].HitPoints = _MAXHITPOINTS;
}
}
// 处理单位的容许击中次数
if(u.Magnitude() <= (Units[0].fLength * _CRITICAL_RADIUS_FACTOR))
{
Units[i].HitPoints -= DamageRate;
if((Units[i].HitPoints < 0))
{
Units[i].vPosition.x = GetRandomNumber(_WINWIDTH/2-_SPAWN_AREA_R, _WINWIDTH/2+_SPAWN_AREA_R, false);
Units[i].vPosition.y = GetRandomNumber(_WINHEIGHT/2-_SPAWN_AREA_R, _WINHEIGHT/2+_SPAWN_AREA_R, false);
Units[i].HitPoints = _MAXHITPOINTS/2.0;
// if(Units[i].Command == 0)
ReTrainTheBrain(i, 0.1, 0.1, 0.9, 0.1);
}
}
else
{
Units[i].HitPoints+=0.01;
if(Units[i].HitPoints > _MAXHITPOINTS) Units[i].HitPoints = _MAXHITPOINTS;
/* if((Units[i].HitPoints < 0))
{
Units[i].vPosition.x = GetRandomNumber(_WINWIDTH/2-_SPAWN_AREA_R, _WINWIDTH/2+_SPAWN_AREA_R, false);
Units[i].vPosition.y = GetRandomNumber(_WINHEIGHT/2-_SPAWN_AREA_R, _WINHEIGHT/2+_SPAWN_AREA_R, false);
Units[i].HitPoints = _MAXHITPOINTS/2;
if (Units[i].Command != 0)
ReTrainTheBrain(i, 0.9, 0.1, 0.1, 0.1);
}*/
}
// 取得新命令
Units[i].Inputs[0] = Units[i].NumFriends/_MAX_NUM_UNITS;
Units[i].Inputs[1] = (double) (Units[i].HitPoints/_MAXHITPOINTS);
Units[i].Inputs[2] = (Units[0].NumFriends>0 ? 1:0);
Units[i].Inputs[3] = (u.Magnitude()/800.0f);
TheBrain.SetInput(0, Units[i].Inputs[0]);
TheBrain.SetInput(1, Units[i].Inputs[1]);
TheBrain.SetInput(2, Units[i].Inputs[2]);
TheBrain.SetInput(3, Units[i].Inputs[3]);
TheBrain.FeedForward();
Units[i].Command = TheBrain.GetMaxOutputID();
switch(Units[i].Command)
{
case 0:
Units[i].Chase = true;
Units[i].Flock = false;
Units[i].Evade = false;
Units[i].Wander = false;
break;
case 1:
Units[i].Chase = false;
Units[i].Flock = true;
Units[i].Evade = false;
Units[i].Wander = false;
break;
case 2:
Units[i].Chase = false;
Units[i].Flock = false;
Units[i].Evade = true;
Units[i].Wander = false;
break;
/*case 3:
Units[i].Chase = false;
Units[i].Flock = false;
Units[i].Evade = true;
Units[i].Wander = true;
break;*/
}
DoUnitAI(i);
…
} // i 循环结束
kill = false;
…
}这个修改过的 UpdateSimulation( ) 函数,所做的第一件事就是,计算当前正和目标物交战的计算机控制单位数量。就我们这个例子来说,如果某单位和目标物处在指定距离内,就被视为和目标物正在交战。
一旦我们求出交战中单位的数量,就根据该数量的大小,按比例减去目标物的容许击中次数。如果目标物的容许击中次数变为0,则目标物就视为“死亡”,并在屏幕的中央“重生”。此时,kill 布尔值也会设为 true。
下一步是处理计算机控制单位。就此工作来说,我们进入一个 for 循环,轮流允许所有计算机控制单位。进入该循环时,计算出当前单位和目标物之间的距离。接着,检查目标物是否已死。如果是,就检查当前单位和目标物之间的位置关系,即是否在交战范围内。如果是,就重新训练神经网络以强化这种追逐行为。本质上,如果该单位和目标物交战,而目标物死了,我们强化追逐行为,使其更具攻击性。
例14-29 的 ReTrainTheBrain( ) 函数负责重新训练神经网络。
//例14-29:ReTrainTheBrain()
void ReTrainTheBrain(int i, double d0, double d1, double d2, double d3)
{
double error = 1;
int c = 0;
while((error > 0.1) && (c<5000))
{
c++;
TheBrain.SetInput(0, Units[i].Inputs[0]);
TheBrain.SetInput(1, Units[i].Inputs[1]);
TheBrain.SetInput(2, Units[i].Inputs[2]);
TheBrain.SetInput(3, Units[i].Inputs[3]);
TheBrain.SetDesiredOutput(0, d0);
TheBrain.SetDesiredOutput(1, d1);
TheBrain.SetDesiredOutput(2, d2);
//TheBrain.SetDesiredOutput(3, d3);
TheBrain.FeedForward();
error = TheBrain.CalculateError();
TheBrain.BackPropagate();
}
//c = c * 1;
}ReTrainTheBrain( ) 只是再次操作倒传递训练算法,但这次是以该单位的输入值,以及制定的目标输出值作为训练数据。
UpdateSimulation( ) 函数的下一步是处理当前单位的容许击中次数。如果当前单位处在目标物的交战范围内,就把该单位预设的容许击中次数减少。如果该单位的容许击中次数变为零,即假定其死亡,此时,就令其在随机之处重生。同时,我们训练该单位要闪躲,不要追逐。
我们要使用神经网络替该单位做决策,也就是说,在当前条件下,该单位应该追逐、群聚或闪躲。首先,要把输入值提供给神经网络。第一个输入值是当前单位的友军数量,调整成可伸缩值的方式是,除以哪些单位的最大数量。第二个输入值是该单位的容许击中次数,调整成可伸缩值的方式是,除以容许击中次数的最大值。第三个输入值是指出目标物是否在交战。如果目标物正在交战,此时就设为 1.0,反之,则设为 0.0。第四个输入值是和目标物间的距离,调整成可伸缩值的方式是,除以屏幕宽度。
所有输入值都设定好以后,再来调用 FeedForward( ) 函数传递网络。该方法调用之后,就能检视神经网络的输出值,以推导出正确的行为。就此而言,我们选择最高活化值的输出,即调用 GetMaxOutputID( ) 方法所得的结果。然后,这个 ID 值会用在 switch 语句中,替此单位设定适当的行为标号。如果 ID 为 0,则该单位追逐。如果 ID 为1,则群聚。ID 为2,则该单位闪躲。
代码下载
在VC 6++ 环境下可运行。
代码:AIDemo14-1
http://pan.baidu.com/s/1hswySRi