数组的全排列

1.问题背景

学过数学的人都知道，全排列的意思是什么。现在如何用计算机的编程语言实现数组的全排列呢？

数组的全排列可用于求解八皇后问题，具体参见：全排列解决八皇后问题。与此同时，全排列经常会出现在笔试或者面试，如求字符串的全排列。之所以那它作为考题，因为它难度适中，既可以考察递归实现，又能进一步考察非递归的实现，便于区分出考生的水平。所以，掌握它很重要。

2.全排列的递归实现

2.1求解思路

全排列表示把集合中元素的所有按照一定的顺序排列起来，使用P(n, n) = n!表示n个元素全排列的个数。P(n, n)中的第一个n表示元素的个数，第二个n表示取多少个元素进行排列。

给定一个n个元素数组，其全排列的过程可以描述如下：
（1）任意取一个元素放在第一个位置，则有n种选择；
（2）再剩下的n-1个元素中再取一个元素放在第二个位置则有n-1种选择，此时可以看做对n-1个元素进行全排列；
（3）重复第二步，直到对最后一个元素进行全排列，即最后一个元素放在最后一个位置，全排列结束。

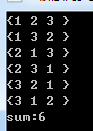
以数组{1,2,3}为例，其全排列的过程如下：
（1）1后面跟（2,3）的全排列；
（2）2后面跟（1,3）的全排列；
（3）3后面跟（1,2）的全排列。

图示如下：

2.2递归实现的优缺点

由于递归将问题逐级分解，因此相对比较容易理解，但是需要消耗大量的栈空间，如果函数栈空间不够，那么就运行不下去了，而且函数调用开销也比较大。

2.3具体实现

#include 
using namespace std;

int sum=0; //全排列个数

//打印数组内容
void print(int array[],int len){
    printf("{");
    for(int i=0; icout<<array[i]<<" ";
    printf("}\n");
}

//实现两数交换
void swap(int* o,int i,int j){
    int tmp = o[i];
    o[i] = o[j];
    o[j] = tmp;
}

//递归实现数组全排列并打印
void permutation(int array[],int len,int index){
    if(index==len){//全排列结束
        ++sum;
        print(array,len);
    }
    else
        for(int i=index;i//将第i个元素交换至当前index下标处
            swap(array,index,i);

            //以递归的方式对剩下元素进行全排列
            permutation(array,len,index+1);

            //将第i个元素交换回原处
            swap(array,index,i);
        }
}

int main(){
    int array[3]={1,2,3};
    permutation(array,3,0);
    cout<<"sum:"<

注意事项：循环将数组中所有元素与第一个元素交换时，再对子数组进行全排列后，需要将第一个元素交换回来，以供下一个元素与第一个元素交换。

运行结果如下：

2.4考虑数组元素中有重复的元素

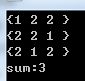
还是以数组{1,2,3}为例，如果数组中有重复的元素，变成了{1,2,2}，那么它的全排列就不能完全按照上面的方法求解，需要做稍微的改动。

因为全排列是将不同元素依次换到当前位置后，再对后面的元素求全排列。如果将重复的元素多次换到当前位置的话，那么就会出现相同的排列。为了避免，我们禁止将相同的元素多次换到当前位置即可。

例如，对{1，2，2}，第一个数1与第二个数2交换得到212，然后考虑第一个数1与第三个数2交换，此时由于第三个数等于第二个数，所以第一个数不再与第三个数交换。再考虑212，它的第二个数与第三个数交换可以得到解决221。此时全排列生成完毕。

这样我们也得到了在全排列中去掉重复的规则——去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。

修改后的代码如下：

//是否交换
bool isSwap(int array[],int len,int index){
        for(int i=index+1;iif(array[index]==array[i])
                return false;
        return true;
}

//递归实现有重复元素的数组全排列
void permutation(int array[],int len,int index){
    if(index==len){//全排列结束
        ++sum;
        print(array,len);
    }
    else
        for(int i=index;iif(isSwap(array,len,i)){ //新增判断是否交换
                //将第i个元素交换至当前index下标处
                swap(array,index,i);

                //以递归的方式对剩下元素进行全排列
                permutation(array,len,index+1);

                //将第i个元素交换回原处
                swap(array,index,i);
            }
        }
}

实验结果：

---

3.全排列的非递归实现

3.1排列的字典序简介

全排列的非递归实现需要用到元素排列后的字典序。所谓的字典序就是按照元素的大小对形成排列进行排序。比如{1,2,3}和{1,3,2}，因为前一个排列的第二元素2是小于后一个排列的第二元素3，所以前一个排列排在前面，后一个排列排在后面。

3.2字典序生成全排列的思想

利用字典序来生成全排列的算法思想是：将集合A中的元素的排列，与某种顺序建立一一映射的关系，按照这种顺序，将集合的所有排列全部输出。这种顺序需要保证，既可以输出全部的排列，又不能重复输出某种排列。字典序就是用此种思想输出全排列的一种方式。

3.3字典序生成全排列的基本过程

给定数组A[N]，那么使用字典序输出全排列的方法基本过程描述如下：
（1）将A按元素大小递增排序，形成字典序最小的排列；
（2）左起从A[0]开始寻找最后一个元素A[k]，满足 A[k]<A[k+1](k<n−1) ，n为元素个数;
（3）从A[k+1]向右开始寻找最小的一个A[i]，使得A[i]>A[k];
（4）交换A[k]与A[i]；
（5）对于a[k+1，n-1]，反转该区间内元素的顺序，即a[k+1]与a[n]交换，a[k+2]与a[n-1]交换，……，这样就得到了a[1…n]在字典序中的下一个排列。
（6）重复步骤（2）至（5），直到A按元素大小递减排序，即第二步找不到满足条件的A[k]。

总的来说字典序生成全排列的就是：先排序，再由后向前找第一个替换点，然后由向后向前找第一个比替换点所在元素大的数与替换点交换，最后颠倒替换点后的所有数据。

这里之所以都是从后向前寻找，因为可以提交效率。替换点后面的元素一定是递减排列的，所以只需要从后向前找第一个大于替换点所在的元素就行了。最后颠倒替换点后的所有数据也是让替换点后的数据排列成字典序最小的状态。

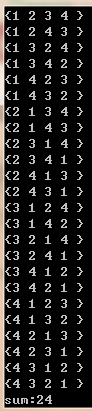
以数组A[3]={1,3,2}为例，字典序输出全排列的具体实现过程如下：
（1）按字典序递增将A排好序，A={1,2,3}，这是字典序最小的第一个排列；
（2）从最后A[2]开始向前寻找第一个元素A[k]，使得A[k]

3.4字典序生成全排列的优缺点

优点：
（1）使用迭代的方式，避免了递归实现的函数栈空间的大量消耗和函数调用的时间开销；
（2）无需考虑数组中出现的重复元素。

缺点：
（1）对数组的排序，增加了时间开销。其实这个可以优化，后面再说；
（2）每次寻找下一个排列时都要对替换点后的元素进行反转，这也增加了时间开销。

3.5字典序生成全排列的具体实现

#include 
using namespace std;

int sum=0;

//打印数组内容
void print(int array[],int len){
    printf("{");
    for(int i=0; icout<<array[i]<<" ";
    printf("}\n");
}

//实现两数交换
void swap(int* o,int i,int j){
    int tmp = o[i];
    o[i] = o[j];
    o[j] = tmp;
}

//实现数组颠倒
void reverse(int array[],int s,int e){
    while(sarray,s,e);
        ++s,--e;
    }
}

//快排比较函数
int compare(const void* a,const void* b){
    return *(int*)(a)-*(int*)(b);//如果小于0，a排在前面b前面
}

//字典序实现数组全排列并打印
void permutation(int array[],int len){
    qsort(array,len,sizeof(array[0]),compare);//快速排序
    ++sum;
    print(array,len);

    while(true){
        int pos=-1;
        //从后往前寻找第一个替换点
        for(int i=len-2;i>=0;--i)
            if(array[i]<array[i+1]){
                pos=i;
                break;
            }
        if(pos==-1)
            return;//排列结束

        //从后向前寻找第一个大于替换点所在元素
        int subsIndex=-1;
        for(int i=len-1;i>pos;--i)
            if(array[i]>array[pos]){
                subsIndex=i;
                break;
            }
        //交换
        swap(array,pos,subsIndex);
        //颠倒
        reverse(array,pos+1,len-1);
        ++sum;
        print(array,len);
    }
}

int main(){
    int A[]={1,4,3,2};
    permutation(A,4);
    cout<<"sum:"<

实验结果截图：

对于有重复元素的数组进行全排列，同样有效。

使用字典序输出集合的全排列需要注意，因为字典序涉及两个排列之间的比较，对于元素集合不方便比较的情况，可以将它们在数组中的索引作为元素，按照字典序生成索引的全排列，然后按照索引输出对应集合元素的排列。这也就省去了
对数组进行排序的操作。

---

参考文献

[1]http://blog.csdn.net/hackbuteer1/article/details/7462447
[2]http://blog.csdn.net/wangshengfeng1986211/article/details/38366709
[3]http://blog.csdn.net/joylnwang/article/details/7064115