【数据结构与算法基础】二叉搜索树和平衡二叉树
写在前面
今天学习在排序和查找中都很有用的特殊二叉树,平衡二叉树和搜索二叉树。
相关代码实现已上传至Github:data_structure/Tree/
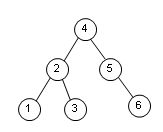
1.二叉搜索树(Binary Search Tree)
二叉搜索时是一种对排序和查找都很有用的特殊二叉树。其或者是一棵空树;或者是具有以下性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值
- 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值
- 左、右子树也分别为二叉排序树
树中结点类实现:
class Node:
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None2.二叉搜索树操作
2.1二叉搜索树的动态查找
当二叉查找树不为空时:
(1)首先将给定值与根结点的关键字比较,若相等,则查找成功
(2)若小于根结点的关键字值,递归查左子树
(3)若大于根结点的关键字值,递归查右子树
(4)若子树为空,查找不成功
如下列出了二叉搜索树查找的递归算法
def search(self, node, parent, data):
if node is None:
return False, node, parent
if node.data == data:
return True, node, parent
if node.data > data:
return self.search(node.lchild, node, data)
else:
return self.search(node.rchild, node, data)若要查找树中的最大(最小)元素,分析结构可知:
二叉查找树的最左边的结点即为最小值,要查找最小值。仅仅需遍历左子树的结点直到为空为止。同理,最右边的结点结尾最大值。要查找最大值,仅仅需遍历右子树的结点直到为空为止。
最小元素查找python代码实现如下,最大元素同理:
def findmin(root):
if root.left:
return findmin(root.left)
else:
return root2.2 BST的插入
将元素插入BST中关键是找到元素应该插入的位置。位置的确定可以利用与查找函数search类似的方法,如果在树中找到 说明要插入的元素已经存在,可放弃插入操作。如果没有找到,查找终止的位置就是应该插入的位置。
def insert(self, data):
flag, n, p = self.search(self.root, self.root, data)
if not flag:
new_node = Node(data)
if data > p.data:
p.rchild = new_node
else:
p.lchild = new_node2.3 BST的删除
二叉搜索树的删除比较复杂,要删除结点在树中的位置决定了操作所采取的策略。可分为以下三种情况:
1.要删除的是叶结点。可以直接删除,然后修改其父节点的指针,置空即可。
2.如果要删除的节点只有一个孩子结点,删除之前需要改变其父节点的指针,指向要删除结点的孩子结点。
3.如果要删除的节点有左右两棵子树,究竟用那棵子树的根结点来填充删除结点的位置?
第一种方法是取其右子树中的最小元素;另一种方法是取其左子树的最大元素。
代码实现如下:
def delete(self, root, data):
flag, n, p = self.search(root, root, data)
if flag is False:
print "无该关键字,删除失败"
else:
if n.lchild is None:
if n == p.lchild:
p.lchild = n.rchild
else:
p.rchild = n.rchild
del n
elif n.rchild is None:
if n == p.lchild:
p.lchild = n.lchild
else:
p.rchild = n.lchild
del n
else: # 左右子树均不为空
pre = n.rchild
if pre.lchild is None:
n.data = pre.data
n.rchild = pre.rchild
del pre
else:
next = pre.lchild
while next.lchild is not None:
pre = next
next = next.lchild
n.data = next.data
pre.lchild = next.rchild
del next3.平衡二叉树(AVL树)
平衡二叉搜索树又称AVL树,它能保证二叉树高度相对平衡,尽量降低二叉树的高度,提高搜索效率。单纯的二叉搜索树在最坏的情况下插入查找删除等操作时间复杂度会是O(N),AVL树就能避免这种情况,使得增删查改的时间复杂度为O(lgN).
AVL树的特点:
- 任一结点的左右子树均为AVL树
- 根结点左右子树高度差的绝对值不超过1
- 每个节点都有一个平衡因子(balance factor--bf),任一节点的平衡因子是-1,0,1。(每个节点的平衡因子等于右子树的高度减去左子树的高度 ) .
3.1 AVL树的调整
当向一颗AVL树中插入新的节点时,该节点的平衡因子很可能不在上述集合范围内,破坏树的平衡。这时候就需要做调整。
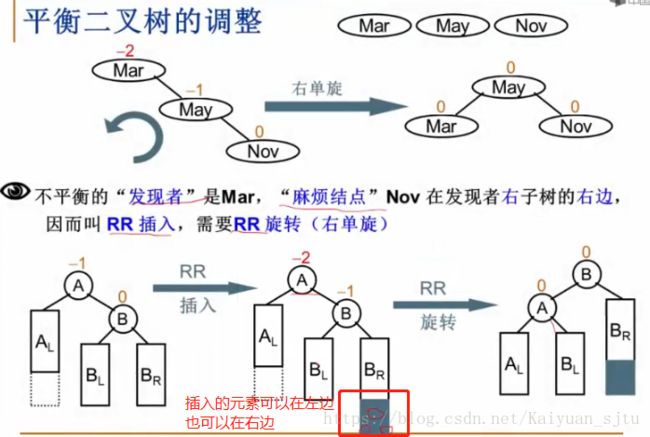
1. 单旋调整
- RR旋转
- LL旋转
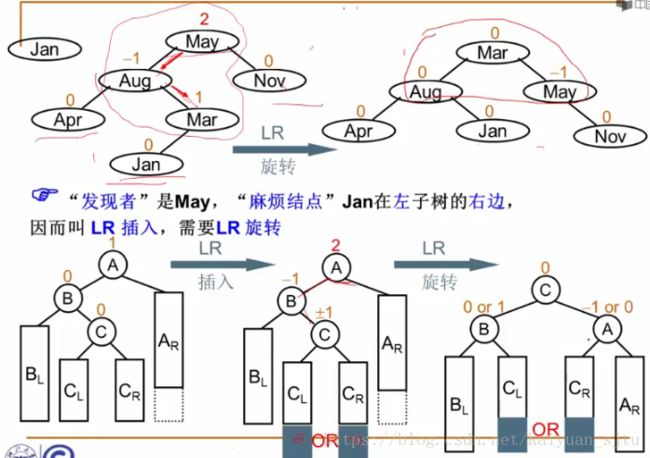
2.双旋调整
- LR旋转
- RL旋转
python代码实现如下:
class ALVTreeNode():
def __init__(self, data, height, freq, left, right):
self.data = data;
self.height = height;
self.freq = freq;
self.left = left;
self.right = right;
#小于<法则
def less(x1, x2):
return x1 < x2;
class ALVTree():
def __init__(self):
self.root = None;
self.left = None;
self.right = None;
def setValue(self, root, left, right):
self.root = root;
self.left = left;
self.right = right;
def getValue(self):
return [self.root, self.left, self.right];
def info(self, node):
if (node == None):
info = 'None';
else:
if (node.left == None):
sL = 'None';
else:
sL = node.left.data;
if (node.right == None):
sR = 'None';
else:
sR = node.right.data;
info = [node.data, node.height, node.freq, sL, sR];
print(info);
def genNode(self, data, height, freq, left, right):
return ALVTreeNode(data, height, freq, left, right);
def height(self, node):
if (node == None):
return 0;
else:
lh = self.height(node.left);
rh = self.height(node.right);
node.height = max(lh, rh)+1;
return node.height;
#左左情况下的旋转
#输入的是高度最高的节点,也就是待处理的root
def rotateLL(self, k2):
k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k2.height = max(self.height(k2.left), self.height(k2.right))+1;
k1.height = max(self.height(k1.left), k2.height)+1;
return k1;
#右右情况下的旋转
#输入的是高度最高的节点,也就是待处理的root
def rotateRR(self, k2):
k1 = k2.right;
k2.right = k1.left;
k1.left = k2;
k2.height = max(self.height(k2.left), self.height(k2.right))+1;
k1.height = max(self.height(k1.right), k2.height)+1;
return k1;
#左右情况的旋转
#输入的是高度最高的节点,也就是待处理的root
def rotateLR(self, k3):
k1 = self.rotateRR(k3.left);
k3.left = k1;
k2 = self.rotateLL(k3);
return k2;
#右左情况的旋转
#输入的是高度最高的节点,也就是待处理的root
def rotateRL(self, k3):
k1 = self.rotateLL(k3.right);
k3.right = k1;
k2 = self.rotateRR(k3);
return k2;
#平衡值
def balanceFlag(self, node):
return self.height(node.left)-self.height(node.right);
#左平衡
def LBalance(self, root):
p = root;
c = p.left;
rc = c.right;
cbf = self.balanceFlag(c);
if (cbf == 1):
root = self.rotateLL(root);
elif (cbf == -1):
root = self.rotateLR(root);
return root;
#右平衡
def RBalance(self, root):
p = root;
c = p.right;
lc = c.left;
cbf = self.balanceFlag(c);
if (cbf == -1):
root = self.rotateRR(root);
elif (cbf == 1):
root = self.rotateRL(root);
return root; 以上,欢迎交流指正~
2018.04.28