相机标定(二)——图像坐标与世界坐标转换

因本文存在错误与模糊之处，为此进行重写修改，但因CSDN不支持富文本转换Markdown，所以重写发布新的博文：

https://blog.csdn.net/Kalenee/article/details/99207102

 

一、坐标变换详解

1.1 坐标关系

相机中有四个坐标系，分别为world，camera，image，pixel

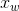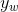• world为世界坐标系，可以任意指定轴和轴，为上图P点所在坐标系。
• camera为相机坐标系，原点位于小孔，z轴与光轴重合，轴和轴平行投影面，为上图坐标系。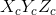
• image为图像坐标系，原点位于光轴和投影面的交点，轴和轴平行投影面，为上图坐标系xy。
• pixel为像素坐标系，从小孔向投影面方向看，投影面的左上角为原点，uv轴和投影面两边重合，该坐标系与图像坐标系处在同一平面，但原点不同。

1.2 坐标转换

下式为像素坐标pixel与世界坐标world的转换公式，左侧第一个矩阵为相机内参数矩阵，第二个矩阵为相机外参数矩阵。假设图像坐标已知，同时相机内参数矩阵通过标定已获取，还需计算比例系数s和外参数矩阵。

• 比例系数s

转换公式可简化为：

M为相机内参数矩阵，R为旋转矩阵，t为平移矩阵，为世界坐标系高度，可设置为0。

通过矩阵变换可得下式：

求解出旋转矩阵和平移矩阵即可算得s。

• 外参数矩阵

Perspective-n-Point是通过n组给定点的世界坐标与像素坐标估计相机位置的方法。OpenCV内部提供的函数为solvePnP()，函数介绍如下：

bool solvePnP(InputArray objectPoints, 
	      	  InputArray imagePoints, 
	      	  InputArray cameraMatrix, 
	      	  InputArray distCoeffs, 
              OutputArray rvec, 
              OutputArray tvec, 
              bool useExtrinsicGuess=false, 
              int flags=ITERATIVE )

• objectPoints，输入世界坐标系中点的坐标；
• imagePoints，输入对应图像坐标系中点的坐标；
• cameraMatrix, 相机内参数矩阵；
• distCoeffs, 畸变系数；
• rvec, 旋转向量，需输入一个非空Mat，需要通过cv::Rodrigues转换为旋转矩阵；
• tvec, 平移向量，需输入一个非空Mat；
• useExtrinsicGuess, 默认为false，如果设置为true则输出输入的旋转矩阵和平移矩阵；
• flags，选择采用的算法；
  • CV_ITERATIVE Iterative method is based on Levenberg-Marquardt optimization. In this case the function finds such a pose that minimizes reprojection error, that is the sum of squared distances between the observed projections imagePoints and the projected (using projectPoints() ) objectPoints .
  • CV_P3P Method is based on the paper of X.S. Gao, X.-R. Hou, J. Tang, H.-F. Chang “Complete Solution Classification for the Perspective-Three-Point Problem”. In this case the function requires exactly four object and image points.
  • CV_EPNP Method has been introduced by F.Moreno-Noguer, V.Lepetit and P.Fua in the paper “EPnP: Efficient Perspective-n-Point Camera Pose Estimation”.

注意：solvePnP的参数rvec和tvec应该都是double类型的

 

二、程序实现

（1）计算参数s和旋转平移矩阵，需要输入一系列的世界坐标系的点及其对应的图像坐标系的点。

//输入参数
Mat cameraMatrix = Mat(3, 3, CV_32FC1, Scalar::all(0)); /* 摄像机内参数矩阵 */
Mat distCoeffs = Mat(1, 5, CV_32FC1, Scalar::all(0)); /* 摄像机的5个畸变系数：k1,k2,p1,p2,k3 */
double zConst = 0;//实际坐标系的距离，若工作平面与相机距离固定可设置为0
	
//计算参数
double s;
Mat rotationMatrix = Mat (3, 3, DataType::type);
Mat tvec = Mat (3, 1, cv::DataType::type);
void calcParameters(vector imagePoints, vector objectPoints)
{
	//计算旋转和平移
	Mat rvec(3, 1, cv::DataType::type);
	cv::solvePnP(objectPoints, imagePoints, cameraMatrix, distCoeffs, rvec, tvec);
	cv::Rodrigues(rvec, rotationMatrix);
}

（2）根据输入的图像坐标计算世界坐标。

Point3f getWorldPoints(Point2f inPoints)
{
    //获取图像坐标
    cv::Mat imagePoint = cv::Mat::ones(3, 1, cv::DataType::type); //u,v,1
	imagePoint.at(0, 0) = inPoints.x;
	imagePoint.at(1, 0) = inPoints.y;

	//计算比例参数S
	cv::Mat tempMat, tempMat2;
	tempMat = rotationMatrix.inv() * cameraMatrix.inv() * imagePoint;
	tempMat2 = rotationMatrix.inv() * tvec;
	s = zConst + tempMat2.at(2, 0);
	s /= tempMat.at(2, 0);

    //计算世界坐标
	Mat wcPoint = rotationMatrix.inv() * (s * cameraMatrix.inv() * imagePoint - tvec);
	Point3f worldPoint(wcPoint.at(0, 0), wcPoint.at(1, 0), wcPoint.at(2, 0));
	return worldPoint;
}

 

参考

http://answers.opencv.org/question/62779/image-coordinate-to-world-coordinate-opencv/

https://stackoverflow.com/questions/12299870/computing-x-y-coordinate-3d-from-image-point

https://docs.opencv.org/2.4/modules/calib3d/doc/camera_calibration_and_3d_reconstruction.html

《视觉SLAM十四讲》——相机与图像