NOIP2014 提高组复赛解题报告

NOIP2014 提高组复赛

---

day1

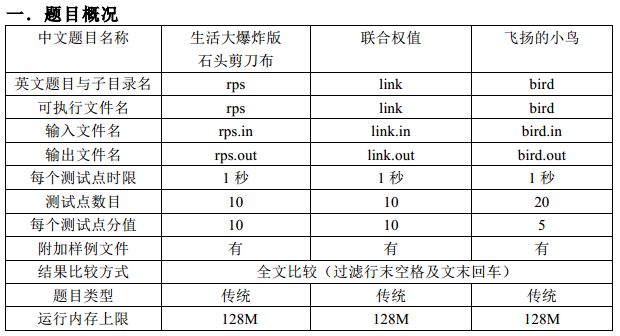
1002. 联合权值

• 树形dp

想用树形dp进行收集的时候，把儿子们的信息给重新收集一遍了，还用了邻接表（甚至本来想用vector）。实际上在收集的时候只要维护权值总和以及最大权值就好了，而不需要再把所有儿子重新提出来再处理。因为这个地方没有优化结果TLE了三组……qvq

但是简直比Tyvj的模拟题还水……好歹人家有五个点……

按照树形dp的思想，我们统计经过当前子树的根的，这棵子树内符合条件的三元点对数目。那么对于这个根，它有两种情况：

• 根是三元点对中的中间结点，此时两端节点是它的儿子中的任意一对。
• 根是三元点对中的两端节点，此时另一端节点是它的孙子。

这样显然是不会重复的，因为我们只考虑当前子树的情况（即不考虑父亲和祖父节点等的情况），并且一定收集包含根结点的三元点对。那么我们只需要统计孙子节点和儿子节点的权值和与最大权值（孙子节点的数据在以儿子节点为根的时候已经收集到了），于是时间复杂度为 O(n) 。

#include 
#include 
#include 
#include 
#include 
#define M 200005
#define P 10007
#define clear(x,val) memset(x,val,sizeof(x))
using namespace std;
template <class temp>
inline void Rd(temp &res){
    res=0;char c;
    while(c=getchar(),c<48);
    do res=(res<<3)+(res<<1)+(c^48);
    while(c=getchar(),c>47);
}
inline void Mod(int &a,int b){a+=b;if(a>=P)a-=P;}
//-----------------------
int n,w[M];
int head[M],htop=0;
struct node{int v,nxt;}Nodes[M<<1];
int mxson[M],sumson[M];
void add_edge(int u,int v){
    Nodes[++htop]=(node){v,head[u]};head[u]=htop;
    Nodes[++htop]=(node){u,head[v]};head[v]=htop;
}
int val,mx=0,ans=0;
void dfs(int u,int pre){
    for(int j=head[u];~j;j=Nodes[j].nxt){
        int v=Nodes[j].v;
        if(v==pre)continue;
        dfs(v,u);
        mx=max(mxson[u]*w[v],mx);
        if(mxson[u]int main(){
    clear(head,-1);
    Rd(n);
    for(int i=1,u,v;ifor(int i=1;i<=n;i++)Rd(w[i]);
    dfs(1,0);
    Mod(ans,ans);
    printf("%d %d\n",mx,ans);
}

如果不从正常的树形dp考虑，那么我们就枚举每个点作为中心节点的情况，此时它周围一圈的相邻节点中均可以构成两端点对。于是每次统计一下，时间复杂度为 O(n) 。

1003. Flappy Bird

• 背包dp

玩Codevs的玩了这么久还A不掉也是可以。又是受了上次NOIP2013_day2_task3华容道那题的影响……居然肛在选择dfs还是bfs好久……然而我一开始还是敲了dfs qvq，真的害怕如果标程又是dfs，然后我居然写了bfs，那时候我会哭的一脸懵逼的。

后来硬是改成了Dijkstra，想想复杂度有点高于是准备改成队列……虽然没改成功，但是我最后意识到——这题是不是可以用背包做。 qvq 但是硬是水了75分，比暴力背包高（难道完全背包的优化不暴力么……）。

bfs还是简单的，只不过由于每次转移的边权在 [0,m] 中，不是恒定的1，所以只能用堆弹。时间复杂度为 O(n×m2logn) 。但是稍微加一点强劲判重就可以到75分。

实际上写了bfs之后，可以发现每次转移只会在相邻两个横坐标之间，而且只有两种转移操作：

• 向上跳跃，此时可跳跃次数为 ∞ ，但是符合题意的跳跃次数在一定范围内， hi=k×upi−1+hi−1 。
• 向下掉落，此时只能掉落 downi−1 的高度。
• 两个步骤在一组转移中只会进行一个。

直接转移的复杂度是 O(n×m2) 。
显然第一个操作类似于完全背包，可以采用完全背包的做法进行优化（背包九讲）；而第二个操作类似01背包。两个做法分开来更新即可避免重复。于是最终复杂度为 O(nm) 。

似乎滚动还会更慢一点……反正空间只有128M不成问题。

#include 
#include 
#include 
#include 
#include 
#define clear(x,val) memset(x,val,sizeof(x))
#define N 10005
#define M 1005
#define inf 0x3f3f3f3f
using namespace std;
template <class temp>
inline void Rd(temp &res){
    res=0;char c;
    while(c=getchar(),c<48);
    do res=(res<<3)+(res<<1)+(c^48);
    while(c=getchar(),c>47);
}

int n,m,k;
int up[N],down[N],L[N],R[N];
bool pipe[N];
int dp[N][M];
inline bool judge(int w,int h){return L[w]<=h&&h<=R[w];}
inline void check(int &a,int b){if(a==-1||a>b)a=b;}
int main(){
    Rd(n),Rd(m),Rd(k);
    for(int i=0;i<=n-1;i++)Rd(up[i]),Rd(down[i]);
    for(int i=0;i<=n;i++)L[i]=1,R[i]=m;
    for(int i=1,pos,l,h;i<=k;i++){
        Rd(pos),Rd(l),Rd(h);
        L[pos]=l+1,R[pos]=h-1;
        pipe[pos]=true;
    }

    clear(dp,-1);
    for(int j=L[0];j<=R[0];j++)dp[0][j]=0;

    for(int i=1;i<=n;i++){
        for(int j=L[i-1];j<=R[i-1];j++)
            if(~dp[i-1][j]){
                int nxth=j+up[i-1];
                if(nxth>R[i]){
                    if(R[i]==m)check(dp[i][m],dp[i-1][j]+1);
                }else check(dp[i][nxth],dp[i-1][j]+1);
            }
        for(int j=1;j//完全背包优化，注意仍要从1开始
            if(~dp[i][j]){
                int nxth=j+up[i-1];
                if(nxth>R[i]){
                    if(R[i]==m)check(dp[i][m],dp[i][j]+1);
                }else check(dp[i][nxth],dp[i][j]+1);
            }
        for(int j=L[i-1];j<=R[i-1];j++)
            if(~dp[i-1][j]&&judge(i,j-down[i-1]))
                check(dp[i][j-down[i-1]],dp[i-1][j]);
    }

    int ans=-1;
    for(int i=L[n];i<=R[n];i++)
        if(~dp[n][i])check(ans,dp[n][i]);

    if(!~ans){
        int cnt=0;
        for(int i=0;i<=n;i++){
            bool flag=false;
            for(int j=1;j<=m;j++)if(~dp[i][j]){flag=true;break;}
            if(flag)cnt+=pipe[i];
            else break;
        }
        printf("0\n%d\n",cnt);  
    }else printf("1\n%d\n",ans);
}

---

day2

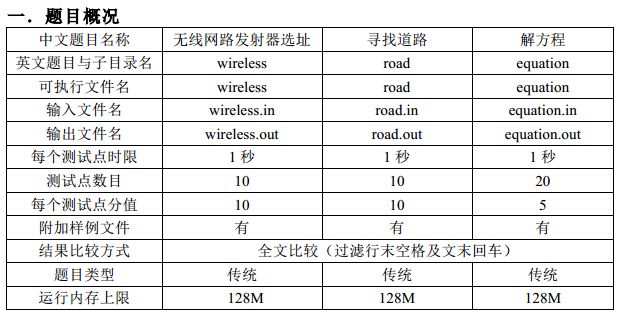
1005. 寻找路径

• 模拟+最短路

这题的题意有点迷。由于要求路径上的点，无论经过哪条出边，都可以到达终点。这些点是可以预处理出来的，但是在预处理的时候我没有将因为终点走反向边到不了的点和所有出边中有一端点无法到达终点的点分开来处理，所以更新就爆炸了qvq。

但是实际上最大的错误在于我·把·正·解·改·错·了！而且自己也没有对拍，结果我在修改变量名和省掉另外一个标记数组的时候没有半点意识。以后依旧是要多对拍，然后除非是修改时间复杂度，否则不要对变量名太过纠结吧。

但是自己修改的原因也是为了理清思路……因为那个表述奇怪的条件还全部写错了一次……不理一理思路我反而更没底。

如上，预处理出那些可以到达的点，于是需要从终点开始跑一边反向边，再筛掉那些出边到不了终点的点。在第二次筛选的过程中一定要注意，第二次筛选出的点不能当做第一次的筛选点。最后再在这些残缺的点上跑bfs即可。

时间复杂度为 O(n) 。

#include 
#include 
#include 
#include 
#include 
#define clear(x,val) memset(x,val,sizeof(x))
#define N 10005
#define M 200005
using namespace std;
template <class temp>
inline void Rd(temp &res){
    res=0;char c;
    while(c=getchar(),c<48);
    do res=(res<<3)+(res<<1)+(c&15);
    while(c=getchar(),c>47);
}
int n,m,st,gt,head[N],rhead[N];
struct edge{int to,nxt;}Edge[M<<1],rEdge[M<<1];
void add_edge(int u,int v,int top){
    Edge[top]=(edge){v,head[u]};head[u]=top;
    rEdge[top]=(edge){u,rhead[v]};rhead[v]=top;
}
bool vis[N];
void rdfs(int u,int pre){
    vis[u]=true;
    for(int j=rhead[u];j;j=rEdge[j].nxt){
        int v=rEdge[j].to;
        if(v!=pre&&!vis[v])rdfs(v,u);
    }
}
int dis[N];
bool mark[N];
void bfs(int st){
    clear(dis,-1);
    queue<int>q;

    if(!mark[st])q.push(st),dis[st]=0;

    while(!q.empty()){
        int u=q.front();q.pop();
        for(int j=head[u];j;j=Edge[j].nxt){
            int v=Edge[j].to;
            if(!~dis[v]&&!mark[v]){
                dis[v]=dis[u]+1;
                q.push(v);
            }
        }
    }
}
int main(){
    Rd(n),Rd(m);
    for(int i=1;i<=m;i++){
        int u,v;Rd(u),Rd(v);
        add_edge(u,v,i);
    }
    Rd(st),Rd(gt);

    rdfs(gt,0);
    for(int i=1;i<=n;i++)
        if(!vis[i])mark[i]=true;
        else for(int j=head[i];j;j=Edge[j].nxt){
            int v=Edge[j].to;
            if(!vis[v]){mark[i]=true;break;}
        }
    bfs(st);
    printf("%d\n",dis[gt]);
}

1006.解方程

• 高精度
• Hash

怎么说呢……第一次成功实现带负数的大高精，结果只能得50分……随便去个模就有70分而且多找几个模底就可以A了这种事情……也是服气。

暴力做法是直接枚举所有的x，然后再计算整个式子是否满足左右式相等。实际上根本不需要支持负数高精的……把负数的大高精移到右侧就可以了 qvq。时间复杂度 O(1002nm) 。

正解做法是大整数取模，然后在低精范围内计算。做法成立基于以下等式：

a+b≡a%P+b%P(modP)

a×b≡a%P×b%P(modP)

于是将每个大整数压成可以在int范围内计算的式子即可。这样复杂度就降下来了，但是正确性就不能保证，显然只要多取几个模底就好了。但是对于 x 我们没有什么好方法求（当然大神肯定可以直接解出来），时间复杂度为 O(nm) ，时间复杂度还是不能保证。

我们可以把模底再压的小一些，那么 equation(x)≡equation(x%P)(modP) ，所以我们可以先把每个模底所有可能的情况都处理出来，那么枚举的时候就可以 O(1) 判断了。时间复杂度为 O(m+nP) 。

#include 
#include 
#include 
#include 
using namespace std;
int prime[10]={9887,9901,9907,9923,9929,9931,9941,9949,9967,9973};
int f[10][10000];
int p[10][105];
char str[10005];
struct Bigint{
    #define M 3005
    #define P 10000
    int num[M],len,fu;
    Bigint(){
        memset(num,0,sizeof(num));
        len=1,fu=0;
    }
    void read(){
        scanf("%s",str);
        if(str[0]=='-')fu=1;
        len=0;
        for(int sz=strlen(str),i=sz-1;i>=fu;i-=4){
            num[len]=0;
            for(int j=max(i-3,fu);j<=i;j++)
                num[len]=num[len]*10+(str[j]&15);
            ++len;
        }
        if(len==1&&!num[len-1])fu=0;
    }
    int operator % (const int &a)const{
        Bigint b;b=*this;
        for(int i=b.len-1;i>=0;i--){
            b.num[i]%=a;
            if(i)b.num[i-1]+=b.num[i]*P;
        }
        if(fu)b.num[0]*=-1;
        b.num[0]=(b.num[0]%a+a)%a;
        return b.num[0];
    }
}a[105];
vector<int>ans;
bool check(int a){
    for(int t=0;t<10;t++){
        int b=a%prime[t];
        if(f[t][b])return false;
    }
    return true;
}
int main(){
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=0;i<=n;i++)
        a[i].read();
    for(int t=0;t<10;t++){
        for(int i=0;i<=n;i++)
            p[t][i]=a[i]%prime[t];
        for(int x=0;xfor(int i=n;i>=0;i--)
                f[t][x]=(f[t][x]*x+p[t][i])%prime[t];
    }
    for(int i=1;i<=m;i++)
        if(check(i))ans.push_back(i);
    printf("%d\n",ans.size());
    for(int i=0;iprintf("%d\n",ans[i]);
}