机器学习与R语言实战-第二章（MachineLearningWithRCookbook_chapter2）

#
# machine Learning with R cook book chapter 2
#
   # the Titanic data can be obtained from titanic package 
   # or this link https://www.kaggle.com/c/titanic/data
   #
install.packages("titanic")
library(titanic)
train.data <- data(titanic_train)
write.csv(titanic_train,"D:/mlwrcbdataset/titanic_train.csv",row.names = TRUE)  
#  load Titnic data set
train.data = read.csv(file="D:/mlwrcbdataset/titanic_train.csv", header = TRUE, sep = ",",na.strings = c("NA","")) 
# check the loaded data with the str function:
str(train.data)

'data.frame': 891 obs. of  13 variables:
 $ X          : int  1 2 3 4 5 6 7 8 9 10 ...
 $ PassengerId: int  1 2 3 4 5 6 7 8 9 10 ...
 $ Survived   : int  0 1 1 1 0 0 0 0 1 1 ...
 $ Pclass     : int  3 1 3 1 3 3 1 3 3 2 ...
 $ Name       : Factor w/ 891 levels "Abbing, Mr. Anthony",..: 109 191 358 277 16 559 520 629 417 581 ...
 $ Sex        : Factor w/ 2 levels "female","male": 2 1 1 1 2 2 2 2 1 1 ...
 $ Age        : num  22 38 26 35 35 NA 54 2 27 14 ...
 $ SibSp      : int  1 1 0 1 0 0 0 3 0 1 ...
 $ Parch      : int  0 0 0 0 0 0 0 1 2 0 ...
 $ Ticket     : Factor w/ 681 levels "110152","110413",..: 524 597 670 50 473 276 86 396 345 133 ...
 $ Fare       : num  7.25 71.28 7.92 53.1 8.05 ...
 $ Cabin      : Factor w/ 147 levels "A10","A14","A16",..: NA 82 NA 56 NA NA 130 NA NA NA ...

 $ Embarked   : Factor w/ 3 levels "C","Q","S": 3 1 3 3 3 2 3 3 3 1 ...

# transform the variable from the int numeric type to the factor categorical type
#  Survived (0 = No; 1 = Yes) and 
#  Pclass (1 = 1st; 2 = 2nd; 3 = 3rd) are categorical variables
train.data$Survived = factor(train.data$Survived) 
train.data$Pclass   = factor(train.data$Pclass)
str(train.data)

'data.frame': 891 obs. of  13 variables:
 $ X          : int  1 2 3 4 5 6 7 8 9 10 ...
 $ PassengerId: int  1 2 3 4 5 6 7 8 9 10 ...
 $ Survived   : Factor w/ 2 levels "0","1": 1 2 2 2 1 1 1 1 2 2 ...
 $ Pclass     : Factor w/ 3 levels "1","2","3": 3 1 3 1 3 3 1 3 3 2 ...
 $ Name       : Factor w/ 891 levels "Abbing, Mr. Anthony",..: 109 191 358 277 16 559 520 629 417 581 ...
 $ Sex        : Factor w/ 2 levels "female","male": 2 1 1 1 2 2 2 2 1 1 ...
 $ Age        : num  22 38 26 35 35 NA 54 2 27 14 ...
 $ SibSp      : int  1 1 0 1 0 0 0 3 0 1 ...
 $ Parch      : int  0 0 0 0 0 0 0 1 2 0 ...
 $ Ticket     : Factor w/ 681 levels "110152","110413",..: 524 597 670 50 473 276 86 396 345 133 ...
 $ Fare       : num  7.25 71.28 7.92 53.1 8.05 ...
 $ Cabin      : Factor w/ 147 levels "A10","A14","A16",..: NA 82 NA 56 NA NA 130 NA NA NA ...
 $ Embarked   : Factor w/ 3 levels "C","Q","S": 3 1 3 3 3 2 3 3 3 1 ...

# transform the variable from the int numeric type to the factor categorical type
#  Survived (0 = No; 1 = Yes) and 
#  Pclass (1 = 1st; 2 = 2nd; 3 = 3rd) are categorical variables
train.data$Survived = factor(train.data$Survived) 
train.data$Pclass   = factor(train.data$Pclass)
str(train.data)
# Detecting missing values
is.na(train.data$Age)

# how many missing values there are
sum(is.na(train.data$Age) == TRUE)

[1] 177

# the percentage of missing values
sum(is.na(train.data$Age) == TRUE) / length(train.data$Age)

[1] 0.1986532

# a percentage of the missing value of the attributes
sapply(train.data,function(df) {
  sum(is.na(df)==TRUE)/length(df)
})

    X PassengerId    Survived      Pclass        Name         Sex         Age       SibSp       Parch      Ticket 
0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.000000000 0.198653199 0.000000000 0.000000000 0.000000000 
       Fare       Cabin    Embarked 
0.000000000 0.771043771 0.002244669 

   # use the missmap function to plot the missing value map:
install.packages("Amelia")
require(Amelia)
missmap(train.data,main="Missing Map")
# we can also use the interactive GUI of Amelia and AmeliaView,
# To start running AmeliaView, simply type AmeliaView() in the R Console

#
 # Imputing missing values
#
   # First, list the distribution of Port of Embarkation
table(train.data$Embarked, useNA = "always")

C    Q    S  
 168   77  644    2 

   # Assign the two missing values to a more probable port 
   # (that is, the most counted port), which is Southampton in this case:
train.data$Embarked[which(is.na(train.data$Embarked))] = 'S'
table(train.data$Embarked, useNA = "always")

  C    Q    S  
 168   77  646    0 

   # In order to discover the types of titles contained in the names of train.data, we
   # first tokenize train.data$Name by blank (a regular expression pattern as "\\s+"),
   # and then count the frequency of occurrence with the table function. After this, since
   # the name title often ends with a period, we use the regular expression to grep the 
   # word containing the period. In the end, sort the table in decreasing order:
train.data$Name = as.character(train.data$Name)
table_words = table(unlist(strsplit(train.data$Name, "\\s+")))
sort(table_words [grep('\\.',names(table_words))], decreasing=TRUE)

 Mr.     Miss.      Mrs.   Master.       Dr.      Rev.      Col.    Major.     Mlle.     Capt. Countess.      Don. 
      517       182       125        40         7         6         2         2         2         1         1         1 
Jonkheer.        L.     Lady.      Mme.       Ms.      Sir. 
        1         1         1         1         1         1 

  # To obtain which title contains missing values, you can use str_match provided by
   # the stringr package to get a substring containing a period, then bind the column
   # together with cbind. Finally, by using the table function to acquire the statistics of
   # missing values, you can work on counting each title:
library(stringr)
tb = cbind(train.data$Age, str_match(train.data$Name, "[a-zA-Z]+\\."))
table(tb[is.na(tb[,1]),2])

  Dr. Master.   Miss.     Mr.    Mrs. 
      1       4      36     119      17

  # For a title containing a missing value, one way to impute data is to assign the mean
   # value for each title (not containing a missing value):
mean.mr   =  mean(train.data$Age[grepl(" Mr\\.",  train.data$Name) & !is.na(train.data$Age)])
mean.mrs  =  mean(train.data$Age[grepl(" Mrs\\.", train.data$Name) & !is.na(train.data$Age)])
mean.dr   =  mean(train.data$Age[grepl(" Dr\\.",  train.data$Name) & !is.na(train.data$Age)])
mean.miss =  mean(train.data$Age[grepl(" Miss\\.", train.data$Name) & !is.na(train.data$Age)])
mean.master = mean(train.data$Age[grepl(" Master\\.", train.data$Name) & !is.na(train.data$Age)])
   # Then, assign the missing value with the mean value of each title:
train.data$Age[grepl(" Mr\\.", train.data$Name) & is.na(train.data$Age)] = mean.mr
train.data$Age[grepl(" Mrs\\.", train.data$Name) & is.na(train.data$Age)] = mean.mrs
train.data$Age[grepl(" Dr\\.", train.data$Name) & is.na(train.data$Age)] = mean.dr
train.data$Age[grepl(" Miss\\.", train.data$Name) & is.na(train.data$Age)] = mean.miss
train.data$Age[grepl(" Master\\.", train.data$Name) & is.na(train.data$Age)] = mean.master
# Here we list the honorific entry from Wikipedia for your reference. According to it
# (http://en.wikipedia.org/wiki/English_honorific):
#

#
  #  Exploring and visualizing data
#

    # First, you can use a bar plot and histogram to generate descriptive statistics for each
    # attribute, starting with passenger survival:
barplot(table(train.data$Survived), main="Passenger Survival", names= c("Perished", "Survived"))

  # We can generate the bar plot of passenger class:
barplot(table(train.data$Pclass), main="Passenger Class",
        names= c("first", "second", "third"))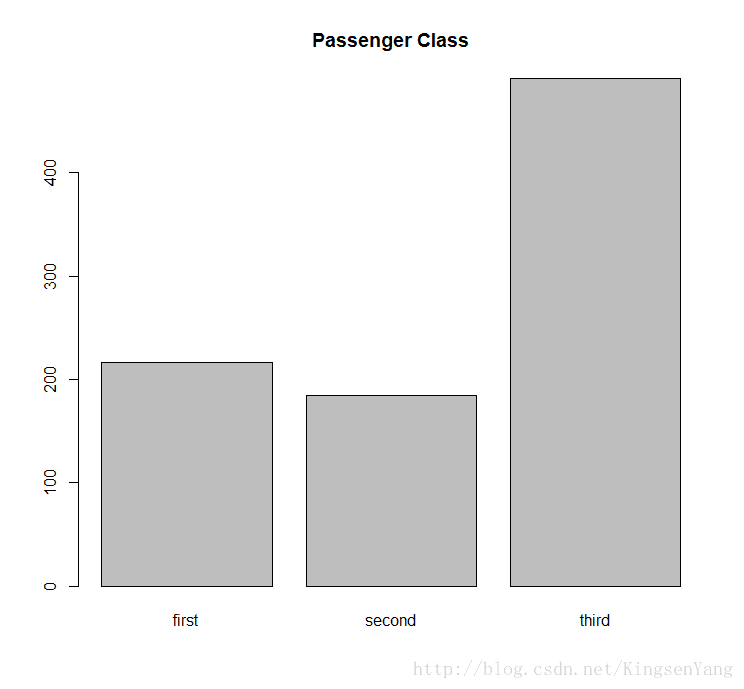

 # Next, we outline the gender data with the bar plot:
barplot(table(train.data$Sex), main="Passenger Gender")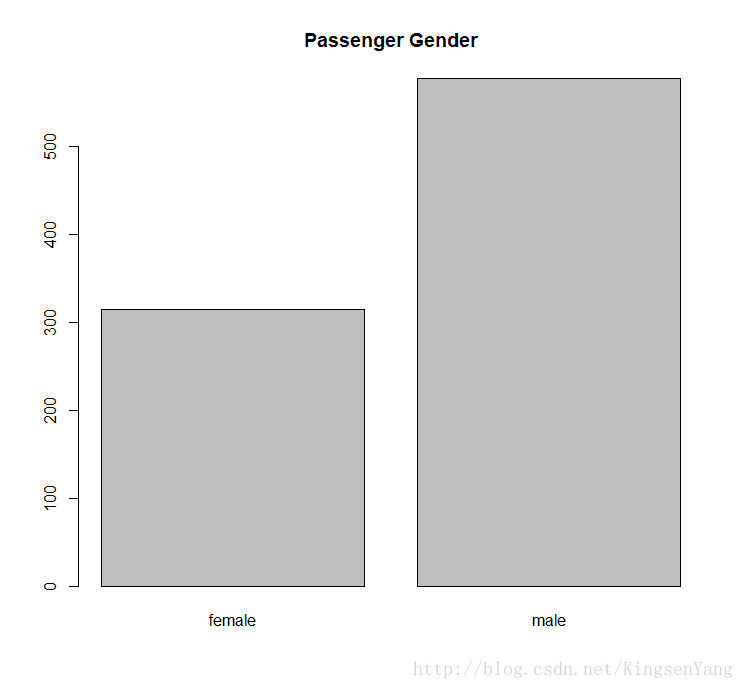

# We then plot the histogram of the different ages with the hist function:
hist(train.data$Age, main="Passenger Age", xlab = "Age")

    # We can plot the bar plot of sibling passengers to get the following:
barplot(table(train.data$SibSp), main="Passenger Siblings")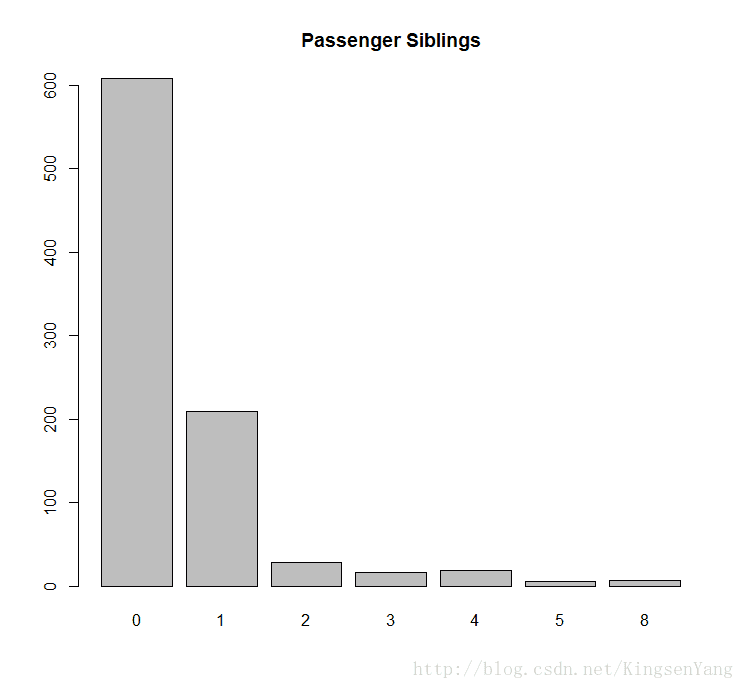

    # Next, we can get the distribution of the passenger parch:
barplot(table(train.data$Parch), main="Passenger Parch")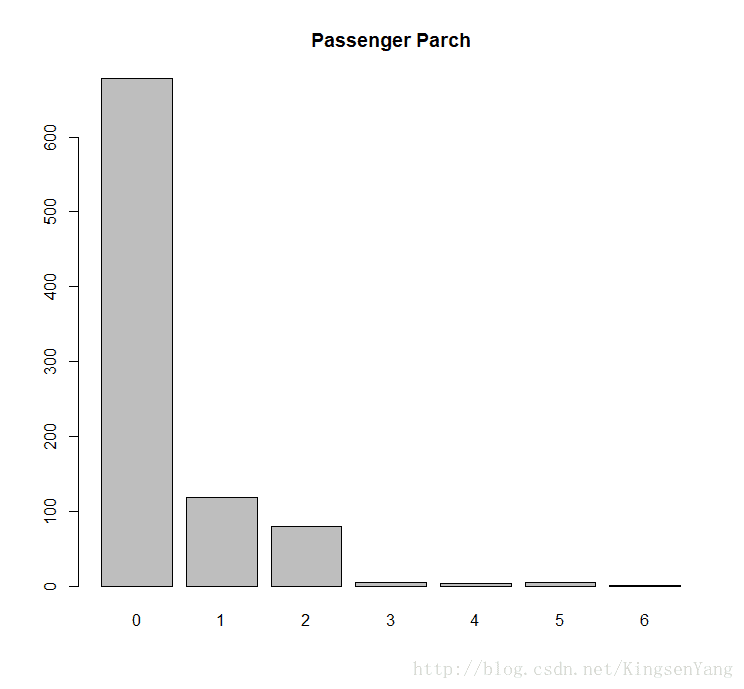

    # Next, we plot the histogram of the passenger fares:
hist(train.data$Fare, main="Passenger Fare", xlab = "Fare")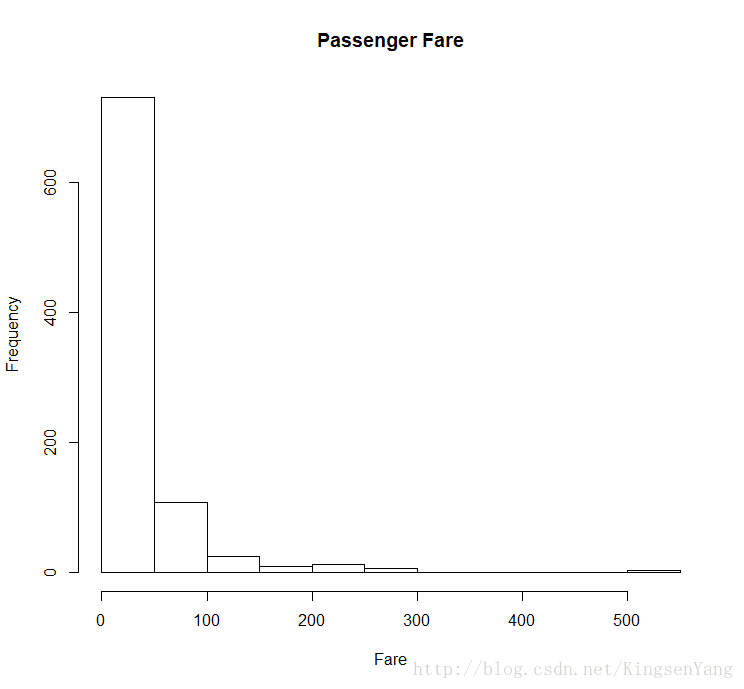

    # Finally, one can look at the port of embarkation:
barplot(table(train.data$Embarked), main="Port of Embarkation")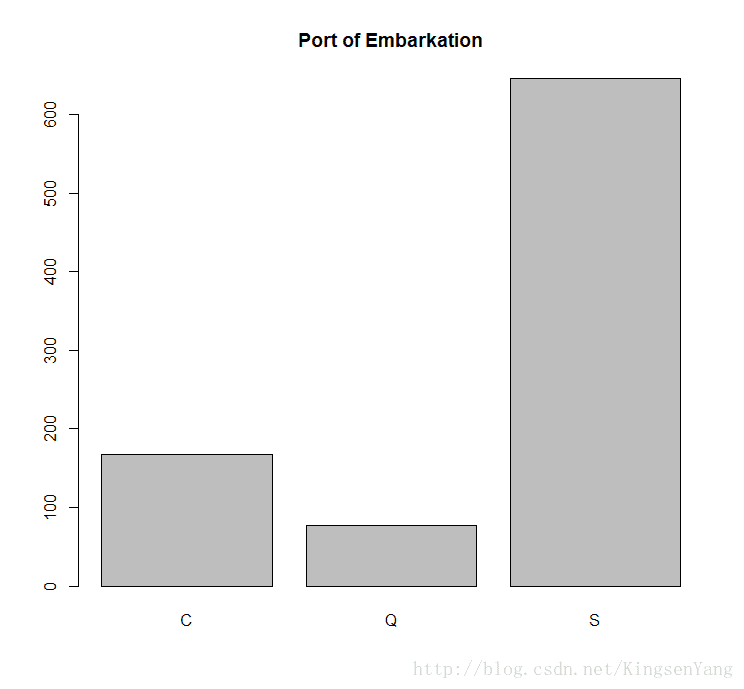

    # Use barplot to find out which gender is more likely to perish during shipwrecks
counts = table( train.data$Survived, train.data$Sex)
barplot(counts, col=c("darkblue","red"), 
        legend = c("Perished", "Survived"),
        main = "Passenger Survival by Sex")

    # Next, we should examine whether the Pclass factor of each passenger 
    # may affect the survival rate: 
counts = table( train.data$Survived, train.data$Pclass)
barplot(counts, col=c("darkblue","red"), 
        legend =c("Perished","Survived"),
        main= "Titanic Class Bar Plot" )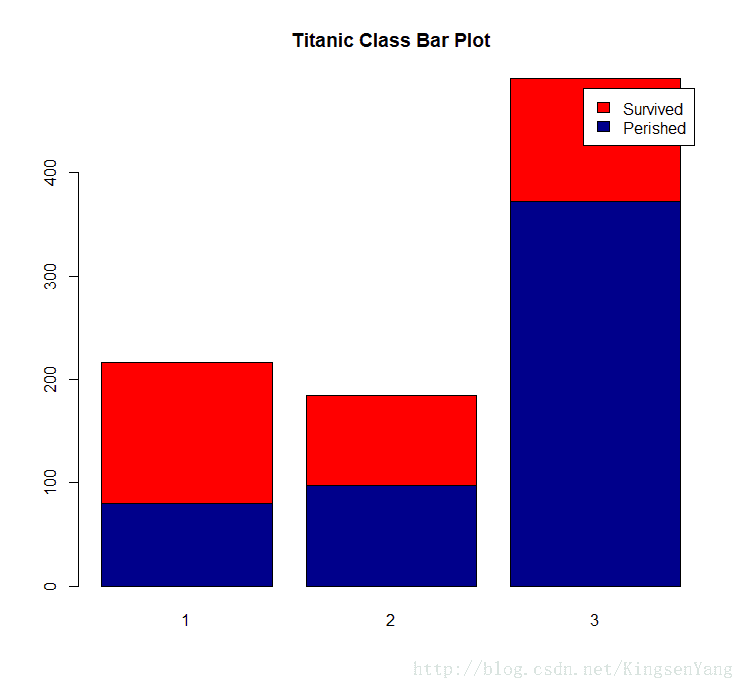

    # Next, we examine the gender composition of each Pclass:
counts = table( train.data$Sex, train.data$Pclass)
barplot(counts, col=c("darkblue","red"), 
        legend = rownames(counts), 
        main= "Passenger Gender by Class")

   # Furthermore, we examine the histogram of passenger ages
hist(train.data$Age[which(train.data$Survived == "0")],
     main= "Passenger Age Histogram", 
     xlab="Age", ylab="Count", col ="blue",
     breaks=seq(0,80,by=2))
hist(train.data$Age[which(train.data$Survived == "1")],
     col  ="red", add = T, 
     breaks=seq(0,80,by=2))

   # To examine more details about the relationship 
   # between the age and survival rate, one can use a boxplot:
boxplot(train.data$Age ~ train.data$Survived,
        main="Passenger Survival by Age",
        xlab="Survived", ylab="Age")

   # To categorize people with different ages into different groups, such as children (below
   # 13), youths (13 to 19), adults (20 to 65), and senior citizens (above 65), 
   # execute the following commands:

train.child = train.data$Survived[train.data$Age < 13]
length(train.child[which(train.child == 1)] ) / length(train.child)

[1] 0.5753425

train.youth = train.data$Survived[train.data$Age >= 15 & train.data$Age < 25]
length(train.youth[which(train.youth == 1)] ) / length(train.youth)

[1] 0.4025424

train.adult = train.data$Survived[train.data$Age >= 20 & train.data$Age < 65]
length(train.adult[which(train.adult == 1)] ) / length(train.adult)

[1] 0.3651685

train.senior = train.data$Survived[train.data$Age >= 65]
length(train.senior[which(train.senior == 1)] ) / length(train.senior)

[1] 0.09090909

  # Apart from using bar plots, histograms, and boxplots to visualize data, one can also apply
    # mosaicplot in the vcd package to examine the relationship between multiple categorical
    # variables. For example, when we examine the relationship between the Survived and
    # Pclass variables, the application is performed as follows:
mosaicplot(train.data$Pclass ~ train.data$Survived,
            main="Passenger Survival Class", color=TRUE,
            xlab="Pclass", ylab="Survived")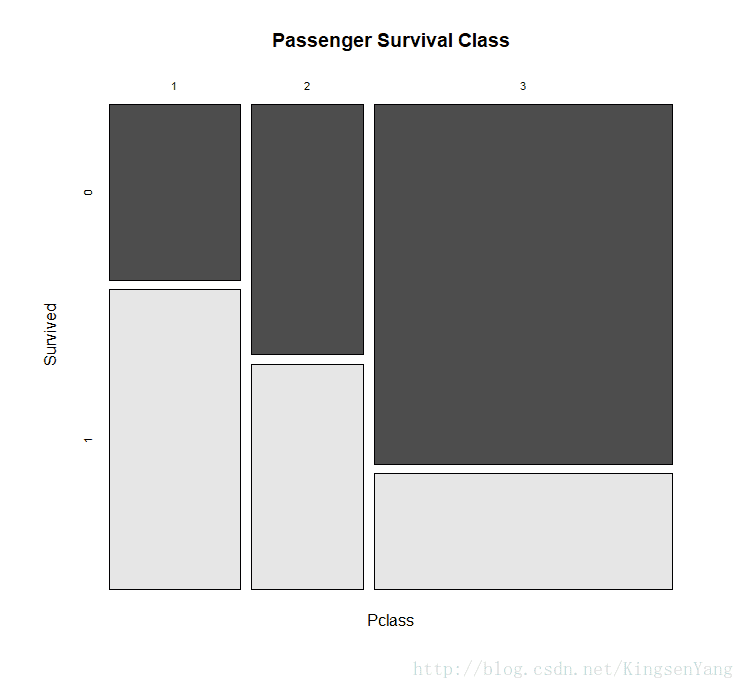

#
#  Predicting passenger survival with a decision tree
#

   # First, we construct a data split split.data function
split.data = function(data, p = 0.7, s = 666){
   set.seed(s)
   index = sample(1:dim(data)[1])
   train = data[index[1:floor(dim(data)[1] * p)], ]
   test = data[index[((ceiling(dim(data)[1] * p)) + 1):dim(data)[1]], ]
   return(list(train = train, test = test))
   }
    # Then, we split the data, with 70 percent assigned to the training dataset and the
    # remaining 30 percent for the testing dataset:
allset= split.data(train.data, p = 0.7)
trainset = allset$train
testset = allset$test
    # For the condition tree, one has to use the ctree function from the party package;
    # therefore, we install and load the party package:
install.packages('party')
require('party')
    # We then use Survived as a label to generate the prediction model in use. After that,
    # we assign the classification tree model into the train.ctree variable:
train.ctree = ctree(Survived ~ Pclass + Sex + Age + SibSp + Fare
                     +Parch + Embarked, data=trainset)
 train.ctree

Conditional inference tree with 7 terminal nodes


Response:  Survived 
Inputs:  Pclass, Sex, Age, SibSp, Fare, Parch, Embarked 
Number of observations:  623 


1) Sex == {male}; criterion = 1, statistic = 173.672
  2) Pclass == {2, 3}; criterion = 1, statistic = 30.951
    3) Age <= 9; criterion = 0.993, statistic = 10.923
      4) SibSp <= 1; criterion = 0.999, statistic = 14.856
        5)*  weights = 10 
      4) SibSp > 1
        6)*  weights = 13 
    3) Age > 9
      7)*  weights = 280 
  2) Pclass == {1}
    8)*  weights = 87 
1) Sex == {female}
  9) Pclass == {1, 2}; criterion = 1, statistic = 59.504
    10)*  weights = 125 
  9) Pclass == {3}
    11) Fare <= 23.25; criterion = 0.997, statistic = 12.456
      12)*  weights = 85 
    11) Fare > 23.25
      13)*  weights = 23 

    # We use a plot function to plot the tree:
 plot(train.ctree, main="Conditional inference tree of Titanic Dataset")
    # There is a similar decision tree based package, named rpart. The difference between party
    # and rpart is that ctree in the party package avoids the following variable selection bias of
    # rpart and ctree in the party package, tending to select variables that have many possible
    # splits or many missing values. Unlike the others, ctree uses a significance testing procedure
    # in order to select variables, instead of selecting the variable that maximizes an information
    # measure.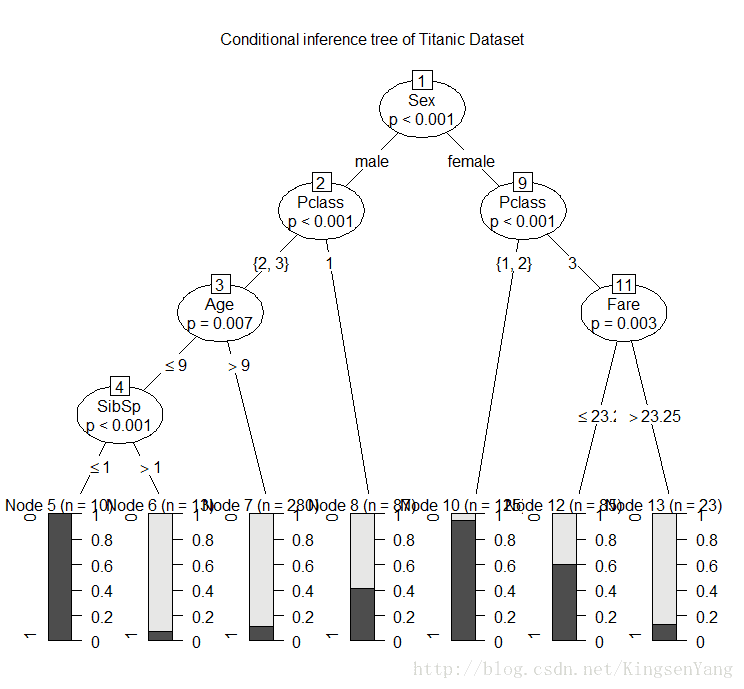

#
# Validating the power of prediction with a confusion matrix 
#

 

    # We start using the constructed train.ctree model to predict the survival of the
    # testing set:
ctree.predict = predict(train.ctree, testset) 
    # First, we install the caret package, and then load it:
install.packages("caret")
require(caret)
    # After loading caret, one can use a confusion matrix to generate the statistics of the
    # output matrix:
confusionMatrix(ctree.predict, testset$Survived)

Confusion Matrix and Statistics


          Reference
Prediction   0   1
         0 160  23
         1  16  68
                                         
               Accuracy : 0.8539         
                 95% CI : (0.8058, 0.894)
    No Information Rate : 0.6592         
    P-Value [Acc > NIR] : 5.347e-13      
                                         
                  Kappa : 0.6688         
 Mcnemar's Test P-Value : 0.3367         
                                         
            Sensitivity : 0.9091         
            Specificity : 0.7473         
         Pos Pred Value : 0.8743         
         Neg Pred Value : 0.8095         
             Prevalence : 0.6592         
         Detection Rate : 0.5993         
   Detection Prevalence : 0.6854         
      Balanced Accuracy : 0.8282         
                                         
       'Positive' Class : 0  

 # Assessing performance with the ROC curve
    # Prepare the probability matrix:
train.ctree.pred = predict(train.ctree, testset)
train.ctree.prob = 1- unlist(treeresponse(train.ctree,testset), use.names=F)[seq(1,nrow(testset)*2,2)]
    # Install and load the ROCR package:
install.packages("ROCR")
require(ROCR)
    # Create an ROCR prediction object from probabilities
train.ctree.prob.rocr = prediction(train.ctree.prob,testset$Survived)
    # Prepare the ROCR performance object for the ROC curve (tpr=true positive
    # rate, fpr=false positive rate) and the area under curve (AUC):
train.ctree.perf = performance(train.ctree.prob.rocr,"tpr","fpr")
train.ctree.auc.perf = performance(train.ctree.prob.rocr,
                                   measure = "auc", x.measure = "cutoff") 
    # Plot the ROC curve, with colorize as TRUE, and put AUC as the title:
plot(train.ctree.perf, col=2,colorize=T,
     main=paste("AUC:", [email protected]))