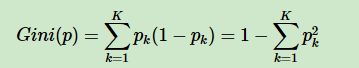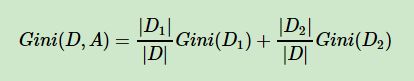决策树CART算法原理详解

大家好，今天用一个简单的例子来给大家介绍一下决策树中的CART算法。

CART分类树

CART分类树适用于预测结果为离散型数据的情况下，主要是计算每一组特征的Gini系数增益来确定决策树划分的优先规则，主要是采用一种二分方法，当一列特征有K个类别，第k个类别概率为pk时，其计算Gini系数系数的公式为：

                                                    

对于样本D,如果根据特征A的某个值a,把D分成D1和D2两部分，则在特征A的条件下，Gini系数计算公式为：

                                                

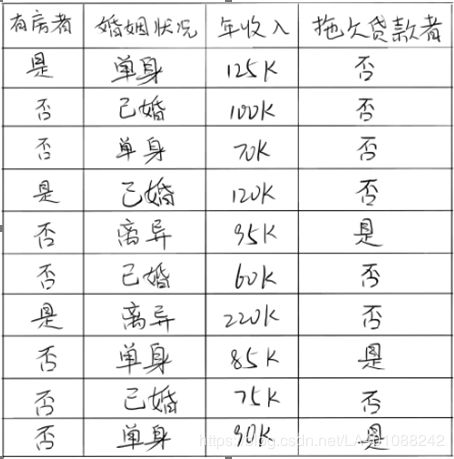
公式大家应该都不能理解，下面我们看一个例子，如图

                                           

在上述图中，属性有3个，分别是有房情况，婚姻状况和年收入，其中有房情况和婚姻状况是离散的取值，而年收入是连续的取值。拖欠贷款者属于分类的结果。

首先对数据集非类标号属性{是否有房，婚姻状况，年收入}分别计算它们的Gini系数增益，取Gini系数增益值最大的属性作为决策树的根节点属性。根节点的Gini系数。

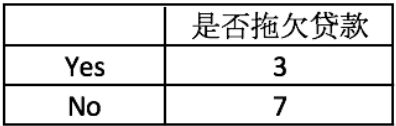
首先，我们先求需要预测标签的Gini系数

                                           

Gini(是否拖欠贷款)=1−(3/10)^2−(7/10)^2=0.42

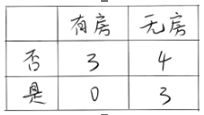
我们开始对是否有房这一列特征求Gini系数

                                                             

Gini(左子节点)=1−(0/3)^2−(3/3)^2=0

Gini(右子节点)=1−(3/7)^2−(4/7)^2=0.4898

Δ{是否有房}=Gini(是否拖欠贷款) - 特征概率*Gini系数= 0.42−7/10×0.4898−3/10×0=0.077

而对于婚姻状况属性来说，它的取值有3种，而我们要进行二分法，所以共有三种情况，按照每种属性值分裂后Gini指标计算如下:

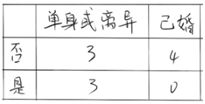
1.当分组为{离异或已婚} | {单身}时

                                                             

 

Δ{婚姻状况}=0.42−4/10×0.5−6/10×[1−(1/6^)2−(5/6)^2]=0.053

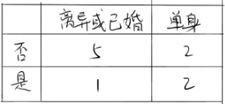
2.当分组为{离异或单身} | {已婚}时

                                                              

Δ{婚姻状况}=0.42−4/10×0−6/10×[1−(3/6)^2−(3/6)^2]=0.12

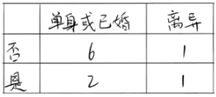
3.当分组为{单身或已婚} | {离异}时

                                                             

Δ{婚姻状况}=0.42−2/10×0.5−8/10×[1−(2/8)^2−(6/8)^2]=0.02

CART回归树

上图第三列特征为连续型回归值，对此一一二分分类求Gini系数可能有些麻烦，所以我们加一步，去求它每一次分裂值两边的方差，然后再根据方差去决定它的最优二分位置，再去计算Gnin系数以及Gini系数增益

Gain_σ计算公式如下：

Gain_σA（S）=  σ(S1) + σ(S2)      注：σ(S1)和σ(S2)为二分后两边数据的方差

1. 根据第1个属性值划分为<=125和>125两部分：

<=125的有：125, 100, 70, 120, 95, 60, 85, 75, 90    均值为91.111

>125的有：220    均值为220

σ(S1) = 61.554

σ(S2) = 0

Gain_σ(S) = σ(S1) + σ(S2) = 61.554

 

2. 根据第2个属性值划分为<=100和>100两部分：

<=100的有：100, 70, 95, 60, 85, 75, 90    均值为82.143

>100的有：125,120,220    均值为155

σ(S1) = 35.254

σ(S2) = 79.687

Gain_σ(S) = σ(S1) + σ(S2) = 114.941

 

3. 根据第3个属性值划分为<=70和>70两部分：

Gain_σ(S) = σ(S1) + σ(S2) =129.085

 

4. 根据第4个属性值划分为<=120和>120两部分：

Gain_σ(S) = σ(S1) + σ(S2) =117.144

 

5. 根据第5个属性值划分为<=95和>95两部分：

Gain_σ(S) = σ(S1) + σ(S2) =122.347

 

6. 根据第6个属性值划分为<=60和>60两部分：

Gain_σ(S) = σ(S1) + σ(S2) =128.798

 

7. 根据第7个属性值划分为<=220和>220两部分：

Gain_σ(S) = σ(S1) + σ(S2) =136.894

 

8. 根据第8个属性值划分为<=85和>85两部分：

Gain_σ(S) = σ(S1) + σ(S2) =126.656

 

9. 根据第9个属性值划分为<=75和>75两部分：

Gain_σ(S) = σ(S1) + σ(S2) =125.568

 

根据第10个属性值划分为<=90和>90两部分：

Gain_σ(S) = σ(S1) + σ(S2) =125.511

通过计算 Gain_σ 可知最优二分点为第一种情况，即125

对其求Gini系数增益

Gini（S1）= 1 - [(6/9)^2+(3/9)^2] = 0.667

Gini（S2）= 1 - [(1/1)^2+(0/1)^2] = 0

Δ{年收入} = 0.42 - 9/10*0.667 - 0 =  -0.1803

到此计算完毕，通过上面的一系列计算，我们可知最优划分特征（即Gini增益最大）为婚姻状况分组为{离异或单身} | {已婚}时为最优划分列