贝塞尔曲线-维基百科
贝塞尔曲线
在数学的数值分析领域中,贝塞尔曲线(英语:Bézier curve)是电脑图形学中相当重要的参数曲线。更高维度的广泛化贝塞尔曲线就称作贝塞尔曲面,其中贝塞尔三角是一种特殊的实例。
贝塞尔曲线于1962年,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau算法开发,以稳定数值的方法求出贝塞尔曲线。
目录
- 1 实例说明
- 1.1 线性贝塞尔曲线
- 1.2 二次方贝塞尔曲线
- 1.3 三次方贝塞尔曲线
- 2 一般化
- 2.1 术语
- 2.2 注解
- 3 建构贝塞尔曲线
- 3.1 线性曲线
- 3.2 二次曲线
- 3.3 高阶曲线
- 4 升阶
- 5 应用
- 5.1 电脑绘图
- 5.2 程式范例
- 6 多项式表示法
- 7 有理贝塞尔曲线
- 8 参阅
- 9 参考文献
- 10 外部链接
实例说明
线性贝塞尔曲线
给定点P0、P1,线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出:
- B ( t ) = P 0 + ( P 1 − P 0 ) t = ( 1 − t ) P 0 + t P 1 , t ∈ [ 0 , 1 ] {\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}+(\mathbf {P} _{1}-\mathbf {P} _{0})t=(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1}{\mbox{ , }}t\in [0,1]}
且其等同于线性插值。
二次方贝塞尔曲线
二次方贝塞尔曲线的路径由给定点P0、P1、P2的函数B(t)追踪:
- B ( t ) = ( 1 − t ) 2 P 0 + 2 t ( 1 − t ) P 1 + t 2 P 2 , t ∈ [ 0 , 1 ] {\displaystyle \mathbf {B} (t)=(1-t)^{2}\mathbf {P} _{0}+2t(1-t)\mathbf {P} _{1}+t^{2}\mathbf {P} _{2}{\mbox{ , }}t\in [0,1]} 。
TrueType字型就运用了以贝塞尔样条组成的二次贝塞尔曲线。
三次方贝塞尔曲线
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P2之前,走向P1方向的“长度有多长”。
曲线的参数形式为:
- B ( t ) = P 0 ( 1 − t ) 3 + 3 P 1 t ( 1 − t ) 2 + 3 P 2 t 2 ( 1 − t ) + P 3 t 3 , t ∈ [ 0 , 1 ] {\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}(1-t)^{3}+3\mathbf {P} _{1}t(1-t)^{2}+3\mathbf {P} _{2}t^{2}(1-t)+\mathbf {P} _{3}t^{3}{\mbox{ , }}t\in [0,1]} 。
现代的成象系统,如PostScript、Asymptote和Metafont,运用了以贝塞尔样条组成的三次贝塞尔曲线,用来描绘曲线轮廓。
一般化
n {\displaystyle n} 阶贝塞尔曲线可如下推断。给定点P0、P1、…、Pn,其贝塞尔曲线即
- B ( t ) = ∑ i = 0 n ( n i ) P i ( 1 − t ) n − i t i = ( n 0 ) P 0 ( 1 − t ) n t 0 + ( n 1 ) P 1 ( 1 − t ) n − 1 t 1 + ⋯ + ( n n − 1 ) P n − 1 ( 1 − t ) 1 t n − 1 + ( n n ) P n ( 1 − t ) 0 t n , t ∈ [ 0 , 1 ] {\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}{n \choose i}\mathbf {P} _{i}(1-t)^{n-i}t^{i}={n \choose 0}\mathbf {P} _{0}(1-t)^{n}t^{0}+{n \choose 1}\mathbf {P} _{1}(1-t)^{n-1}t^{1}+\cdots +{n \choose n-1}\mathbf {P} _{n-1}(1-t)^{1}t^{n-1}+{n \choose n}\mathbf {P} _{n}(1-t)^{0}t^{n}{\mbox{ , }}t\in [0,1]} 。
例如 n = 5 {\displaystyle n=5} :
- B ( t ) = P 0 ( 1 − t ) 5 + 5 P 1 t ( 1 − t ) 4 + 10 P 2 t 2 ( 1 − t ) 3 + 10 P 3 t 3 ( 1 − t ) 2 + 5 P 4 t 4 ( 1 − t ) + P 5 t 5 , t ∈ [ 0 , 1 ] {\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}(1-t)^{5}+5\mathbf {P} _{1}t(1-t)^{4}+10\mathbf {P} _{2}t^{2}(1-t)^{3}+10\mathbf {P} _{3}t^{3}(1-t)^{2}+5\mathbf {P} _{4}t^{4}(1-t)+\mathbf {P} _{5}t^{5}{\mbox{ , }}t\in [0,1]} 。
如上公式可如下递归表达: 用 B P 0 P 1 … P n {\displaystyle \mathbf {B} _{\mathbf {P} _{0}\mathbf {P} _{1}\ldots \mathbf {P} _{n}}} 表示由点P0、P1、…、Pn所决定的贝塞尔曲线。则
- B ( t ) = B P 0 P 1 … P n ( t ) = ( 1 − t ) B P 0 P 1 … P n − 1 ( t ) + t B P 1 P 2 … P n ( t ) {\displaystyle \mathbf {B} (t)=\mathbf {B} _{\mathbf {P} _{0}\mathbf {P} _{1}\ldots \mathbf {P} _{n}}(t)=(1-t)\mathbf {B} _{\mathbf {P} _{0}\mathbf {P} _{1}\ldots \mathbf {P} _{n-1}}(t)+t\mathbf {B} _{\mathbf {P} _{1}\mathbf {P} _{2}\ldots \mathbf {P} _{n}}(t)}
用平常话来说, n {\displaystyle n} 阶的贝塞尔曲线,即双 n − 1 {\displaystyle n-1} 阶贝塞尔曲线之间的插值。
术语
一些关于参数曲线的术语,有
- B ( t ) = ∑ i = 0 n P i b i , n ( t ) , t ∈ [ 0 , 1 ] {\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}\mathbf {P} _{i}\mathbf {b} _{i,n}(t),\quad t\in [0,1]}
即多项式
- b i , n ( t ) = ( n i ) t i ( 1 − t ) n − i , i = 0 , … n {\displaystyle \mathbf {b} _{i,n}(t)={n \choose i}t^{i}(1-t)^{n-i},\quad i=0,\ldots n}
又称作n阶的伯恩斯坦基底多项式,定义00 = 1。
点Pi称作贝塞尔曲线的控制点。多边形以带有线的贝塞尔点连接而成,起始于P0并以Pn终止,称作贝塞尔多边形(或控制多边形)。贝塞尔多边形的凸包(convex hull)包含有贝塞尔曲线。
注解
- 开始于P0并结丛于Pn的曲线,即所谓的端点插值法属性。
- 曲线是直线的充分必要条件是所有的控制点都位在曲线上。同样的,贝塞尔曲线是直线的充分必要条件是控制点共线。
- 曲线的起始点(结丛点)相切于贝塞尔多边形的第一节(最后一节)。
- 一条曲线可在任意点切割成两条或任意多条子曲线,每一条子曲线仍是贝塞尔曲线。
- 一些看似简单的曲线(如圆)无法以贝塞尔曲线精确的描述,或分段成贝塞尔曲线(虽然当每个内部控制点对单位圆上的外部控制点水平或垂直的的距离为 4 ( 2 − 1 ) / 3 {\displaystyle 4\left({\sqrt {2}}-1\right)/3} 时,分成四段的贝塞尔曲线,可以小于千分之一的最大半径误差近似于圆)。
- 位于固定偏移量的曲线(来自给定的贝塞尔曲线),又称作偏移曲线(假平行于原来的曲线,如两条铁轨之间的偏移)无法以贝塞尔曲线精确的形成(某些平凡实例除外)。无论如何,现存的启发法通常可为实际用途中给出近似值。
建构贝塞尔曲线
线性曲线
![线性贝塞尔曲线演示动画,t在[0,1]区间](http://img.e-com-net.com/image/info8/48b69bbf13904451b1050c78033f1d04.gif) |
| 线性贝塞尔曲线演示动画,t在[0,1]区间 |
线性贝塞尔曲线函数中的t会经过由P0至P1的B(t)所描述的曲线。例如当t=0.25时,B(t)即一条由点P0至P1路径的四分之一处。就像由0至1的连续t,B(t)描述一条由P0至P1的直线。
二次曲线
为建构二次贝塞尔曲线,可以中介点Q0和Q1作为由0至1的t:
- 由P0至P1的连续点Q0,描述一条线性贝塞尔曲线。
- 由P1至P2的连续点Q1,描述一条线性贝塞尔曲线。
- 由Q0至Q1的连续点B(t),描述一条二次贝塞尔曲线。
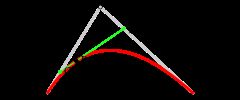 |
||
| 二次贝塞尔曲线的结构 | 二次贝塞尔曲线演示动画,t在[0,1]区间 |
高阶曲线
为建构高阶曲线,便需要相应更多的中介点。对于三次曲线,可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2,和由二次曲线描述的点R0、R1所建构:
 |
![三次贝塞尔曲线演示动画,t in [0,1]](http://img.e-com-net.com/image/info8/eff5d9e1eacd4a4cbb0fc0348053feab.gif) |
|
| 三次贝塞尔曲线的结构 | 三次贝塞尔曲线演示动画,t在[0,1]区间 |
对于四次曲线,可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2、Q3,由二次贝塞尔曲线描述的点R0、R1、R2,和由三次贝塞尔曲线描述的点S0、S1所建构:
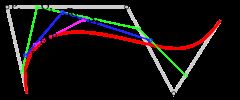 |
![四次贝塞尔曲线演示动画,t in [0,1]](http://img.e-com-net.com/image/info8/480fd9f70f0348a9ba52c16d0b013051.gif) |
|
| 四次贝塞尔曲线的结构 | 四次贝塞尔曲线演示动画,t在[0,1]区间 |
还可参阅五阶贝塞尔曲线的构成:
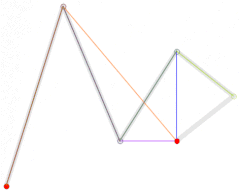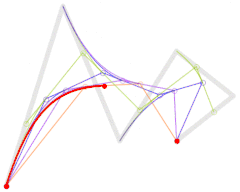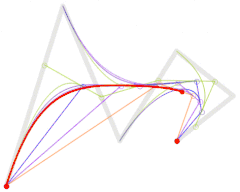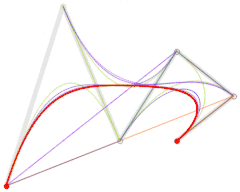 |
| 五次贝塞尔曲线演示动画,t在[0,1]区间 |
这些运动轨迹使用de Casteljau算法计算出贝塞尔曲线。[1]
升阶
n次贝塞尔曲线可以转换为一个形状完全相同的n+1次贝塞尔曲线。 这在软件只支援特定阶次的贝塞尔曲线时很有用。 例如,Cairo只支援三次贝塞尔曲线,你就可以用升阶的方法在Cairo画出二次贝塞尔曲线。
我们利用 B ( t ) = ( 1 − t ) B ( t ) + t B ( t ) {\displaystyle \mathbf {B} (t)=(1-t)\mathbf {B} (t)+t\mathbf {B} (t)} 这个特性来做升阶。我们把曲线方程式中每一项 b i , n ( t ) P i {\displaystyle \mathbf {b} _{i,n}(t)\mathbf {P} _{i}} 都乘上 (1 − t) 或 t,让每一项都往上升一阶。以下是将二阶升为三阶的范例
- ( 1 − t ) 2 P 0 + 2 ( 1 − t ) t P 1 + t 2 P 2 = ( 1 − t ) 3 P 0 + ( 1 − t ) 2 t P 0 + 2 ( 1 − t ) 2 t P 1 + 2 ( 1 − t ) t 2 P 1 + ( 1 − t ) t 2 P 2 + t 3 P 2 = ( 1 − t ) 3 P 0 + 3 ( 1 − t ) 2 t P 0 + 2 P 1 3 + 3 ( 1 − t ) t 2 2 P 1 + P 2 3 + t 3 P 2 {\displaystyle {\begin{aligned}&{}\quad (1-t)^{2}\mathbf {P} _{0}+2(1-t)t\mathbf {P} _{1}+t^{2}\mathbf {P} _{2}\\&=(1-t)^{3}\mathbf {P} _{0}+(1-t)^{2}t\mathbf {P} _{0}+2(1-t)^{2}t\mathbf {P} _{1}\\&{}\qquad +2(1-t)t^{2}\mathbf {P} _{1}+(1-t)t^{2}\mathbf {P} _{2}+t^{3}\mathbf {P} _{2}\\&=(1-t)^{3}\mathbf {P} _{0}+3(1-t)^{2}t{\frac {\mathbf {P} _{0}+2\mathbf {P} _{1}}{3}}+3(1-t)t^{2}{\frac {2\mathbf {P} _{1}+\mathbf {P} _{2}}{3}}+t^{3}\mathbf {P} _{2}\end{aligned}}}
对任何的n值,我们都可以使用以下等式
- ( n + 1 i ) ( 1 − t ) b i , n = ( n i ) b i , n + 1 , ( 1 − t ) b i , n = n + 1 − i n + 1 b i , n + 1 {\displaystyle {n+1 \choose i}(1-t)\mathbf {b} _{i,n}={n \choose i}\mathbf {b} _{i,n+1},\quad (1-t)\mathbf {b} _{i,n}={\frac {n+1-i}{n+1}}\mathbf {b} _{i,n+1}}
- ( n + 1 i + 1 ) t b i , n = ( n i ) b i + 1 , n + 1 , t b i , n = i + 1 n + 1 b i + 1 , n + 1 {\displaystyle {n+1 \choose i+1}t\mathbf {b} _{i,n}={n \choose i}\mathbf {b} _{i+1,n+1},\quad t\mathbf {b} _{i,n}={\frac {i+1}{n+1}}\mathbf {b} _{i+1,n+1}}
- B ( t ) = ( 1 − t ) ∑ i = 0 n b i , n ( t ) P i + t ∑ i = 0 n b i , n ( t ) P i = ∑ i = 0 n n + 1 − i n + 1 b i , n + 1 ( t ) P i + ∑ i = 0 n i + 1 n + 1 b i + 1 , n + 1 ( t ) P i = ∑ i = 0 n + 1 ( i n + 1 P i − 1 + n + 1 − i n + 1 P i ) b i , n + 1 ( t ) = ∑ i = 0 n + 1 b i , n + 1 ( t ) P ′ i {\displaystyle {\begin{aligned}\mathbf {B} (t)&=(1-t)\sum _{i=0}^{n}\mathbf {b} _{i,n}(t)\mathbf {P} _{i}+t\sum _{i=0}^{n}\mathbf {b} _{i,n}(t)\mathbf {P} _{i}\\&=\sum _{i=0}^{n}{\frac {n+1-i}{n+1}}\mathbf {b} _{i,n+1}(t)\mathbf {P} _{i}+\sum _{i=0}^{n}{\frac {i+1}{n+1}}\mathbf {b} _{i+1,n+1}(t)\mathbf {P} _{i}\\&=\sum _{i=0}^{n+1}\left({\frac {i}{n+1}}\mathbf {P} _{i-1}+{\frac {n+1-i}{n+1}}\mathbf {P} _{i}\right)\mathbf {b} _{i,n+1}(t)=\sum _{i=0}^{n+1}\mathbf {b} _{i,n+1}(t)\mathbf {P'} _{i}\end{aligned}}}
式中 P − 1 {\displaystyle \mathbf {P} _{-1}} 和 P n + 1 {\displaystyle \mathbf {P} _{n+1}} 可以任意挑选。
因此,新的控制点为[2]
- P ′ i = i n + 1 P i − 1 + n + 1 − i n + 1 P i , i = 0 , … , n + 1. {\displaystyle \mathbf {P'} _{i}={\frac {i}{n+1}}\mathbf {P} _{i-1}+{\frac {n+1-i}{n+1}}\mathbf {P} _{i},\quad i=0,\ldots ,n+1.}
应用
电脑绘图
由于需要点阵化更精细的分辨率时,重新插值(补点)的计算量较小,贝塞尔曲线被广泛地在计算机图形中用来为平滑曲线建立模型。贝塞尔曲线是矢量图形文件和相应软件(如PostScript、PDF等)能够处理的唯一曲线,用于光滑地近似其他曲线。
二次和三次贝塞尔曲线最为常用。
程式范例
下列程式码为一简单的实际运用范例,展示如何使用C语言标出三次方贝塞尔曲线。注意,此处仅简单的计算多项式系数,并读尽一系列由0至1的t值;实践中一般不会这么做,递归求解通常会更快速——以更多的内存为代价,花费较少的处理器时间。不过直接的方法较易于理解并产生相同结果。以下程式码已使运算更为清晰。实践中的最优化会先计算系数一次,并在实际计算曲线点的循环中反复使用。此处每次都会重新计算,损失了效率,但程式码更清楚易读。
曲线的计算可在曲线阵列上将相连点画上直线——点越多,曲线越平滑。
在部分架构中,下以程式码也可由动态规划进行最优化。举例来说,dt是一个常数,cx * t则等同于每次反复就修改一次常数。经反复应用这种最优化后,循环可被重写为没有任何乘法(虽然这个过程不是稳定数值的)。
/*
產生三次方貝茲曲線的程式碼
*/
typedef struct
{
float x;
float y;
}
Point2D;
/*
cp在此是四個元素的陣列:
cp[0]為起始點,或上圖中的P0
cp[1]為第一個控制點,或上圖中的P1
cp[2]為第二個控制點,或上圖中的P2
cp[3]為結束點,或上圖中的P3
t為參數值,0 <= t <= 1
*/
Point2D PointOnCubicBezier( Point2D* cp, float t )
{
float ax, bx, cx;
float ay, by, cy;
float tSquared, tCubed;
Point2D result;
/*計算多項式係數*/
cx = 3.0 * (cp[1].x - cp[0].x);
bx = 3.0 * (cp[2].x - cp[1].x) - cx;
ax = cp[3].x - cp[0].x - cx - bx;
cy = 3.0 * (cp[1].y - cp[0].y);
by = 3.0 * (cp[2].y - cp[1].y) - cy;
ay = cp[3].y - cp[0].y - cy - by;
/*計算位於參數值t的曲線點*/
tSquared = t * t;
tCubed = tSquared * t;
result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;
result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;
return result;
}
/*
ComputeBezier以控制點cp所產生的曲線點,填入Point2D結構的陣列。
呼叫者必須分配足夠的記憶體以供輸出結果,其為
另一种贝塞尔曲线的应用是在动画中,描述物件的运动路径等等。此处,曲线的x、y位置不用来标示曲线,但用来表示图形位置。当用在这种形式时,连续点之间的距离会变的更为重要,且大多不是平均比例。点将会串的更紧密,控制点更接近每一个点,而更为稀疏的控制点会散的更开。如果需要线性运动速度,进一步处理时就需要循所需路径将点平均分散。
多项式表示法
有时我们可能想要把贝塞尔曲线表示为多项式,而非比较不直接的伯恩斯坦多项式。使用二项式定理和贝塞尔曲线的定义,重新整理后可以得到:
- B ( t ) = ∑ j = 0 n t j C j {\displaystyle \mathbf {B} (t)=\sum _{j=0}^{n}{t^{j}\mathbf {C} _{j}}}
此处
- C j = n ! ( n − j ) ! ∑ i = 0 j ( − 1 ) i + j P i i ! ( j − i ) ! = ∏ m = 0 j − 1 ( n − m ) ∑ i = 0 j ( − 1 ) i + j P i i ! ( j − i ) ! . {\displaystyle \mathbf {C} _{j}={\frac {n!}{(n-j)!}}\sum _{i=0}^{j}{\frac {(-1)^{i+j}\mathbf {P} _{i}}{i!(j-i)!}}=\prod _{m=0}^{j-1}(n-m)\sum _{i=0}^{j}{\frac {(-1)^{i+j}\mathbf {P} _{i}}{i!(j-i)!}}.}
计算曲线上的点时需要多次计算 B ( t ) {\displaystyle \mathbf {B} (t)} ,因此事先计算好 C j {\displaystyle \mathbf {C} _{j}} 会比较实际;然而要小心高阶曲线可能会缺乏数值稳定性(需使用De Casteljau算法来处理)。注意其empty product为1。
有理贝塞尔曲线
有理贝塞尔增加可调节的权重,以提供更近似于随意的形状。分子是加权的伯恩斯坦形式贝塞尔曲线,而分母是加权的伯恩斯坦多项式的总和。
给定n + 1控制点Pi,有理贝塞尔曲线可如下描述:
- B ( t ) = ∑ i = 0 n b i , n ( t ) P i w i ∑ i = 0 n b i , n ( t ) w i {\displaystyle \mathbf {B} (t)={\frac {\sum _{i=0}^{n}b_{i,n}(t)\mathbf {P} _{i}w_{i}}{\sum _{i=0}^{n}b_{i,n}(t)w_{i}}}}
或简单的
- B ( t ) = ∑ i = 0 n ( n i ) t i ( 1 − t ) n − i P i w i ∑ i = 0 n ( n i ) t i ( 1 − t ) n − i w i {\displaystyle \mathbf {B} (t)={\frac {\sum _{i=0}^{n}{n \choose i}t^{i}(1-t)^{n-i}\mathbf {P} _{i}w_{i}}{\sum _{i=0}^{n}{n \choose i}t^{i}(1-t)^{n-i}w_{i}}}}
参阅
- de Casteljau算法
- 样条
- 贝塞尔样条
- 贝塞尔曲面
- 贝塞尔三角
- NURBS
- string art,Bézier curves are also formed by many common forms of string art, where strings are looped across a frame of nails.
- 埃尔米特曲线
参考文献
- Paul Bourke: Bézier curves, http://astronomy.swin.edu.au/~pbourke/curves/bezier/
- Donald Knuth: Metafont: the Program, Addison-Wesley 1986, pp. 123-131. Excellent discussion of implementation details; available for free as part of the TeX distribution.
- Dr Thomas Sederberg, BYU Bézier curves, http://www.tsplines.com/resources/class_notes/Bezier_curves.pdf
- J.D. Foley et al.: Computer Graphics: Principles and Practice in C (2nd ed., Addison Wesley, 1992)
- ^ Shene, C.K. Finding a Point on a Bézier Curve: De Casteljau's Algorithm. [6 September 2012].
- ^ Farin, Gerald, Curves and surfaces for computer-aided geometric design 4, Elsevier Science & Technology Books, 1997, ISBN 978 0 12249054 5

