文档图像倾斜角检测及校正（二）（Matlab）

文档图像倾斜角检测及校正（二）

• 最小距离法直线拟合原理
• Matlab程序

---

阅读之前注意：

Hi，你好，我是Cooper Liu，欢迎来到我写的“文档图像校正”系列博客。基于三种原理，我写了四个实验性的Matlab验证程序，以及两个文档校正Matlab程序。在这里你将能够获取所有的源代码以及测试图片，完全可以在你自己的Matlab上跑这些程序。

如果你是学生，请注意不要抄袭，课程设计作业的话，这种程序仅仅只能让你得到80%左右的成绩。
如果你是工作人士或者只是感兴趣的极客，Okay，我想这些程序对于理解原理是如何应用为程序的已经足够 。

最后，请勿将这些资源用于商业用途（如你所见，这些程序都非常的初级）或者是谋取个人利益，知识在传播的过程中能展现更大的价值^-

本文阅读建议用时：32min
本文阅读结构如下表：

项目	下属项目	测试用例数量
最小距离法直线拟合原理	无	0
Matlab程序	无	1

最小距离法直线拟合原理¹

最小距离法拟合直线是指，我们设线条上n个特征点：
$$(x_i,y_i),i=1,2,\dots ,n，$$则第i个特征点到直线 $y=kx+b$ 的垂直距离为：
$$\frac{|y_i-(k{x}_i+b)|}{\sqrt{(1+k^2)}}$$因此n个特征点到直线 $y=kx+b$ 的距离平方和为：
$$D(k,b)=\sum _{i=1}^n\frac{[y_i-(k{x}_i+b){]}^2}{1+k^2}=\frac{1}{1+k^2}\sum _{i=1}^n[y_i-(k{x}_i+b){]}^2$$如果存在$k_d,b_d$使得：
$$D(k_d,b_d)=\underset{k,b}{\min }D(k,b)$$
则称$k_d,b_d$为$k,b$的最小距离估计，此方法称为最小距离法。
为了计算和叙述的方便，我们引入以下的记号：
$$\bar{x}=\frac{1}{n}\sum _{i=1}^n{x}_i\bar{y}=\frac{1}{n}\sum _{i=1}^n{y}_i{L}_{xx}=\sum _{i=1}^n(x_i-\bar{x}{)}^2{L}_{yy}=\sum _{i=1}^n(y_i-\bar{y}{)}^2$$$$L_{xy}=\sum _{i=1}^n(x_i-\bar{x})(y_i-\bar{y})$$利用极值法求得：$b_d=y-k\bar{x}，k_d=\frac{L_{yy}-L_{xx}+\sqrt{(L_{yy}-L_{xx}{)}^2+4L_{xy}^2}}{2L_{xy}}$
所以文档的倾斜角为：${\alpha }_d=arctan(k_d)$

Matlab程序

基于以上原理，我编写了Matlab程序来进行实验，源代码可以参考angleDetection2.m文件。测试图片为line5.bmp。²
测试图片可以从这里获取，链接：https://pan.baidu.com/s/1dGmmGjn 密码：okt3

以下是实验结果：

如果您不想打开新的页面查看matlab源代码，也可以直接参考以下代码：

%%本版基于最小距离法直线拟合原理 
%%2018.01.19 by Cooper Liu
%%Questions? Contact me: [email protected]
clear;clc; %清空之前的变量
I=imread('line5.bmp'); %读取图像
level=graythresh(I); %使用最大类间方差法找到图片的一个合适的阈值
bw=im2bw(I,level); %根据阈值，使用im2bw函数将灰度图像转换为二值图像时
figure(1);imshow(bw);

[m,n]=size(bw); %获取尺寸
xSum=0;xCount=0;
ySum=0;yCount=0;
tic; %计时开始
for i=1:m
    for j=1:n
        if bw(i,j)==0
           xSum=xSum+i;xCount=xCount+1;
           ySum=ySum+j;yCount=yCount+1;
        end
    end
end
xMean=xSum/xCount;
yMean=ySum/yCount;

Lxx=0;
Lyy=0;
Lxy=0;
for i=1:m
    for j=1:n
        if bw(i,j)==0
          Lxx=Lxx+(i-xMean)^2;
          Lyy=Lyy+(j-yMean)^2;
          Lxy=Lxy+(i-xMean)*(j-yMean);
        end
    end
end
toc %获取计时时间
tmp=((Lyy-Lxx) + nthroot((Lyy-Lxx)^2 + 4*Lxy^2, 2))/(2*Lxy);
if isnan(tmp) 
    tmp=inf; %如果求得tmp是NaN，那么不需要旋转
end
%tmp=atan(2*Lxy/(Lxx-Lyy))/2; %如果倾斜角相对于水平超过正负45
angle=atan(tmp); %用atan求出来的角度在-pi/2到+pi/2之间
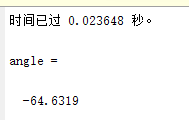
angle=angle*180/pi

rot=90-angle;
pic=imrotate(I,rot,'crop'); %旋转图像
figure(2);imshow(pic);

---

1. 参考文献：[1] 荆雷，张欣，郭金鑫．基于版面的拍照文档图像倾斜校正.激光与红外[J]．2010，第10期 ↩︎

2. 同时感谢愿意在网络上分享自己想法的各位博主。 ↩︎