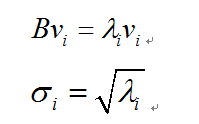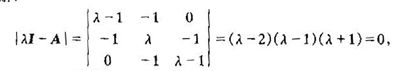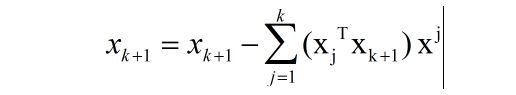机器学习之奇异值分解之特征值（SVD）

   MIT教授Gilbert Strang曾经称SVD为线性代数的绝对制高点，其在单机上实现就是一个很困难的问题，更何况于分布式？当然这里所指的实现并不是指能够做出来，而是指能够给社会带来真正贡献，毕竟算法这东西，做出来后如果精度不高，时间和空间复杂度不够好，那么就不可能运用于商业和各种工程中。当然，数学之美中吴军老师简要的谈了谈Google实现的SVD，称其是对人类的一个大贡献。

   从前面的文章中，我们可以得到重要的信息，矩阵的奇异值和特征值之间存在非常重要的联系：

                                                                                                           

  故而从某种意义上，我们可以从矩阵的特征值开始研究如何求解矩阵的奇异值。对于大规模矩阵而言，矩阵的特征值求解一般采用迭代的思想，而不采用曾经我们说熟悉的矩阵特征值的求解方法，比如行列式方法：

  比如存在一个矩阵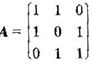，那么我们正规的方法则是采用行列式的方法来求得其特征值：

但是呢？对于大规模的矩阵而言，这种方式是不恰当的，其一是矩阵规模越大，这个式子将会特别的长，计算起来的时间和空间复杂度都将可能达到计算机无法承受的地步。其二是，受限于计算机的精度问题，计算机一般保存数据是64位，还是128位？这样的精度在计算这个式子时很容易出现有限精度的误差，最终可能导致求出来的特征值和原特征值差距很大，求解失败。

那么对于求解大规模矩阵特征值而言，我们可以采取什么方式进行了？

方法还是蛮多的，但是要找到一个合适于所给的具体的矩阵的方法则是需要我们自己去研究和判断的，针对具体的问题要具体分析。接下来我来例举下现在常用的各种矩阵特征值的数值计算方法（具体的就不写了，毕竟方法太多，当然笔者使用的方法还是会简略介绍下）：

在介绍具体的矩阵特征值和特征向量的求解方法前，我想有必要了解一下Givens 旋转变换：（下图截取自中国科学技术大学数学系授课PPT）

从上图中，我们可以看到曾经我们所熟悉的旋转变换的影子，旋转变换将一个图形在一个坐标系中进行旋转，而上图也是类似的思想，通过一定的构造方法将矩阵中一些非对角元的元素化为零元素。这是一种很有效的策略，后面一些方法会用到这个有效的变换。（具体可参考：http://zh.wikipedia.org/wiki/吉文斯旋转）

1.雅克比方法：最古老的方法，收敛速度较慢，精度较高，适合并行化，也有很多的改进方法，使收敛的速度变快。

   其基本的迭代形式为：（k代表迭代次数，k=1,2,3……，其中往往Q选择Givens旋转变换）                      

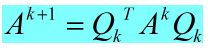
（具体可参考：http://zh.wikipedia.org/wiki/雅可比法

http://blog.csdn.net/xiaowei_cqu/article/details/8585703）

2.Rayleigh商迭代：利用Rayleigh商作为位移的反迭代，一般具有三次收敛性（其基本算法描述如下）：

当然对于该种方法而言，有很多的改进和加速技术，详细的笔者也不是很清楚。

（一些资料：http://blog.csdn.net/archielau/article/details/7636132

另外，据说MIT的开放课程不错，可以网上搜搜。）

3.QR方法：

首先我们来看看其运算量：

从上述的运算量，我们可以看出，针对不同的矩阵（普通矩阵或三对角矩阵）和不同的策略（只要求特征值问题和还需要对应特征向量问题）其复杂度是完全不同的。首先，我们从普通的对称矩阵开始，理解下什么是QR迭代算法。

QR迭代算法依赖QR分解，一个好的QR分解可以使迭代运算量大大下降。

QR分解是一种将矩阵A分解成上三角矩阵和正交矩阵的分解方法：

                                                                                           A=QR（Q为正交阵，R为上三角矩阵）

其分解方法有很多，每一种方法都有其优势和不足：

（1）Givens旋转方法，适合矩阵稀疏的情况，如三对角矩阵。>>上面的QR迭代计算三对角矩阵时间复杂度底而Givens旋转变换又很适合QR方法，这样的组合是不是很诱人。

 （2）Householder变换，适合于一般矩阵。

具体参考：http://wenku.baidu.com/view/952493d2195f312b3169a538.html

                    http://zh.wikipedia.org/wiki/豪斯霍尔德变换

（3）Gram-Schmidt正交化：一种较为普通的方法，运算量较大

具体参考：Gram-Schmidt正交化，这里比较详细。但总的来说，可以归纳为一个式子：

好的，通过QR分解我们就可以进行QR迭代啦！QR迭代的基本形式为（不断进行如下方式的迭代，最终逼近近似的对角矩阵，迭代结束）：

具体的过程，移位加速迭代后续博客将会更新，这里只讲基本形式。

（参考资料：http://wenku.baidu.com/view/33005d0c79563c1ec5da71c7.html）

4.分而治之方法：计算对称三对角矩阵的特征值和特征值向量的一种快速算法. 基本思想是将大矩阵分解成小矩阵, 然后利用递推思想求特征值. 在最坏的情形下, 运算量为O(n3),但在实际应用中, 平均为O(n2:3). 如果使用快速多极子算法(FMM) 后, 理论上的运算量可降低到O(n logp n), 其中p 是一个较小的整数, 这使得分而治之算法成为目前求解n > 25 的对称三对角矩阵的特征值和特征向量的最快的方法.

传说中的高大上方法，当然即使雅克比方法也有许多的改进策略，使其迭代速度大大提升。

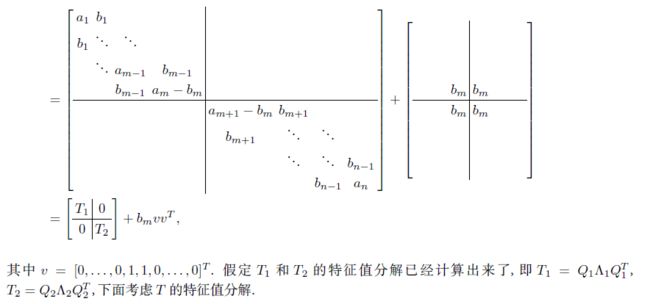
我用截取的两张图片来说明分而治之的基本思想：

哈哈，我们又再次进入了三对角矩阵，其实没错，实现SVD很多东西都是围绕着三对角矩阵进行，后续博文更新如何三对角化等内容。

5.求特征的方法还有很多，有兴趣的同学不妨自己动手找些资料，慢慢研究，比如常见的还有对分法等。

好的，此次博文就写到这里你，推荐大家一本书籍：

《数学之美》 作者：吴军                     这本书教我们如何运用我们简单高效的数学知识去解答工程问题，原来我们大学学习过的数学知识这么有用，哈哈。

另外，关于本文的一些理论，可以查阅以下书籍：

《矩阵计算》    Gene H. Golub (1932－2007) 美国科学院、工程院和艺术科学院院士，世界著名的数值分析专家，现代矩阵计算的奠基人，生前曾任斯坦福大学教授。 

                            Charles F. Van Loan 著名数值分析专家。美国康奈尔大学教授，曾任该校计算机科学系主任。

Gene H. Golub和Charles F. Van Loan著   科学出版社出版  （同时也是中国科学院研究生教程读物）

《应用数值线性代数》      James  W.Demmel著    王国荣译

限于笔者水平，上述内容难免出错，还望大家多多指正。