机器学习实战笔记-利用K均值聚类算法对未标注数据分组
聚类是一种无监督的学习,它将相似的对象归到同一个簇中。它有点像全自动分类。聚类方法几乎可以应用于所有对象,簇内的对象越相似,聚类的效果越好
簇识别给出聚类结果的含义。假定有一些数据,现在将相似数据归到一起,簇识别会告诉我们这些簇到底都是些什么。聚类与分类的最大不同在于,分类的目标事先巳知,而聚类则不一样。因为其产生
的结果与分类相同,而只是类别没有预先定义,聚类有时也被称为无监督分类(unsupervised classification )。
聚类分析试图将相似对象归人同一簇,将不相似对象归到不同簇。相似这一概念取决于所选择的相似度计算方法
10.1K-均值聚类算法
K-均值聚类
优点:容易实现。
缺点:可能收敛到局部最小值,在大规模数据集上收敛较慢。
适用数据类型:数值型数据。
K-均值是发现给定数据集的k个簇的算法。簇个数k是用户给定的,每一个簇通过其质心( centroid) , 即簇中所有点的中心来描述。
K-均值算法的工作流程是这样的。首先,随机确定k个初始点作为质心。然后将数据集中的每个点分配到一个簇中,具体来讲,为每个点找距其最近的质心,并将其分配给该质心所对应的簇。这一步完成之后,每个簇的质心更新为该簇所有点的平均值。
上述过程的伪代码表示如下:
创建k个点作为起始质心(经常是随机选择)
当任意一个点的簇分配结果发生改变时
对数据集中的每个数据点
对每个质心
计算质心与数据点之间的距离
将数据点分配到距其最近的簇
对每一个簇,计算簇中所有点的均值并将均值作为质心
K-均值聚类的一般流程
(1)收集数据:使用任意方法。
⑵准备数据:需要数值型数据来计算距离,也可以将标称型数据映射为二值型数据再用于距离计算。
(3)分析数据:使用任意方法。
(4)训练算法:不适用于无监督学习,即无监督学习没有训练过程。
(5)测试算法:应用聚类算法、观察结果。可以使用量化的误差指标如误差平方和(后面会介绍)来评价算法的结果。
(6)使用算法:可以用于所希望的任何应用。通常情况下,簇质心可以代表整个簇的数据来做出决策。
K-均值聚类支持函数(即完成K均值聚类的一些辅助函数),代码如下:
from numpy import *
#general function to parse tab -delimited floats
#assume last column is target value
def loadDataSet(fileName):
dataMat = []
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
#笔者使用的是python3,需要将map映射后的结果转化为list
#map all elements to float()
fltLine = list(map(float,curLine))
dataMat.append(fltLine)
return dataMat
#样本距离计算函数
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB)
#创建簇中心矩阵,初始化为k个在数据集的边界内随机分布的簇中心
def randCent(dataSet, k):
n = shape(dataSet)[1]
#create centroid mat
centroids = mat(zeros((k,n)))
#create random cluster centers, within bounds of each dimension
for j in range(n):
#求出数据集中第j列的最小值(即第j个特征)
minJ = min(dataSet[:,j])
#用第j个特征最大值减去最小值得出特征值范围
rangeJ = float(max(dataSet[:,j]) - minJ)
#创建簇矩阵的第J列,random.rand(k,1)表示产生(10,1)维的矩阵,其中每行值都为0-1中的随机值
#可以这样理解,每个centroid矩阵每列的值都在数据集对应特征的范围内,那么k个簇中心自然也都在数据集范围内
centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))
return centroidsK -均值聚类算法,代码如下:
#distMeas为距离计算函数
#createCent为初始化随机簇心函数
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
m = shape(dataSet)[0]
#create mat to assign data points to a centroid, also holds SE of each point
#创建一个(m,2)维矩阵,第一列存储每个样本对应的簇心,第二列存储样本到簇心的距离
clusterAssment = mat(zeros((m,2)))
#用createCent()函数初始化簇心矩阵
centroids = createCent(dataSet, k)
#保存迭代中clusterAssment是否更新的状态,如果未更新,那么退出迭代,表示收敛
#如果更新,那么继续迭代,直到收敛
clusterChanged = True
while clusterChanged:
clusterChanged = False
#for each data point assign it to the closest centroid
#对每个样本找出离样本最近的簇心
for i in range(m):
#minDist保存最小距离
#minIndex保存最小距离对应的簇心
minDist = inf; minIndex = -1
#遍历簇心,找出离i样本最近的簇心
for j in range(k):
distJI = distMeas(centroids[j,:],dataSet[i,:])
if distJI < minDist:
minDist = distJI; minIndex = j
#如果clusterAssment更新,表示对应样本的簇心发生变化,那么继续迭代
if clusterAssment[i,0] != minIndex: clusterChanged = True
#更新clusterAssment,样本到簇心的距离
clusterAssment[i,:] = minIndex,minDist**2
print(centroids)
#遍历簇心,更新簇心为对应簇中所有样本的均值
for cent in range(k):#recalculate centroids
#利用数组过滤找出簇心对应的簇(数组过滤真是好东西!)
ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#get all the point in this cluster
#对簇求均值,赋给对应的centroids簇心
centroids[cent,:] = mean(ptsInClust, axis=0) #assign centroid to mean
return centroids, clusterAssment代码测试截图如下:
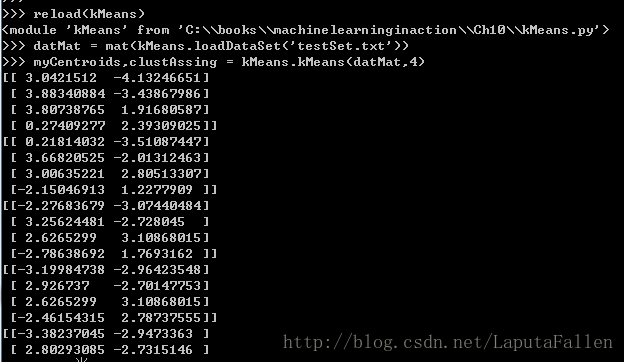
绘制测试截图:

paint函数为笔者写的绘图函数:
def paint(xArr,yArr,xArr1,yArr1):
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xArr,yArr,c='blue')
ax.scatter(xArr1,yArr1,c='red')
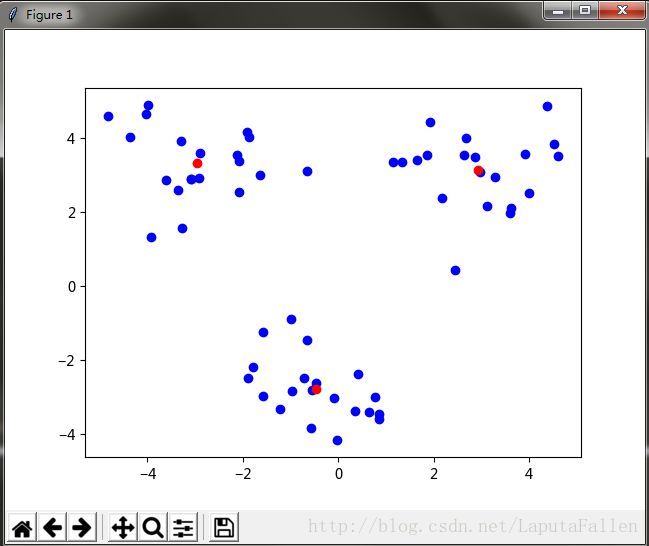
plt.show()效果如下(其中红色的点为簇心):
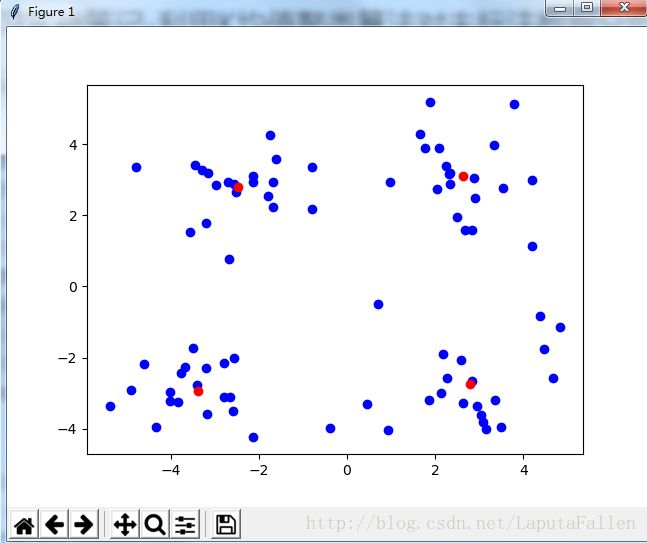
可以看到,经过3次迭代之后K-均值算法收敛
10.2 使用后处理来提高聚类性能
考虑图10-2中的聚类结果,这是在一个包含三个簇的数据集上运行K-均值算法之后的结果,但是点的簇分配结果值没有那么准确。K-均值算法收敛但聚类效果较差的原因是,K-均值算法收敛到了局部最小值,而非全局最小值(局部最小值指结果还可以但并非最好结果,全局最小值是可能的最好结果)。
一种用于度量聚类效果的指标是SSE(Sum of Squared Error,误差平方和),对应clusterAssment矩阵的第一列之和。SSE值越小表示数据点越接近于它们的质心,聚类效果也越好。因为对误差取了平方,因此更加重视那些远离中心的点。一种肯定可以降低SSE值的方法是增加簇的个数,但这违背了聚类的目标。聚类的目标是在保持簇数目不变的情况下提高簇的质量。
那么如何对结果进行改进?你可以对生成的簇进行后处理,一种方法是将具有最大SSE值的簇划分成两个簇。具体实现时可以将最大簇包含的点过滤出来并在这些点上运行K-均值聚类算法,其中的K为2。
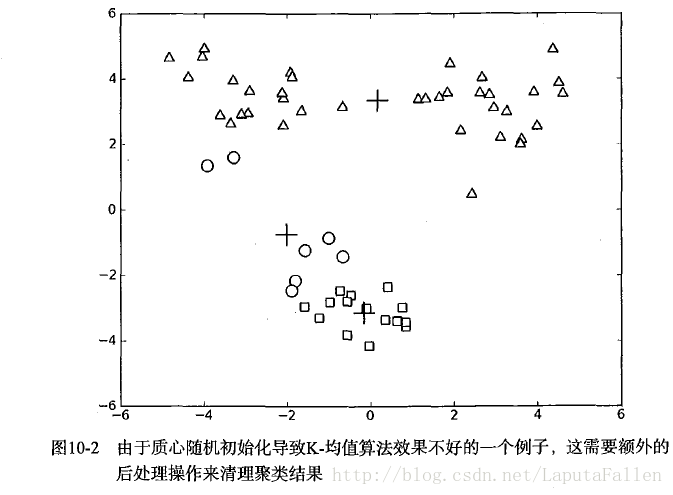
为了保持簇总数不变,可以将某两个簇进行合并。从图10-2中很明显就可以看出,应该将图下部两个出错的簇质心进行合并。可以很容易对二维数据上的聚类进行可视化,但是如果遇到40维的数据应该如何去做?
有两种可以量化的办法:合并最近的质心,或者合并两个使得SSE增幅最小的质心。第一种思路通过计算所有质心之间的距离,然后合并距离最近的两个点来实现。第二种方法需要合并两个簇然后计算总SSE值。必须在所有可能的两个簇上重复上述处理过程,直到找到合并最佳的两个簇为止。接下来将讨论利用上述簇划分技术得到更好的聚类结果的方法。
10.3 二分K-均值算法
为克服K-均值算法收敛于局部最小值的问题,有人提出了另一个称为二分K均值(bisectingK-means)的算法, 该算法首先将所有点作为一个簇,然后将该簇一分为二。之后选择其中一个簇继续进行划分,选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值。上述基于SSE的划分过程不断重复,直到得到用户指定的簇数目为止。
二分K-均值算法的伪代码形式如下:
将所有点看成一个簇
当簇数目小于k时
对于每一个簇
计算总误差
在给定的簇上面进行K-均值聚类(k=2)
计算将该簇一分为二之后的总误差
选择使得误差最小的那个簇进行划分操作
另一种做法是选择SSE最大的簇进行划分,直到簇数目达到用户指定的数目为止。这个做法听起来并不难实现。下面就来看一下该算法的实际效果。
二分K均值聚类算法,代码如下:
#distMeas为距离计算函数
def biKmeans(dataSet, k, distMeas=distEclud):
m = shape(dataSet)[0]
#(m,2)维矩阵,第一列保存样本所属簇,第二列保存样本到簇中心的距离
clusterAssment = mat(zeros((m,2)))
#取数据集特征均值作为初始簇中心
centroid0 = mean(dataSet, axis=0).tolist()[0]
#centList保存簇中心数组,初始化为一个簇中心
#create a list with one centroid
centList =[centroid0]
#calc initial Error
for j in range(m):
clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
#迭代,直到簇中心集合长度达到k
while (len(centList) < k):
#初始化最小误差
lowestSSE = inf
#迭代簇中心集合,找出找出分簇后总误差最小的那个簇进行分解
for i in range(len(centList)):
#get the data points currently in cluster i
#获取属于i簇的数据集样本
ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]
#对该簇进行k均值聚类
centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
#获取该簇分类后的误差和
sseSplit = sum(splitClustAss[:,1])#compare the SSE to the currrent minimum
#获取不属于该簇的样本集合的误差和,注意矩阵过滤中用的是!=i
sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])
#打印该簇分类后的误差和和不属于该簇的样本集合的误差和
print("sseSplit, and notSplit: ",sseSplit,sseNotSplit)
#两误差和相加即为分簇后整个样本集合的误差和,找出簇中心集合中能让分簇后误差和最小的簇中心,保存最佳簇中心(bestCentToSplit),最佳分簇中心集合(bestNewCents),以及分簇数据集中样本对应簇中心及距离集合(bestClustAss),最小误差(lowestSSE)
if (sseSplit + sseNotSplit) < lowestSSE:
bestCentToSplit = i
bestNewCents = centroidMat
bestClustAss = splitClustAss.copy()
lowestSSE = sseSplit + sseNotSplit
#更新用K-means获取的簇中心集合,将簇中心换为len(centList)和bestCentToSplit,以便之后调整clusterAssment(总样本集对应簇中心与和簇中心距离的矩阵)时一一对应
bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #change 1 to 3,4, or whatever
bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
print('the bestCentToSplit is: ',bestCentToSplit)
print('the len of bestClustAss is: ', len(bestClustAss))
#更新簇中心集合,注意与bestClustAss矩阵是一一对应的
centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids
centList.append(bestNewCents[1,:].tolist()[0])
#reassign new clusters, and SSE
clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss
return mat(centList), clusterAssment二分K值最重要的是记住要将最佳分簇集合与clusterAssment一一对应
测试代码如下:
datMat3 = mat(loadDataSet('testSet2.txt'))
centList,myNewAssments = biKmeans(datMat3,3)
print(centList)
xArr = datMat3[:,0].flatten().A[0]
yArr = datMat3[:,1].flatten().A[0]
xArr1 = centList[:,0].flatten().A[0]
yArr1 = centList[:,1].flatten().A[0]
#paint为笔者自己写的绘图函数
paint(xArr,yArr,xArr1,yArr1)
def paint(xArr,yArr,xArr1,yArr1):
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xArr,yArr,c='blue')
ax.scatter(xArr1,yArr1,c='red')
plt.show()上述函数可以运行多次,聚类会收敛到全局最小值,而原始的别的!!3 ()函数偶尔会陷人局部最小值。
10.4 示例:对地图上的点进行聚类
假如有这样一种情况:你的朋友Drew希望你带他去城里庆祝他的生日。由于其他一些朋友也会过来,所以需要你提供一个大家都可行的计划。Drew给了你一些他希望去的地址。这个地址列表很长,有70个位置。我把这个列表保存在文件portland-Clubs.txt中,该文件和源代码一起打包。这些地址其实都在俄勒冈州的波特兰地区。
也就是说,一晚上要去70个地方!你要决定一个将这些地方进行聚类的最佳策略,这样就可以安排交通工具抵达这些簇的质心,然后步行到每个簇内地址。Drew的清单中虽然给出了地址,但是并没有给出这些地址之间的距离远近信息。因此,你要得到每个地址的纬度和经度,然后对这些地址进行聚类以安排你的行程。
示例:对于地理数据应用二分K-均值算法
(1)收集数据:使用Yahoo!PlaceFinder API收集数据
(2)准备数据:只保留经纬度信息
(3)分析数据:使用Matplotlib来构建一个二维数据图,其中包含簇与地图
(4)训练算法:训练不适用无监督学习
(5)测试算法:使用10.4节中的biKmeans( )函教
(6)使用算法| 最后的输出是包含簇及簇中心的地图
10.4.1 Yahoo! PlaceFinder API
Yahoo! PlaceFinderAPI,代码如下:
import urllib
import json
def geoGrab(stAddress, city):
#create a dict and constants for the goecoder
apiStem = 'http://where.yahooapis.com/geocode?'
#请求参数字典
params = {}
params['flags'] = 'J'#JSON return type
params['appid'] = 'aaa0VN6k'
params['location'] = '%s %s' % (stAddress, city)
#url编码请求参数,化为x1=xx&x2=xx形式
url_params = urllib.urlencode(params)
#print url_params
yahooApi = apiStem + url_params
print(yahooApi)
#请求api
c=urllib.urlopen(yahooApi)
#获取json格式的数据
return json.loads(c.read())
from time import sleep
def massPlaceFind(fileName):
fw = open('places.txt', 'w')
#对文件中的每个样本调用geoGrab()获取json数据,解析后写入源文件
for line in open(fileName).readlines():
line = line.strip()
lineArr = line.split('\t')
retDict = geoGrab(lineArr[1], lineArr[2])
if retDict['ResultSet']['Error'] == 0:
lat = float(retDict['ResultSet']['Results'][0]['latitude'])
lng = float(retDict['ResultSet']['Results'][0]['longitude'])
print("%s\t%f\t%f" % (lineArr[0], lat, lng))
fw.write('%s\t%f\t%f\n' % (line, lat, lng))
else: print("error fetching")
sleep(1)
fw.close()测试代码如下:
geoResults = geoGrab('1 VA Center', 'Augusta, ME')
print(geoResults)由于主要不是为了调用YahooAPI,因此笔者没有实际调用API获取数据,理解这个过程就可以了,首先获取数据,然后调用二分K均值聚类对地址聚类分析。
10.4.2 对地理坐标进行聚类
这个例子中要聚类的俱乐部给出的信息为经度和维度,但这些信息对于距离计算还不够。在北极附近每走几米的经度变化可能达到数10度 ;而在赤道附近走相同的距离,带来的经度变化可能只是零点几。可以使用球面余弦定理来计算两个经纬度之间的距离
球面距离计算及簇绘图函数,代码如下:
#利用球面余弦定理计算指定(经度,纬度)两点的距离
def distSLC(vecA, vecB):#Spherical Law of Cosines
a = sin(vecA[0,1]*pi/180) * sin(vecB[0,1]*pi/180)
b = cos(vecA[0,1]*pi/180) * cos(vecB[0,1]*pi/180) * \
cos(pi * (vecB[0,0]-vecA[0,0]) /180)
return arccos(a + b)*6371.0 #pi is imported with numpy
import matplotlib
import matplotlib.pyplot as plt
def clusterClubs(numClust=5):
datList = []
#读取数据集,存储在datList中
for line in open('places.txt').readlines():
lineArr = line.split('\t')
datList.append([float(lineArr[4]), float(lineArr[3])])
datMat = mat(datList)
#调用二分K聚类获取簇中心集合以及clustAssing矩阵
myCentroids, clustAssing = biKmeans(datMat, numClust, distMeas=distSLC)
fig = plt.figure()
rect=[0.1,0.1,0.8,0.8]
scatterMarkers=['s', 'o', '^', '8', 'p', \
'd', 'v', 'h', '>', '<']
axprops = dict(xticks=[], yticks=[])
ax0=fig.add_axes(rect, label='ax0', **axprops)
imgP = plt.imread('Portland.png')
ax0.imshow(imgP)
ax1=fig.add_axes(rect, label='ax1', frameon=False)
#迭代簇集合,根据不同的marker画出对应的簇
for i in range(numClust):
ptsInCurrCluster = datMat[nonzero(clustAssing[:,0].A==i)[0],:]
markerStyle = scatterMarkers[i % len(scatterMarkers)]
ax1.scatter(ptsInCurrCluster[:,0].flatten().A[0], ptsInCurrCluster[:,1].flatten().A[0], marker=markerStyle, s=90)
#画出所有簇中心
ax1.scatter(myCentroids[:,0].flatten().A[0], myCentroids[:,1].flatten().A[0], marker='+', s=300)
plt.show()测试代码如下:
kMeans.clusterClubs(5)10.5 本章小结
聚类是一种无监督的学习方法。所谓无监督学习是指事先并不知道要寻找的内容,即没有目标变量。聚类将数据点归到多个簇中,其中相似数据点处于同一簇,而不相似数据点处于不同簇中。聚类中可以使用多种不同的方法来计算相似度。
一种广泛使用的聚类算法是K-均值算法,其中K是用户指定的要创建的簇的数目。K-均值聚类算法以K个随机质心开始。算法会计算每个点到质心的距离。每个点会被分配到距其最近的簇质心,然后紧接着基于新分配到簇的点更新簇质心。以上过程重复数次,直到簇质心不再改变。这个简单的算法非常有效但是也容易受到初始簇质心的影响。为了获得更好的聚类效果,可以使用另一种称为二分K-均值的聚类算法。二分K-均值算法首先将所有点作为一个簇,然后使用K-均值算法(K = 2 ) 对其划分。下一次迭代时,选择有最大误差的簇进行划分。该过程重复直到K个簇创建成功为止。二分K-均值的聚类效果要好于K-均值算法。
K-均值算法以及变形的K-均值算法并非仅有的聚类算法, 另外称为层次聚类的方法也被广泛使用