407-Trapping Rain Water II

Description:
Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.

Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.

Example:

Given the following 3x6 height map:
[
  [1,4,3,1,3,2],
  [3,2,1,3,2,4],
  [2,3,3,2,3,1]
]

Return 4.

The above image represents the elevation map [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.

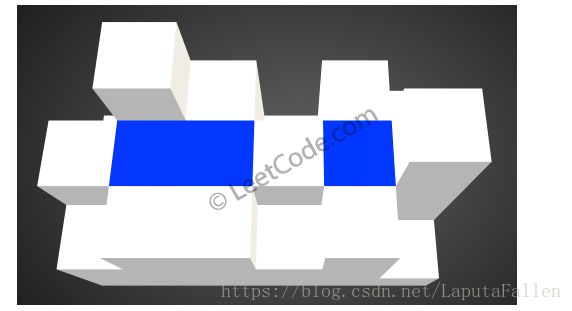
After the rain, water is trapped between the blocks. The total volume of water trapped is 4.

问题描述:
给定一个二维数组，其中每个元素为单位方块(长宽为1)的高度，求下雨后，这个立体空间能盛的水的体积。

例子:
[
[1,4,3,1,3,2],
[3,2,1,3,2,4],
[2,3,3,2,3,1]
]
(1,3)和(1,2)下标的元素变为3,(1,5)变为3，总计为4

关于这个题目，先说一下自己的想法:
如果单纯的想每一个方块如何变化，然后加起来，那完蛋了，比较困难。列一个不太形象的比喻，木桶原理，把整个空间想象为一个整体，除去边缘处(因为雨不可能盛放在边缘，只能从边缘往里流)，每个方块最终的结果为其”观察”周围后能够达到的最大的高度。

有两种解法，都是用的优先级队列。

解法1:

/*
使用优先级队列，优先级判断条件为方块的高度。先把边缘处方块加入优先级队列，优先处理高度最低的。
每取出一个方块，可以看到四个方向的方块，首先排除到已经看过或者行列不满足条件的方块，
如果新方块比当前方块矮，那么最终结果加上两者之差，将新方块的高度改为当前方块高度后加入队列。
如果新方块的高度大于等于当前方块，那么不作处理，将其加入队列。依次处理，直到优先级队列没有元素，
返回最终结果。
*/
class Solution {
    private int[][] dirs = {{0, -1}, {-1, 0}, {0, 1}, {1, 0}};
    //方块类，实现了Comparable接口，用于优先级队列排序
    private class Cell implements Comparable<Cell>{
            int row;
            int col;
            int height;

            public Cell(int row, int col, int height){
                this.row = row;
                this.col = col;
                this.height = height;
            }
            @Override
            public int compareTo(Cell cell1){
                return height - cell1.height;
            }
    }
    public int trapRainWater(int[][] heightMap) {
        if(heightMap == null || heightMap.length == 0 || heightMap[0].length == 0)  return 0;

        int m = heightMap.length, n = heightMap[0].length;
        //由于方块类Cell实现了Comparable，优先级队列不需要定义匿名内部类comparator
        Queue queue = new PriorityQueue();
        boolean[][] visited = new boolean[m][n];

        //首先放入边缘方块
        for(int i = 0;i < m;i++){
            visited[i][0] = true;
            visited[i][n - 1] = true;
            queue.add(new Cell(i, 0, heightMap[i][0]));
            queue.add(new Cell(i, n - 1, heightMap[i][n - 1]));
        }
        for(int j = 1;j < n - 1;j++){
            visited[0][j] = true;
            visited[m - 1][j] = true;
            queue.add(new Cell(0, j, heightMap[0][j]));
            queue.add(new Cell(m - 1, j, heightMap[m - 1][j]));
        }

        int res = 0;
        while(!queue.isEmpty()){
            Cell cell = queue.poll();
            for(int[] dir : dirs){
                int i = cell.row + dir[0], j = cell.col + dir[1];
                //排除不合条件的方块后分情况处理,为了方便，直接使用了两个Math.max()
                if(i >= 0 && i < m && j >= 0 && j < n && !visited[i][j]){
                    visited[i][j] = true;
                    res += Math.max(0, cell.height - heightMap[i][j]);
                    queue.offer(new Cell(i, j, Math.max(heightMap[i][j], cell.height)));
                }
            }
        }

        return res;
    }
}

解法2:

/*
与解法1差异在于加了fill方法。实际上我认为解法2更好理解，可以想象成水面慢慢上升
实际上自习分析解法1，我们也可以看出解法2。如果边缘高度为2,3,4，那么会先处理2，而若2的四个方向
(实际上由于边缘，只有1个方向)中有一个方块高度比它小，那么将其放入优先级队列后会继续处理这个方块，
因为这个方块现在高度变为了2，还是最小的那个，所以实际上是一个递归，于是就有了fill()。直到把
高度为2的连通分量方块处理完它才会结束递归，转回优先级队列
*/
public class Solution {
    private static class Cell implements Comparable {
        private int row;
        private int col;
        private int value;
        public Cell(int r, int c, int v) {
            this.row = r;
            this.col = c;
            this.value = v;
        }
        @Override
        public int compareTo(Cell other) {
            return value - other.value;
        }
    }
    private int water;
    private boolean[][] visited1;
    public int trapRainWater(int[][] heightMap) {
        if (heightMap.length == 0) return 0;
        PriorityQueue walls = new PriorityQueue();
        water = 0;
        visited1 = new boolean[heightMap.length][heightMap[0].length];
        int rows = heightMap.length, cols = heightMap[0].length;
        //build wall;
        for (int c = 0; c < cols; c++) {
            walls.add(new Cell(0, c, heightMap[0][c]));
            walls.add(new Cell(rows - 1, c, heightMap[rows - 1][c]));
            visited1[0][c] = true;
            visited1[rows - 1][c] = true;
        }
        for (int r = 1; r < rows - 1; r++) {
            walls.add(new Cell(r, 0, heightMap[r][0]));
            walls.add(new Cell(r, cols - 1, heightMap[r][cols - 1]));
            visited1[r][0] = true;
            visited1[r][cols - 1] = true;
        }
        //end build wall;
        while(walls.size() > 0) {
            Cell min = walls.poll();
            //变化在这里
            visit(heightMap, min, walls);
        }
        return water;
    }
    private void visit(int[][] height, Cell start, PriorityQueue walls) {
        fill(height, start.row + 1, start.col, walls, start.value);
        fill(height, start.row - 1, start.col, walls, start.value);
        fill(height, start.row, start.col + 1, walls, start.value);
        fill(height, start.row, start.col - 1, walls, start.value);
    }
    //注意fill，是一个递归的函数
    private void fill(int[][] height, int row, int col, PriorityQueue walls, int min) {
        if (row < 0 || col < 0) return;
        else if (row >= height.length || col >= height[0].length) return;
        else if (visited1[row][col]) return;
        else if (height[row][col] >= min) {
            walls.add(new Cell(row, col, height[row][col]));
            visited1[row][col] = true;
            return;
        } else {
            water += min - height[row][col];
            visited1[row][col] = true;
            fill(height, row + 1, col, walls, min);
            fill(height, row - 1, col, walls, min);
            fill(height, row, col + 1, walls, min);
            fill(height, row, col - 1, walls, min);
        }
    }
}