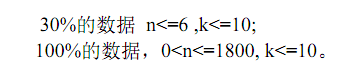计数【NOIP2016提高A组模拟7.15】

题目

样例输入：

2 10
样例输出：

90

数据范围:

---

剖解题目：题目说的很明了了。

---

思路:求方案数，一般会设计道dp，规律之类的。

---

解法：数位DP，设f[i][j]表示当前到了第i位，这一位的数字是j的方案数。
自然有：f[i][j]=f[i-1][l]+f[i][j]。(0<=l < k)且（l<>0 and j<>0）.
看到这位数，很明显的高精度了。
然而单纯的高精加速度会较慢，我们惊讶发现其实只有f[i][0]与f[i][!0]是不同的，所以我们可以将所有的f[i][!0]都加在一起，也就是弄一个高精乘。
然而，高精度实在是难搞，调了半天终于调对了，真是蛋疼！(ノಠ益ಠ)ノ彡┻━┻

---

代码：

type
        arr=array[0..1,0..1,0..2000]of longint;
const mo=100000000;
var
        f:arr;
        ans:array[0..1000]of longint;
        n,k,i,j,x,y,z,p,q:longint;
procedure
        add(x,y,xx,yy:longint);
var
        i,t:longint;
begin
        if f[x,xx,0]>f[y,yy,0] then i:=f[x,xx,0]
        else i:=f[y,yy,0];
        t:=0;
        for i:=1 to i do
        begin
                if i>f[x,xx,0] then f[x,xx,i]:=0;
                if i>f[y,yy,0] then f[y,yy,i]:=0;
                f[x,xx,i]:=f[x,xx,i]+f[y,yy,i]+t;
                t:=f[x,xx,i] div mo;
                f[x,xx,i]:=f[x,xx,i] mod mo;
        end;
        if t>0 then
        begin
                inc(i);
                f[x,xx,i]:=t;
        end;
        f[x,xx,0]:=i;
end;
procedure
        quick(x,o,k:longint);
var
        i,t:longint;
begin
        i:=f[x,o,0];
        t:=0;
        for i:=1 to i do
        begin
                f[x,o,i]:=f[x,o,i]*k+t;
                t:=f[x,o,i] div mo;
                f[x,o,i]:=f[x,o,i] mod mo;
        end;
        while t<>0 do
        begin
                inc(i);
                f[x,o,i]:=f[x,o,i]+t;
                t:=f[x,o,i] div mo;
        end;
        f[x,o,0]:=i;
end;
procedure
        printf(x:longint);
var
        i:longint;
        s:string;
begin
        write(f[x,1,f[x,1,0]]);
        for i:=f[x,1,0]-1 downto 1 do
        begin
                f[x,1,i]:=f[x,1,i]+mo;
                str(f[x,1,i],s);
                delete(s,1,1);
                write(s);
        end;
end;
begin
        readln(n,k);
        if k=1 then writeln(0)
        else if n=1 then writeln(k-1)
        else begin
                f[0,0,0]:=1;
                f[0,0,1]:=1;
                f[0,1,0]:=1;
                f[0,1,1]:=1;
                p:=1; q:=0;
                for i:=2 to n do
                begin
                        quick(q,1,k-1);
                        f[p,0]:=f[q,1];
                        f[p,1]:=f[q,1];
                        add(p,q,1,0);
                        q:=p;
                        p:=p xor 1;
                end;
                quick(q,1,k-1);
                printf(q);

        end;
end.