支持向量机（SVM）的SMO算法实现（Python）

最近在学支持向量机，总感觉对SMO理解的不够透彻，就编写程序来检验自己的理解

完全参照John C. Platt《Sequential Minimal Optimization - A Fast Algorithm for Training Support Vector Machines》中的伪代码编写的Python程序（去除了文中的tol）

参考（感谢前辈们^_^）：

支持向量机通俗导论（理解SVM的三层境界）

支持向量机（五）SMO算法 

Python实现SVM(支持向量机)（数据引用）

代码：

#SVM-SMO
#by ald

import numpy as np
import matplotlib.pyplot as plt

def load_data_set(fileName):
    data_sets = []
    label_sets = []
    with open(fileName) as fr:
        for line in fr.readlines():
            lineArr = line.strip().split('\t') #去除两边空白符，按制表符分割
            data_sets.append([float(lineArr[0]), float(lineArr[1])])
            label_sets.append(float(lineArr[2]))
    data_sets = np.array(data_sets)
    label_sets = np.array([label_sets]).T
    return data_sets, label_sets

class OptStruct:
    def __init__(self, point, target, C): # point array格式的样本集， target array格式的标签集
        self.point = point
        self.target = target
        self.C = C
        self.m = np.shape(point)[0] #样本数量
        self.alphas = np.zeros((self.m, 1))
        self.b = 0
        self.e_cache = np.zeros((self.m, 2)) #储存E
        self.Gamma = np.dot(point, point.T)

def cal_Ei(i, opt_struct1):
    f_point_i = float(np.dot((opt_struct1.target * opt_struct1.alphas).T, opt_struct1.Gamma[i].T)) + opt_struct1.b
    Ei = f_point_i - opt_struct1.target[i]
    return Ei

def select_i1_heuristic(i2, opt_struct1, E2):
    valid_e_cache = np.nonzero(opt_struct1.e_cache[:, 0])[0]
    max_delta_E = np.argmax(np.fabs(opt_struct1.e_cache[valid_e_cache, 1] - E2))
    i1 = valid_e_cache[max_delta_E]
    return i1

def take_step(i1, i2, opt_struct1):
    if i1 == i2:
        return False
    global y2, alpha2, E2, eps
    alpha1 = opt_struct1.alphas[i1]
    y1 = opt_struct1.target[i1]
    E1 = cal_Ei(i1, opt_struct1)
    opt_struct1.e_cache[i1] = [1, E1] #chech in error cache
    s = y1 * y2
    if y1 == y2:
        L = max(0, alpha2 + alpha1 - C)
        H = min(C, alpha2 + alpha1)
    else:
        L = max(0, alpha2 - alpha1)
        H = min(C, C + alpha2 + alpha1)
    if L == H:
        return False
    k11 = np.dot(opt_struct1.point[i1], opt_struct1.point[i1].T)
    k12 = np.dot(opt_struct1.point[i1], opt_struct1.point[i2].T)
    k22 = np.dot(opt_struct1.point[i2], opt_struct1.point[i2].T)
    eta = k11 + k22 - 2 * k12
    if eta > 0:
        a2 = alpha2 + y2 * (E1 - E2) / eta
        if a2 < L:
            a2 = L
        elif a2 > H:
            a2 = H
    else:
        f1 = y1 * (E1 + opt_struct1.b) - alpha1 * k11 - s * alpha2 * k22
        f2 = y2 * (E2 + opt_struct1.b) - s * alpha1 * k12 - alpha2 * k22
        L1 = alpha1 + s * (alpha2 - L)
        H1 = alpha1 + s * (alpha2 - H)
        L_obj = L1 * f1 + L * f2 + 0.5 * L1 * L1 * k11 + 0.5 * L * L * k22 + s * L * L1 * k12
        H_obj = H1 * f1 + H * f2 + 0.5 * H1 * H1 * k11 + 0.5 * H * H * k22 + s * H * H1 * k12
        if L_obj < H_obj - eps:
            a2 = L
        elif L_obj > H_obj + eps:
            a2 = H
        else:
            a2 = alpha2
    if abs(a2 - alpha2) < eps * (a2 + alpha2 + eps):
        return False
    a1 = alpha1 + s * (alpha2  - a2)
    b1 = -E1 - y1 * (a1 - alpha1) * k11 + y2 * (a2 - alpha2) * k12 + opt_struct1.b
    b2 = -E2 - y1 * (a1 - alpha1) * k12 + y2 * (a2 - alpha2) * k22 + opt_struct1.b
    if 0 < a1  1 and alpha2 > 0): #如果违反KKT条件，选择i1,如果发生更新，返回1
        if np.sum((opt_struct1.alphas != 0) * (opt_struct1.alphas != C)) > 1: #如果非界样本数量>1
            i1 = select_i1_heuristic(i2, opt_struct1, E2) #启发式方法从非界样本中选择i1
            if take_step(i1, i2, opt_struct1 = opt_struct1):
                return 1
        #如果启发式方法找到的i1不可行，遍历非界样本集寻找可行的i1（随机开始）
        non_bound_alphas = np.nonzero((opt_struct1.alphas != 0) * (opt_struct1.alphas != C))[0] #局部变量
        np.random.shuffle(non_bound_alphas) #随机打乱
        for k in non_bound_alphas:
            if take_step(k, i2, opt_struct1):
                return 1
        #如果仍没有找到可行的i1,遍历边界样本集寻找i1
        bound_alphas = np.nonzero((opt_struct1.alphas == 0) + (opt_struct1.alphas == C))[0]
        np.random.shuffle(bound_alphas)
        for j in bound_alphas:
            if take_step(j, i2, opt_struct1):
                return 1
    return 0 #不违反KKT条件，返回0

def plot_result(point_sets, target_sets, w, b):
    x1_positive = []
    x2_positive = []
    x1_negeitve = []
    x2_negetive = []
    for i in range(len(target_sets)):
        if int(target_sets[i]) == 1:
            x1_positive.append(point_sets[i, 0])
            x2_positive.append(point_sets[i, 1])
        else:
            x1_negeitve.append(point_sets[i, 0])
            x2_negetive.append(point_sets[i, 1])
    x = np.linspace(2, 8)
    y = (-b - w[0] * x) / w[1]
    plt.plot(x1_positive, x2_positive, 'o')
    plt.plot(x1_negeitve, x2_negetive, 's')
    plt.plot(x, y)

point_sets, target_sets = load_data_set('testSet.txt')
opt_struct1 = OptStruct(point_sets, target_sets, 1)
C = 1000
iters = 0 #迭代次数
num_changed = 0 #更新计数
examine_all = True #是否循环所有样本
eps = 0.00001 #允许误差，原文献中取0.001
max_iters = 500

while iters <= max_iters and num_changed > 0 or examine_all:
    num_changed = 0
    if examine_all:
        for i in range(0, opt_struct1.m):
            num_changed += examine_example(i, opt_struct1) #检查所有样本
    else:
        #检查 0 < alpha < C 的样本（非界样本）
        non_bound_alphas = np.nonzero((opt_struct1.alphas != 0) * (opt_struct1.alphas != C))[0]
        for i in non_bound_alphas:
            num_changed += examine_example(i, opt_struct1)
    iters += 1
    #如果检查了所有样本，下次就只检查非界样本，
    #如果非界样本全部合法，下次就要检查全部的样本
    if examine_all:
        examine_all = False
    elif num_changed == 0:
        examine_all = True

w = np.dot((target_sets * opt_struct1.alphas).T, point_sets).flatten()
print()
print('w:', w)
print('b:', opt_struct1.b)
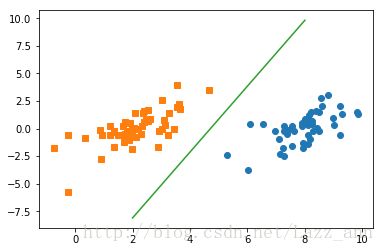
plot_result(point_sets, target_sets, w, opt_struct1.b)

结果：