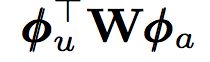UCB算法升职记——LinUCB算法
UCB再回顾
上回书说到,UCB这个小伙子在做EE(Exploit-Explore)的时候表现不错,只可惜啊,是一个不关心组织的上下文无关(context free)bandit算法,它只管埋头干活,根本不观察一下面对的都是些什么样的arm。
进一步送UCB去深造之前,我们再把UCB算法要解决的问题描述一下:
面对固定的K个item(广告或推荐物品),我们没有任何先验知识,每一个item的回报情况完全不知道,每一次试验要选择其中一个,如何在这个选择过程中最大化我们的回报?
UCB解决这个Multi-armed bandit问题的思路是:用置信区间。置信区间可以简单地理解为不确定性的程度,区间越宽,越不确定,反之亦反之。
每个item的回报均值都有个置信区间,随着试验次数增加,置信区间会变窄(逐渐确定了到底回报丰厚还是可怜)。
每次选择前,都根据已经试验的结果重新估计每个item的均值及置信区间。
选择置信区间上限最大的那个item。
“选择置信区间上界最大的那个item”这句话反映了几个意思:
- 如果item置信区间很宽(被选次数很少,还不确定),那么它会倾向于被多次选择,这个是算法冒风险的部分;
- 如果item置信区间很窄(备选次数很多,比较确定其好坏了),那么均值大的倾向于被多次选择,这个是算法保守稳妥的部分;
- UCB是一种乐观的算法,选择置信区间上界排序,如果时悲观保守的做法,是选择置信区间下界排序。
给UCB插上特征的翅膀
UCB还是很有前途的,所以算法大神们还是有心提携它一把。
这不,Yahoo!的科学家们在2010年发表了一篇论文[1],给UCB指了一条明路,同时还把改造后的UCB算法用在了Yahoo!的新闻推荐中,深造后的UCB算法现在title叫LinUCB。
这篇论文很有名,很多地方都有引用,在刘鹏博士的著作《计算广告》中也专门讲到了[2]。我知道,大家都很忙,尤其是面对英文论文,尤其是论文中有大量的数学公式,所以“没时间”去阅读它,所以这里我就转述一下这个算法的改造过程,以期望大家在百忙之中能够领会其精神。
单纯的老虎机,它回报情况就是老虎机自己内部决定的,而在广告推荐领域,一个选择的回报,是由User和Item一起决定的,如果我们能用feature来刻画User和Item这一对CP,在选择之前通过feature预估每一个arm的期望回报及置信区间,那就合理多了。
为UCB插上特征的翅膀,这就是LinUCB最大的特色。
LinUCB算法做了一个假设:一个Item被选择后推送给一个User,其回报和相关Feature成线性关系,这里的“相关feature”就是context,也是实际项目中发挥空间最大的部分。
于是试验过程就变成:用User和Item的特征预估回报及其置信区间,选择置信区间上界最大的item推荐,观察回报后更新线性关系的参数,以此达到试验学习的目的。
LinUCB基本算法描述如下:
对照每一行解释一下:
0. 设定一个参数\alpha,这个参数决定了我们Explore的程度
1. 开始试验迭代
2. 获取每一个arm的特征向量xa,t
3. 开始计算每一个arm的预估回报及其置信区间
4. 如果arm还从没有被试验过,那么:
5. 用单位矩阵初始化Aa
6. 用0向量初始化ba,
7. 处理完没被试验过的arm
8. 计算线性参数\theta
9. 用\theta和特征向量xa,t计算预估回报, 同时加上置信区间宽度
10. 处理完每一个arm
11. 选择第9步中最大值对应的arm,观察真实的回报rt
12. 更新Aat
13. 更新bat
14. 算法结束
本来,按照上面的步骤已经可以写代码完成KPI了,但是我们都是爱学习的小伙伴,其中一些关键的地方还得弄得更明白些。
注意到上面的第4步,给特征矩阵加了一个单位矩阵,这就是岭回归(ridge regression),岭回归主要用于当样本数小于特征数时,对回归参数进行修正[3]。
对于加了特征的bandit问题,正符合这个特点:试验次数(样本)少于特征数。
每一次观察真实回报之后,要更新的不止是岭回归参数,还有每个arm的回报向量ba。
实现LinUCB
根据论文给出的算法描述,其实很好写出LinUCB的代码[5],麻烦的只是构建特征。
代码如下,一些必要的注释说明已经写在代码中。
class LinUCB:
def __init__(self):
self.alpha = 0.25
self.r1 = 1 # if worse -> 0.7, 0.8
self.r0 = 0 # if worse, -19, -21
# dimension of user features = d
self.d = 6
# Aa : collection of matrix to compute disjoint part for each article a, d*d
self.Aa = {}
# AaI : store the inverse of all Aa matrix
self.AaI = {}
# ba : collection of vectors to compute disjoin part, d*1
self.ba = {}
self.a_max = 0
self.theta = {}
self.x = None
self.xT = None
# linUCB
def set_articles(self, art):
# init collection of matrix/vector Aa, Ba, ba
for key in art:
self.Aa[key] = np.identity(self.d)
self.ba[key] = np.zeros((self.d, 1))
self.AaI[key] = np.identity(self.d)
self.theta[key] = np.zeros((self.d, 1))
"""
这里更新参数时没有传入更新哪个arm,因为在上一次recommend的时候缓存了被选的那个arm,所以此处不用传入
另外,update操作不用阻塞recommend,可以异步执行
"""
def update(self, reward):
if reward == -1:
pass
elif reward == 1 or reward == 0:
if reward == 1:
r = self.r1
else:
r = self.r0
self.Aa[self.a_max] += np.dot(self.x, self.xT)
self.ba[self.a_max] += r * self.x
self.AaI[self.a_max] = linalg.solve(self.Aa[self.a_max], np.identity(self.d))
self.theta[self.a_max] = np.dot(self.AaI[self.a_max], self.ba[self.a_max])
else:
# error
pass
"""
预估每个arm的回报期望及置信区间
"""
def recommend(self, timestamp, user_features, articles):
xaT = np.array([user_features])
xa = np.transpose(xaT)
art_max = -1
old_pa = 0
# 获取在update阶段已经更新过的AaI(求逆结果)
AaI_tmp = np.array([self.AaI[article] for article in articles])
theta_tmp = np.array([self.theta[article] for article in articles])
art_max = articles[np.argmax(np.dot(xaT, theta_tmp) + self.alpha * np.sqrt(np.dot(np.dot(xaT, AaI_tmp), xa)))]
# 缓存选择结果,用于update
self.x = xa
self.xT = xaT
# article index with largest UCB
self.a_max = art_max
return self.a_max
怎么构建特征
LinUCB算法有一个很重要的步骤,就是给User和Item构建特征,也就是刻画context。在原始论文里,Item是文章,其中专门介绍了它们怎么构建特征的,也甚是精妙。容我慢慢表来。
- 原始用户特征有:
人口统计学:性别特征(2类),年龄特征(离散成10个区间)
地域信息:遍布全球的大都市,美国各个州
行为类别:代表用户历史行为的1000个类别取值
- 原始文章特征:
URL类别:根据文章来源分成了几十个类别
编辑打标签:编辑人工给内容从几十个话题标签中挑选出来的
原始特征向量都要归一化成单位向量。
还要对原始特征降维,以及模型要能刻画一些非线性的关系。
用Logistic Regression去拟合用户对文章的点击历史,其中的线性回归部分为:
拟合得到参数矩阵W,可以将原始用户特征(1000多维)投射到文章的原始特征空间(80多维),投射计算方式:
这是第一次降维,把原始1000多维降到80多维。
然后,用投射后的80多维特征对用户聚类,得到5个类簇,文章页同样聚类成5个簇,再加上常数1,用户和文章各自被表示成6维向量。
Yahoo!的科学家们之所以选定为6维,因为数据表明它的效果最好[4],并且这大大降低了计算复杂度和存储空间。
我们实际上可以考虑三类特征:U(用户),A(广告或文章),C(所在页面的一些信息)。
前面说了,特征构建很有发挥空间,算法工程师们尽情去挥洒汗水吧。
总结
总结一下LinUCB算法,有以下优点:
- 由于加入了特征,所以收敛比UCB更快(论文有证明);
- 特征构建是效果的关键,也是工程上最麻烦和值的发挥的地方;
- 由于参与计算的是特征,所以可以处理动态的推荐候选池,编辑可以增删文章;
- 特征降维很有必要,关系到计算效率。
另外,可能有人已经发现了,bandit算法有个问题,就是要求同时参与候选的arm数量不能太多,几百上千个差不多了,更多就不好处理了,如果arm更多的时候,recommend也是异步计算,这块可以深思一下,尽是工程上的事。
当年在学习Yahoo!这篇介绍LinUCB论文时,还一一看了其参考文献,比如这两篇,一个是关于特征处理的[6],一个是关于降维和数据分析的[7],有兴趣也可以看看,这里就不画重点了,高考不考。
[1] http://www.research.rutgers.edu/~lihong/pub/Li10Contextual.pdf
[2] 《计算广告:互联网商业变现的市场与技术》p253, 刘鹏,王超著
[3] https://en.wikipedia.org/wiki/Tikhonov_regularization
[4] http://www.gatsby.ucl.ac.uk/~chuwei/paper/isp781-chu.pdf
[5] https://github.com/Fengrui/HybridLinUCB-python/blob/master/policy_hybrid.py
[6] http://www.wwwconference.org/www2009/proceedings/pdf/p691.pdf
[7] http://www.gatsby.ucl.ac.uk/~chuwei/paper/isp781-chu.pdf