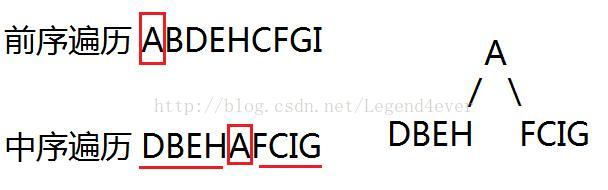CAIOJ1034 二叉树的后序遍历(经典递归)
http://caioj.cn/problem.php?id=1034
这题就是已知一棵二叉树的前序遍历和中序遍历,求这棵树的后序遍历,也就是传说中裸题。
做这题之前先要了解二叉树到底是什么,这里就不作赘述,直接搬上度娘的链接 二叉树-百度百科
二叉树的遍历分3种,没错就是题中的前序遍历(也叫做先序遍历),中序遍历,后序遍历。
前序遍历遵循的规则是:根左右(就是我有根就优先输出根,没根就优先输出左儿子,没左儿子就优先输出右儿子)
中序遍历遵循的规则是:左根右(优先找到最底层的左儿子输出,没左儿子就优先输出根,最后才轮到捡回来的右儿子(雾))
后序遍历遵循的规则是:左右根(相信也不用多说了,这次捡回来的不是儿子是我们的根(最低优先级))
不熟悉的同学可以先自己在纸上随意画出二叉树,然后根据前中后序遍历的规则自己多写几遍,就能逐渐熟悉。
根据个人总结,中序遍历就好像我们把整棵树压扁到一行,从左到右写出来一样(手写的时候可以参考这个思路,但是计算机逻辑的话就是另一回事了。。。)
好的,现在我们已经了解了二叉树的前中后序遍历的规则了,那么知道一棵树的前序遍历和中序遍历,我们怎么才能求出一棵树的后序遍历呢?
如图,在前序遍历中,根据它的规则我们可以得知,在当前这一步,前序遍历中的第一个字母肯定就是这棵树的根,
所以我们把A取出来,中序遍历中肯定也会有A节点的信息,所以我们就在中序遍历中,找到前序遍历中第一个节点字母相对应字母的位置在哪里,
此时,根据中序遍历的规则我们可以知道,
我们假象一下这棵树,执行完这两步后,DBEH这4个节点是不是肯定是在A节点的左边? FCIG这4个节点是不是肯定是A节点的右边?
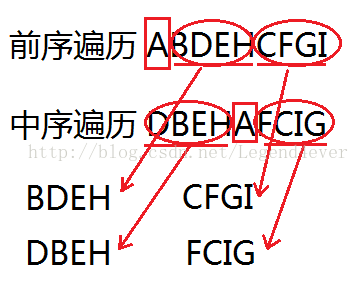
这个时候,我们就以A为截断点,将中序遍历切成了2段,分别为A节点的左子树部分和右子树部分,很明显,中序遍历现在变成了两棵独立的数,
我们只需要分别对这两棵树进行相同的操作就可以继续往下递推了。
下面贴代码:
#include
#include
#include
#define f(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
char qx[110],zx[110],ans[110];
int lenq,lenz,set[110],LEN;
void dfs(int ql,int qr,int zl,int zr)
{
int lnum;
if(ql>qr)
return;
lnum=set[qx[ql]]-zl; //前序遍历中的第一个节点x(即当前根节点),在中序遍历中的位置,
//减去中序遍历当前第一个节点的位置,即求x左边有多少个节点。
dfs(ql+1,ql+lnum,zl,set[qx[ql]]-1);
dfs(ql+lnum+1,qr,set[qx[ql]]+1,zr);
LEN++;
ans[LEN]=qx[ql];
}
int main()
{
scanf("%s",zx+1);
scanf("%s",qx+1);
lenq=strlen(qx+1);
lenz=strlen(zx+1);
f(i,1,lenz)
set[zx[i]]=i;
LEN=0;
dfs(1,lenq,1,lenz);
f(i,1,LEN)
printf("%c",ans[i]);
printf("\n");
return 0;
}