torch学习

torch是一个基于LuaJIT的科学计算框架。
详情见 http://torch.ch/

安装torch

参考http://torch.ch/docs/getting-started.html
在terminal中输入以下命令即可：

git clone https://github.com/torch/distro.git ~/torch --recursive
cd ~/torch; bash install-deps;
./install.sh

其中install-deps用于安装LuaJIT和Torch所需的依赖包，而install.sh用于安装LuaJIT和LuaRocks并用LuaRocks安装torch。

运行torch

在terminal中输入th即可。
运行文件输入dofile "file.lua"即可。
在terminal中运行lua文件则输入

th file.lua

使用torch例子

网站提供很多相关例子在Cheatsheet中：https://github.com/torch/torch7/wiki/Cheatsheet
下面是一个使用导数和梯度下降求二次函数最小值的例子，参考http://torch.ch/docs/five-simple-examples.html

定义一个正定二次型

require 'torch'

torch.manualSeed(1234)

N = 5

-- 创建一个随机的N x N矩阵A
A = torch.rand(N, N)

-- 把A变成对称
A = A*A:t()

-- 把A变成正定
A:add(0.001, torch.eye(N))

-- 创建一个随机向量b
b = torch.rand(N)

-- 创建一个二次型函数
function J(x)
    return 0.5*x:dot(A*x)-b:dot(x)
end

-- 输出某一随机点的函数值
print(J(torch.rand(N)))

输出该二次型函数的最小值

显然该二次型函数在 x∗=A−1b 处取得最小值

xs = torch.inverse(A)*b
print(string.format('J(x^*) = %g', J(xs)))

样例输出：

J(x^*) = -3.13684

使用梯度下降来求最小值

-- J(x)的梯度
function dJ(x)
    return A*x-b
end

x = torch.rand(N)
lr = 0.01
for i=1,20000 do
    x = x - dJ(x)*lr
    -- 输出每次迭代的目标函数值
    print(string.format('at iter %d J(x) = %f', i, J(x)))
end

样例输出：

...
at iter 19995 J(x) = -3.135664
at iter 19996 J(x) = -3.135664
at iter 19997 J(x) = -3.135665
at iter 19998 J(x) = -3.135665
at iter 19999 J(x) = -3.135665
at iter 20000 J(x) = -3.135666

使用optim包

默认已经安装了optim包，如果没安装，可以使用luarocks install optim安装。

do
    local neval = 0
    function JdJ(x)
        local Jx = J(x)
        neval = neval + 1
        print(string.format('after %d evaluations J(x) = %f', neval, Jx))
        return Jx, dJ(x)
    end
end

require 'optim'

state = {
   verbose = true,
   maxIter = 100
}

x = torch.rand(N)
optim.cg(JdJ, x, state)

样例输出：

...
after 120 evaluation J(x) = -3.136835
after 121 evaluation J(x) = -3.136836
after 122 evaluation J(x) = -3.136837
after 123 evaluation J(x) = -3.136838
after 124 evaluation J(x) = -3.136840
after 125 evaluation J(x) = -3.136838

可视化图表

可视化图表需要使用gnuplot包，同理默认已安装。可使用luarocks install gnuplot安装。

evaluations = {}
time = {}
timer = torch.Timer()
neval = 0
function JdJ(x)
    local Jx = J(x)
    neval = neval + 1
    print(string.format('after %d evaluations, J(x) = %f', neval, Jx))
    table.insert(evaluations, Jx)
    table.insert(time, timer:time().real)
    return Jx, dJ(x)
end


-- 使用梯度下降求最小值
state = {
    verbose = true,
    maxIter = 100
}

x0 = torch.rand(N)
cgx = x0:clone()
timer:reset()
optim.cg(JdJ, cgx, state)

-- 保存时间和值
cgtime = torch.Tensor(time)
cgevaluations = torch.Tensor(evaluations)


-- 使用随机梯度下降求最小值
evaluations = {}
time = {}
neval = 0
state = {
    lr = 0.1
}

-- 使用同样的初始值
x = x0:clone()

timer:reset()

for i=1,1000 do
    optim.sgd(JdJ, x, state)
    table.insert(evaluations, Jx)
end

sgdtime = torch.Tensor(time)
sgdevaluations = torch.Tensor(evaluations)


-- 输出可视化图表到plot.png
require 'gnuplot'
gnuplot.pngfigure('plot.png')
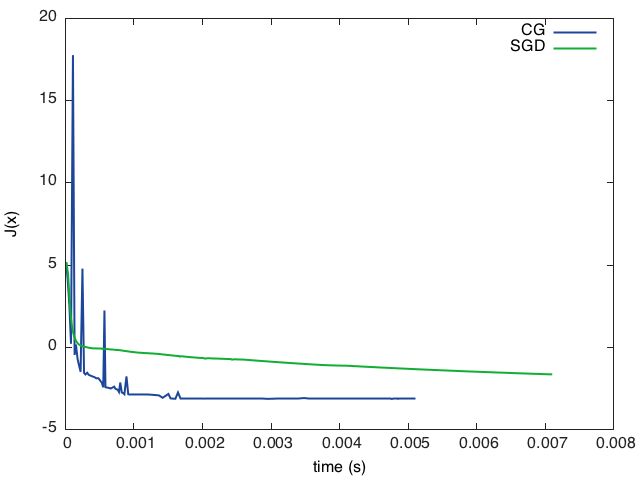
gnuplot.plot(
   {'CG',  cgtime,  cgevaluations,  '-'},
   {'SGD', sgdtime, sgdevaluations, '-'})
gnuplot.xlabel('time (s)')
gnuplot.ylabel('J(x)')
gnuplot.plotflush()

输出图像大致如下