关联规则挖掘（二）-- Apriori 算法

本文首先介绍了Apriori算法的原理，进行了简单的示例推导，而后运用R语言中的arules包对Groceries数据集进行关联规则挖掘实战。

一、概述

Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法，这种算法所针对的关联规则是单维、单层、布尔关联规则。
在前一篇文章中写到关联规则挖掘算法的总体性能取决于寻找频繁项集，而后由频繁项集产生强关联规则就很容易了。那么如何寻找频繁项集呢？自然的想法是对于数据集D，遍历它的每一条记录T，得到T的所有子集，然后计算每一个子集的支持度，最后的结果再与最小支持度比较。此种方法的计算量非常巨大，显然是不可取的。因此，Apriori算法提出了逐层搜索的迭代方法：
1.自连接获取候选集。第一轮的候选集就是数据集D中的项，而其他轮次的候选集则是由前一轮次频繁集自连接得到（频繁集由候选集剪枝得到）。
2.对候选集进行剪枝。剪枝规则1：如果某条候选集的支持度小于最小支持度，那么就会被剪掉；剪枝规则2：如果某条候选集的子集中存在非频繁集，该候选集也会被剪掉。
值得注意的是，为了提高频繁项集逐层产生的效率，进一步减少计算量，一种称作 Apriori 性质的重要性质被用于压缩搜索空间，即：频繁项集的所有非空子集都必须也是频繁的（对应剪枝规则2）。

二、示例推导

该示例基于某事务数据库，数据库中有9个事务，如下图所示：

如何使用Apriori算法寻找频繁项集呢？具体如下：
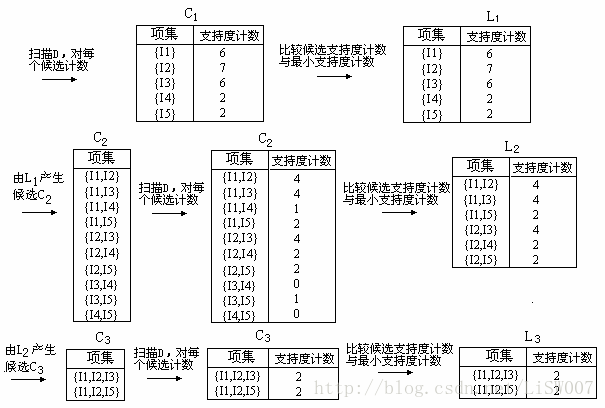
1.在算法的第一次迭代，每个项都是候选 1-项集的集合 C1 的成员。算法简单地扫描所有的事务，对每个项的出现次数计数。
2.假定最小事务支持计数为 2（即，min_sup = 2/9 = 22%）。可以确定频繁 1-项集的集合 L1 。它由具有最小支持度的候选 1-项集组成。
3.为发现频繁 2-项集的集合 L2 ，算法使用 L1 与 L1 自连接产生候选 2-项集的集合 C2 。
4.下一步，扫描 D 中事务，计算 C2 中每个候选项集的支持计数，如下图的第二行的中间表所示。
5.将候选集支持度计数与最小支持度比较，产生频繁 2-项集的集合 L2 。
6.产生候选 3-项集的集合 C3 。首先， L2 与 L2 自连接得到 {I1,I2,I3},{I1,I2,I5},{I1,I3,I5},{I2,I3,I4},{I2,I3,I5},{I2,I4,I5} 。根据Apriori 性质，频繁项集的所有子集必须是频繁的，我们可以确定后 4 个候选不可能是频繁的。因此，我们把它们由 C3 删除，这样，在此后扫描 D 确定 L3 时就不必再求它们的计数值。值得注意的是，Apriori 算法使用逐层搜索技术，给定 k-项集，我们只需要检查它们的(k-1)-子集是否频繁。
7.扫描 D 中事务，以确定 L3 ，它由具有最小支持度的 C3 中的候选 3-项集组成。
8.产生候选 4-项集的集合 C4 。 L3 与 L3 自连接得到 {I1,I2,I3,I5} ，由于其子集 {I1,I3,I5} 不是频繁的，所以 C4 为空，算法终止。

三、实例

1.R语言函数介绍

R语言中arules包可以实现Apriori算法。

• apriori 函数的用法：

apriori(data,parameter=list(support=0.1,confidence=0.8,minlen=1,maxlen=10))
其中parameter参数是一个列表，包含支持度，置信度，和minlen，maxlen即规则包含的元素个数（LHS+RHS），默认的minlen = 1，意味着 {}=>beer 是合法的规则，我们往往不需要这种规则，所以一般设定minlen = 2。

2.R语言实战

本次实战采用arules包中的数据集Groceries，该数据集来自现实生活中某超市的一个月经营数据。

（1）了解数据集

> #下载并加载包
> install.packages("arules")
> library("arules")
> #调用数据集，并查看summary
> data(Groceries)
> summary(Groceries)
transactions as itemMatrix in sparse format with
 9835 rows (elements/itemsets/transactions) and
 169 columns (items) and a density of 0.02609146 

most frequent items:
      whole milk other vegetables       rolls/buns             soda           yogurt 
            2513             1903             1809             1715             1372 
         (Other) 
           34055 

element (itemset/transaction) length distribution:
sizes
   1    2    3    4    5    6    7    8    9   10   11   12   13   14   15   16   17 
2159 1643 1299 1005  855  645  545  438  350  246  182  117   78   77   55   46   29 
  18   19   20   21   22   23   24   26   27   28   29   32 
  14   14    9   11    4    6    1    1    1    1    3    1 

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  1.000   2.000   3.000   4.409   6.000  32.000 

includes extended item information - examples:
       labels  level2           level1
1 frankfurter sausage meat and sausage
2     sausage sausage meat and sausage
3  liver loaf sausage meat and sausage

summary(Groceries)的解释：
第一段：该数据集9835条交易记录，169种交易商品，稀疏矩阵的密度为0.02609146，即所有购物篮的商品总数量为9835*169*0.02609146=43367。
第二段：出现频率最高的商品为whole milk：2513次，other vegetables：1903次等。
第三段：购物篮里商品数量，其中只买了一件商品的订单有2159个，购物篮里商品最多的有32件商品。
第四段：购物篮里商品的五数总括和平均数。
第五段：数据集除了商品名称，还包括其他信息，在这里是商品所属类别level2和level1，level2是小类，level1是大类。

> #进一步查看数据集信息
> inspect(Groceries[1:5])
    items                     
[1] {citrus fruit,            
     semi-finished bread,     
     margarine,               
     ready soups}             
[2] {tropical fruit,          
     yogurt,                  
     coffee}                  
[3] {whole milk}              
[4] {pip fruit,               
     yogurt,                  
     cream cheese ,           
     meat spreads}            
[5] {other vegetables,        
     whole milk,              
     condensed milk,          
     long life bakery product}
> basketsize <- size(Groceries)
> itemfreq <- itemFrequency(Groceries)

解释：
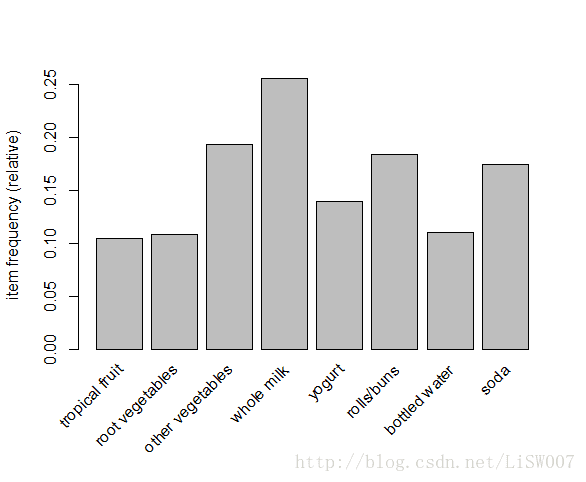
size函数和itemFrequency函数都是arules包中的函数，前者是为了计算购物篮里商品数量，后者是为了计算每种商品的支持度。而itemFrequencyPlot则可以画出条形图进行展现，如下：

> itemFrequencyPlot(Groceries, support = 0.1)

> itemFrequencyPlot(Groceries, topN = 10)

（2）关联规则挖掘

为了进行关联规则挖掘，第一步要根据具体的业务知识设定最小支持度。根据日订单9835/30=328，时订单328/12=27，可知该超市为一个中型超市，我们假设最小支持度为某商品每天至少被购买两次即2*30/9835=0.006。最小置信度暂定为0.25。

> #提取关联规则
> rules <- apriori(Groceries,parameter = list(support = 0.006, confidence = 0.25, minlen = 2))
Apriori

Parameter specification:
 confidence minval smax arem  aval originalSupport maxtime support minlen maxlen target
       0.25    0.1    1 none FALSE            TRUE       5   0.006      2     10  rules
   ext
 FALSE

Algorithmic control:
 filter tree heap memopt load sort verbose
    0.1 TRUE TRUE  FALSE TRUE    2    TRUE

Absolute minimum support count: 59 

set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[169 item(s), 9835 transaction(s)] done [0.00s].
sorting and recoding items ... [109 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 2 3 4 done [0.00s].
writing ... [463 rule(s)] done [0.00s].
creating S4 object  ... done [0.00s].
> summary(rules)
set of 463 rules

rule length distribution (lhs + rhs):sizes
  2   3   4 
150 297  16 

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  2.000   2.000   3.000   2.711   3.000   4.000 

summary of quality measures:
    support           confidence          lift            count      
 Min.   :0.006101   Min.   :0.2500   Min.   :0.9932   Min.   : 60.0  
 1st Qu.:0.007117   1st Qu.:0.2971   1st Qu.:1.6229   1st Qu.: 70.0  
 Median :0.008744   Median :0.3554   Median :1.9332   Median : 86.0  
 Mean   :0.011539   Mean   :0.3786   Mean   :2.0351   Mean   :113.5  
 3rd Qu.:0.012303   3rd Qu.:0.4495   3rd Qu.:2.3565   3rd Qu.:121.0  
 Max.   :0.074835   Max.   :0.6600   Max.   :3.9565   Max.   :736.0  

mining info:
      data ntransactions support confidence
 Groceries          9835   0.006       0.25

summary(rules)的解释：
第一段：规则的条数，共有463条规则
第二段：规则长度的分布，len=2有150条规则，len=3有297，len=4有16。
第三段：规则长度的五数总括和均值。
第四段：支持度、置信度和lift的五数总括和均值。
第五段：挖掘的相关信息。

（3）评估规则

规则可以划分为3大类：

• 提供非常清晰、有用的洞察，可以直接应用在业务上。
• 显而易见，很清晰但是没啥用，属于common sense，如 {尿布} => {婴儿食品}。
• 不清晰，难以解释，需要额外的研究来判定是否是有用的rule。

那么，如何发现有用的rules呢？

• 按照某种度量对规则进行排序。

> #按照lift，对规则进行排序
> orderbylift_rules <- sort(rules, by = 'lift')
> inspect(orderbylift_rules[1:5])
    lhs                   rhs                      support confidence     lift count
[1] {herbs}            => {root vegetables}    0.007015760  0.4312500 3.956477    69
[2] {berries}          => {whipped/sour cream} 0.009049314  0.2721713 3.796886    89
[3] {tropical fruit,                                                                
     other vegetables,                                                              
     whole milk}       => {root vegetables}    0.007015760  0.4107143 3.768074    69
[4] {beef,                                                                          
     other vegetables} => {root vegetables}    0.007930859  0.4020619 3.688692    78
[5] {tropical fruit,                                                                
     other vegetables} => {pip fruit}          0.009456024  0.2634561 3.482649    93

• 按照条件搜索规则

items %in% c(“A”, “B”)表示 lhs+rhs的项集并集中至少有一个item在c(“A”, “B”)中。
如果仅仅想搜索lhs或者rhs，那么用lhs或rhs替换items即可。如：lhs %in% c(“yogurt”)。
%in%是精确匹配
%pin%是部分匹配，也就是说只要item like ‘%A%’ or item like ‘%B%’
%ain%是完全匹配，也就是说itemset has ’A’ and itemset has ‘B’
同时可以通过条件运算符(&, |, !) 添加 support, confidence, lift的过滤条件。

> #按条件筛选关联规则
> subsetrules <- subset(rules, subset = rhs %in% "whole milk" & lift >= 2)
> inspect(sort(subsetrules, by = "support")[1:5])
    lhs                             rhs          support    confidence lift     count
[1] {other vegetables,yogurt}    => {whole milk} 0.02226741 0.5128806  2.007235 219  
[2] {tropical fruit,yogurt}      => {whole milk} 0.01514997 0.5173611  2.024770 149  
[3] {root vegetables,yogurt}     => {whole milk} 0.01453991 0.5629921  2.203354 143  
[4] {pip fruit,other vegetables} => {whole milk} 0.01352313 0.5175097  2.025351 133  
[5] {root vegetables,rolls/buns} => {whole milk} 0.01270971 0.5230126  2.046888 125  

• 查看其它的quality measure

这里一般用到另外两种测度指标：
coverage：规则左边的支持度，衡量规则应用的频率。
chiSquared：卡方统计量，为了检验规则的lhs和rhs之间的独立性。在α= 0.05时，具有1个自由度（2×2列联表）的卡方分布的临界值是3.84；较高的卡方值表明lhs和rhs不是独立的，也就是该值越大，表示关联规则越可信。
还有很多种测度指标，具体可以看帮助?interestMeasure。

> #查看其它的quality measure
> qualityMeasures <- interestMeasure(subsetrules, measure = c("coverage", "chiSquared"), transactions = Groceries)
> summary(qualityMeasures)
    coverage          chiSquared    
 Min.   :0.009964   Min.   : 43.35  
 1st Qu.:0.011845   1st Qu.: 60.16  
 Median :0.014642   Median : 73.63  
 Mean   :0.016264   Mean   : 77.80  
 3rd Qu.:0.017743   3rd Qu.: 91.90  
 Max.   :0.043416   Max.   :155.43  
> quality(subsetrules) <- cbind(quality(subsetrules), qualityMeasures)  #将coverage和chiSquared统计量加入到quality(subsetrules)中
> inspect(head(sort(subsetrules, by = "chiSquared")))
    lhs                                 rhs          support     confidence lift     count coverage  
[1] {other vegetables,yogurt}        => {whole milk} 0.022267412 0.5128806  2.007235 219   0.04341637
[2] {root vegetables,yogurt}         => {whole milk} 0.014539908 0.5629921  2.203354 143   0.02582613
[3] {butter,yogurt}                  => {whole milk} 0.009354347 0.6388889  2.500387  92   0.01464159
[4] {tropical fruit,root vegetables} => {whole milk} 0.011997966 0.5700483  2.230969 118   0.02104728
[5] {tropical fruit,yogurt}          => {whole milk} 0.015149975 0.5173611  2.024770 149   0.02928317
[6] {other vegetables,butter}        => {whole milk} 0.011489578 0.5736041  2.244885 113   0.02003050
    chiSquared
[1] 155.4279  
[2] 129.5825  
[3] 112.9113  
[4] 109.9678  
[5] 106.9339  
[6] 106.9239 

（4）将规则写出

#写出关联规则
> write(subsetrules, file="subsetrules.csv", sep=",", quote=TRUE, row.names=FALSE)

说明：本文仅作学习使用。在R语言实战部分大部分借鉴了博文R语言 | 关联规则，在此感谢原作者，由于R语言可视化部分还没有深入了解，所以原文中的进阶部分没有深入探讨，有需要的童鞋请看原文。

参考资料：
【1】数据挖掘概念与技术
【2】R语言之Apriori算法应用
【3】R语言 | 关联规则