【线段树学习】POJ-3468-A Simple Problem with Integers

A Simple Problem with Integers

Description
You have N integers, A1, A2, … , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.

Input
The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A1, A2, … , AN. -1000000000 ≤ Ai ≤ 1000000000.
Each of the next Q lines represents an operation.
“C a b c” means adding c to each of Aa, Aa+1, … , Ab. -10000 ≤ c ≤ 10000.
“Q a b” means querying the sum of Aa, Aa+1, … , Ab.

Output
You need to answer all Q commands in order. One answer in a line.

Sample Input
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

Sample Output
4
55
9
15

#include 
#define N 111111

#define LL long long
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1

LL add[N<<2];
LL sum[N<<2];

void PushUP(int rt)
{
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}

void PushDown(int rt,int m)
{
    if(add[rt])
    {
        add[rt<<1]+=add[rt];
        add[rt<<1|1]+=add[rt];
        sum[rt<<1]+=(m-(m>>1))*add[rt];
        sum[rt<<1|1]+=(m>>1)*add[rt];
        add[rt]=0;
    }
}

void Build(int l,int r,int rt)
{
    add[rt]=0;
    if(l==r)
    {
        scanf("%lld",&sum[rt]);
        return;
    }
    int m=(l+r)>>1;
    Build(lson);
    Build(rson);
    PushUP(rt);
}

void Update(int L,int R,int c,int l,int r,int rt)
{
    if(L<=l&&R>=r)
    {
        add[rt]+=c;
        sum[rt]+=(LL)c*(r-l+1);
        return;
    }
    PushDown(rt,r-l+1);
    int m=(l+r)>>1;
    if(L<=m)
        Update(L,R,c,lson);
    if(R>m)
        Update(L,R,c,rson);
    PushUP(rt);
}

LL Query(int L,int R,int l,int r,int rt)
{
    if(L<=l&&R>=r)
        return sum[rt];
    PushDown(rt,r-l+1);
    int m=(l+r)>>1;
    LL ret=0;
    if(L<=m)   ret+=Query(L,R,lson);
    if(R>m)    ret+=Query(L,R,rson);
    return ret;
}

int main()
{
    int m,n;
    scanf("%d%d",&n,&m);
    Build(1,n,1);
    while(m--)
    {
        char s[5];
        int a,b,c;
        scanf("%s",s);
        if(s[0]=='Q')
        {
            scanf("%d%d",&a,&b);
            printf("%lld\n",Query(a,b,1,n,1));
        }
        else
        {
            scanf("%d%d%d",&a,&b,&c);
            Update(a,b,c,1,n,1);
        }
    }
    return 0;
}

模板题，初学，感觉还是很难理解的。
照着大神们的模板学的

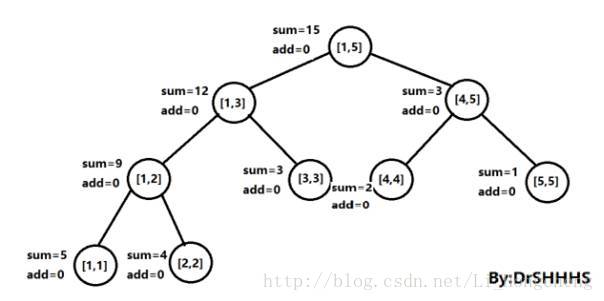
延迟标记在我们需要时，才向下传递信息，如果没有用到，则不再进行操作。这个思想使处理的复杂度依然保持在O（log2(n))左右，相比朴素算法大大地降低了复杂度。
为了完成这种操作，我们可以在结构体中，增加一个add数组存储区间的延迟变化量

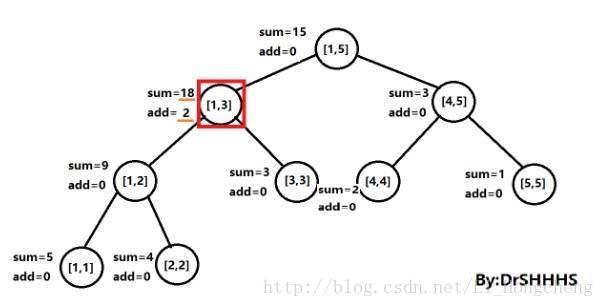
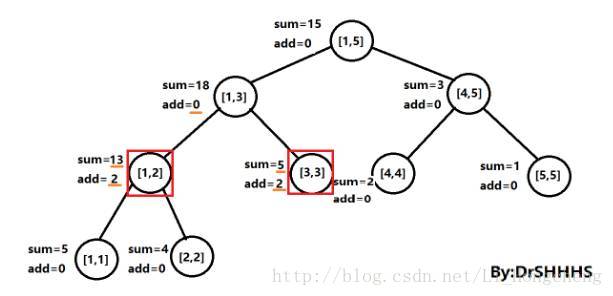
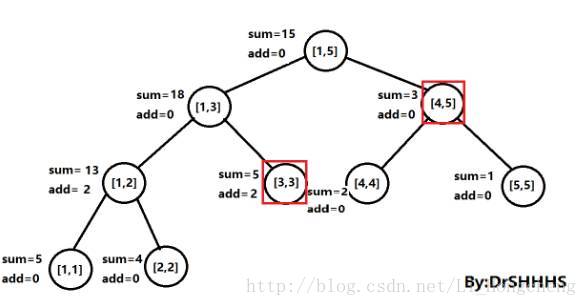
比如现在需要对[a,b]区间值进行加c操作，那么就从根节点[1,n]开始调用update函数进行操作，如果刚好执行到一个子节点，它的节点标记为rt，这时tree[rt].l == a && tree[rt].r == b 这时我们可以一步更新此时rt节点的sum[rt]的值，sum[rt] += c * (tree[rt].r - tree[rt].l + 1)，注意关键的时刻来了，如果此时按照常规的线段树的update操作，这时候还应该更新rt子节点的sum[]值，而Lazy思想恰恰是暂时不更新rt子节点的sum[]值，到此就return，直到下次需要用到rt子节点的值的时候才去更新，这样避免许多可能无用的操作，从而节省时间 。

#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1

宏定义左儿子lson和右儿子rson，貌似用宏的速度要慢。
PushUp(rt)：通过当前节点rt把值递归向上更新到根节点
PushDown(rt)：通过当前节点rt递归向下去更新rt子节点的值
rt表示当前子树的根(root),也就是当前所在的结点