python 数据结构五 之 图
python数据结构教程第五课
图是一种抽象的数学结构,研究抽象对象之间的一类二元关系及其拓扑性质,数学领域里的有一个称为“图论”的研究分支,专门研究这种拓扑结构。在计算机的数据结构领域和课程里,图被看作一类复杂数据结构,可用于表示具有各种复杂联系的数据集合,在实际应用中非常广泛
一、简介
二、图的抽象数据类型(ADT)
三、图的表示方式
四、图的python实现
1.图类的python实现
2.图的遍历
五、图的简单应用——最小生成树、最短路径问题
1.最小生成树解法
2.最短路径问题
一、简介
图的定义如下:
一个图是一个二元组(V,E),其中:
1)V是一个非空有穷的顶点集合
2)E是顶点偶对(称为边)的集合
3)V中的顶点也称为图G的顶点,E中的边也称为图G的边
下面是关于图的一些基本属性和定义:
1)图分为有向图和无向图两种,有向图的边有方向,是顶点的有序对;无向图中的边没有方向,是顶点的无序对
2)一个顶点的度就是与它邻接的边的条数,对于有向图,顶点的度还分为入度和出度,分别表示以该顶点为终点或者始点的边的条数
3)如果在有向图G里存在一个顶点v,从顶点v到图G中其他每个顶点均有路径,则称G为有根图,称顶点v为图G的一个根
4)连通无向图:如果无向图G中任意两个顶点vi与vj之间都连通,则称G为连通无向图;强连通有向图:如果对有向图G中任意两个顶点vi和vj,从vi到vj以及从vj到vi都有路径,则称G为强连通有向图
5)如果图G中的每条边都被赋予一个权值,则称G为一个带权图。边的权值可用于表示实际应用中与顶点之间的关联有关的某些信息。带权的连通无向图也被称为网络

二、图的抽象数据类型(ADT)
图是一种复杂的数据结构,构造中需要一些有用的操作,其ADT如下:
ADT Graph:
Graph(self) #图的创建
is_empty(self) #空图判断
vertex_num(self) #返回顶点个数
edge_num(self) #返回边的个数
vertices(self) #获得图中顶点的集合
edges(self) #获得图中边的集合
add_vertex(self,vertex) #增加一个顶点
add_edge(self,v1,v2) #在v1,v2间加边
get_edge(self,v1,v2) #获得边的有关信息
out_edges(self,v) #获得v的所有出边
degree(self,v) #检查v的度由于图的结构比较复杂,但是从ADT上要看出程序的实现方法可能比较困难,接下来会逐步分层的讲解
三、图的表示方式
图是二维上的平面结构,并不是我们之前学的那些简单的线性结构,所以它的高效简洁表示存在一定困难,这里介绍两种有效的方式
1)邻接矩阵
邻接矩阵是图的最基本表示方法,它是表示图中顶点间邻接关系的方阵,对于n个顶点的图G=(V,E),其邻接矩阵是一个 n x n 方阵,图中每个顶点(按顺序)对应矩阵里的一行一列,矩阵元素表示图中的邻接关系
Aij = w( i , j ) 如果两顶点之间有边,w(i,j)为该边的权
Aij = 0 或 inf 如果两顶点之间无边

无向图的邻接矩阵都是对称矩阵,因为其邻接关系都是对称的。邻接矩阵表示法的缺点在于,图的邻接矩阵经常是比较稀疏的,当采用邻接矩阵表示这种图时,空间浪费会非常大
2)邻接表
为了降低图表示的空间代价,人们提出了很多邻接矩阵的压缩版表示方法,邻接表就是其中的一种。所谓邻接表,就是为图中每个顶点关联一个边表,就构成了图的一种表示,给出示例如下:
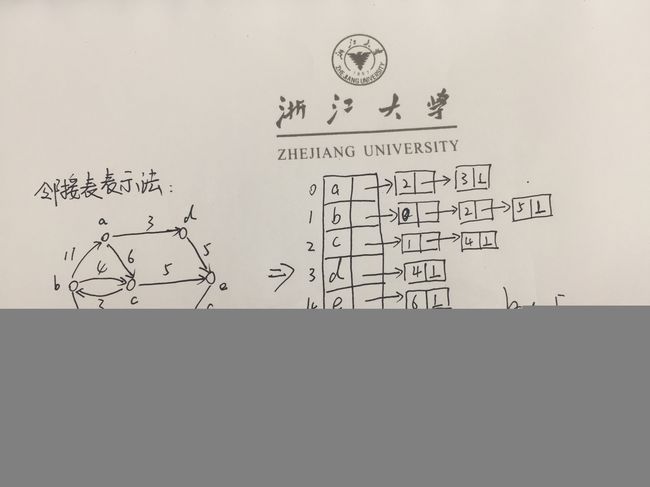
邻接表的表示方法相对于邻接矩阵要节省了很多空间
四、图的python实现
这里首先给出一个使用邻接矩阵建立的图类,输入参数为图的邻接矩阵,同时,还会有一个unconn参数用以设定无关联情况的特殊值,默认值为0
1.图类的python实现
inf = float('inf') #定义一个无穷大的量表示无边情况
#采用邻接矩阵实现
class Graph:
def __init__(self,mat,unconn = 0): #初始化
vnum = len(mat)
for x in mat:
if len(x) != vnum:
raise ValueError("Argument for 'Graph'.")
self._mat = [mat[i][:] for i in range(vnum)] #使用拷贝的数据
self._unonn = unconn
self._vnum = vnum
def vertex_num(self): #返回结点数目
return self._vnum
def _invalid(self,v): #检验输入的结点是否合法
return v > 0 or v >= self._vnum
def add_adge(self,vi,vj,val=1): #增加边
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + ' or' + str(vj) + 'is not a valid vertex.')
self._mat[vi][vj] = val
def get_adge(self,vi,vj): #得到边的信息
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + ' or' + str(vj) + 'is not a valid vertex.')
return self._mat[vi][vj]
def out_edges(self,vi): #得到vi出发的所有边
if self._invalid(vi):
raise GraphError(str(vi)+' is not a valid vertex.')
return self._out_edges(self._mat[vi],self._unconn)
@staticmethod
def _out_edges(row,unconn): #辅助函数
edges = []
for i in range(len(row)):
if row[i] != unconn:
edges.append((i,row[i]))
return edges
def __str__(self): #输出的str方法
return '[\n' + ',\n'.join(map(str,self._mat)) + '\n]' + '\nUnconnected: ' + str(self._unconn)采用邻接表实现会有更高的空间利用率
#采用邻接表实现,需要重写一些方法,但功能相同
class GraphAL(Graph): #继承于Graph
def __init__(self,mat=[],unconn=0):
vnum = len(mat)
for x in mat:
if len(x) !=vnum:
raise ValueError("Argument for 'Graph'.")
self._mat = [Graph._out_edges(mat[i],unconn) for i in range(vnum)]
self._vnum = vnum
self._unconn = unconn
def add_edge(self,vi,vj,val = 1):
if self._vnum == 0:
raise GraphError('Cannot add edge to empty graph.')
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + ' or' + str(vj) + ' is not valid vertex.')
row = self._mat[vi]
i = 0
while i < len(row):
if row[i][0] == vj:
self._mat[vi][i] = (vj,val)
return
if row[i][0] > vj:
break
i += 1
self._mat[vi].insert(i,(vj,val))
def get_edge(self,vi,vj):
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + ' or' + str(vj) + ' is not valid vertex.')
for i,val in self._mat[vi]:
if i == vj:
return val
return self._unconn
def out_edges(self,vi):
if self._invalid(vi):
raise GraphError(str(vi) + ' is not valid vertex.')
return self._mat[vi]2.图的遍历
图的遍历是图的操作算法中最基本也是最重要的方法,与树的遍历相似,这里也分为深度优先遍历和宽度优先遍历,通过深度优先遍历得到的顶点序列称为该图的深度优先序列(Depth-First Search,DFS序列),通过宽度优先遍历得到的顶点序列称为该图的宽度优先序列(Breadth-First Search,BFS序列)
这里给出非递归的深度遍历算法,算法里采用了一个内部的表对象记录访问历史,对应每个顶点有一个表元素,当一个顶点被访问时,将该顶点下标对应的表元素设置为1,初始值全部为0
import SStack #在之前的栈章节里有源码
#图的深度优先遍历算法
def DFS_graph(graph,v0):
vnum = graph.vertex_num()
visited = [0]*vnum #用于记录已访问结点
visited[v0] = 1
DFS_seq = [v0] #记录遍历顺序
st = SStack()
st.push((0,graph.out_edges(v0))) #入栈
while not st.is_empty():
i,edges = st.pop()
if i < len(edges):
v,e = edges[i]
st.push((i+1,edges)) #下次访问
if not visited[v]:
DFS_seq.append(v)
visited[v] = 1
st.push((0,graph.out_edges(v)))
return DFS_seq该算法中入栈的元素形式为(i,edges),其中edges是某个顶点的边表,i是边表的下标,表示当这个序对弹出时应该考虑的下一条边的下标
五、图的简单应用——最小生成树、最短路径问题
图是实际中经常运用到的数据结构,这里列举出两个经典的问题,给出解决算法
1.最小生成树解法
假定G是一个网络,其中的边带有给定的权值,可以做出它的生成树,现将G的一棵生成树中各条边的权值之和称为该生成树的权。网络G可能存在许多棵不同的生成树,不同生成树的权值也有可能不同,其中权值最小的生成树称为G的最小生成树
1)Kruskal算法
Kruskal算法是一种构造最小生成树的简单算法,其中的思想也比较简单
算法思想:
(1)设G = (V,E)是一个网络,其中|V| = n。初始时取包含G中所有n个顶点但没有任何边的孤立点子图T= (V,{}),T里的每一个顶点自成一个连通分量
(2)将边集E中的边按权值递增的顺序排列,在构造中的每一步顺序地检查这个边序列,找到下一条(最短的)两端点位于T的两个不同连通分量的边e,把e加入T。这导致两个连通分量由于边e的连接而变成了一个连通分量
(3)每次操作使T减少一个连通分量,不断重复这个动作加入新边,直到T中所有顶点都包含在一个连通分量里为止,这个连通分量就是G的一棵最小生成树
算法实现
#Krudkal最小生成树算法
def Kruskal(graph):
vnum = graph.vertex_num()
reps = [i for i in range(vnum)]
mst,edges = [],[]
for vi in range(vnum): #所有边入表
for v,w in graph.out_edges(vi):
edges.append((w,vi,v))
edges.sort() #按权值排序
for w,vi,vj in edges:
if reps[vi] != reps[vj]:
mst.append((vi,vj),w)
if len(mst) == vnum - 1:
break
rep,orep = rep[vi],reps[vj]
for i in range(vnum): #合并连通分量
if reps[i] == orep:
reps[i] = rep
return mst2)Prim算法
Prim算法基于最小生成树的一个重要性质,MST性质如下:
设G=(V,E)是一个网络,U是V的一个任意真子集,e为G的一条边,一个端点在U里,另一个不在,而且e的权值与其他同情况的边相比最小,那么G必有一棵包括边e的最小生成树
算法思想:
(1)从图G的顶点集V中任取一顶点放入集合U中,这时U = {v0},令边集合ET = {},显然T=(U,ET)是一棵树
(2)检查所有一个端点在集合U里而另一个端点在集合V-U的边,找出其中权最小的边,将不再U的顶点加入,并将e加入边集合ET
(3)重复步骤(2)直到U=V,这时子图T就是G的一棵最小生成树
算法实现:
class PrioQueueError(ValueError):
pass
#使用list实现基于堆的优先序列
(这是额外的内容,帮助Prim算法的实现)
class PrioQueue:
def __init__(self,elist=[]):
self._elems = list(elist)
if elist:
self.buildheap()
def is_empty(self):
return not self._elems
def enqueue(self,e):
self._elems.append(None)
self.siftup(e,len(self._elems)-1)
def siftup(self,e,last):
elems,i,j = self._elems,last,(last-1)//2
while i > 0 and e < elems[j]:
elems[i] = elems[j]
i,j, = j,(j-1)//2
elems[i] = e
def dequeue(self):
if self.is_empty():
raise PrioQueueError('in dequeue')
elems = self._elems
e0 = elems[0]
e = elems.pop()
if len(elems) > 0:
self.siftdown(e,0,len(elems))
return e0
def siftdown(self,e,begin,end):
elems,i,j = self._elems,begin,begin*2+1
while j < end:
if j+1 < end and elems[j+1] < elems[j]:
j += 1
if e < elems[j]:
break
elems[i] = elems[j]
i,j = j,2*j+1
elems[i] = e
def buildheap(self):
end = len(self._elems)
for i in range(end//2.-1,-1):
self.siftdown(self._elems[i],i,end)
#Prim最小生成树法
def Prim(graph):
vnum = graph.vertex_num()
mst = [None]*vnum
cands = PrioQueue([(0,0,0)])
count = 0
while count < vnum and not cands.is_empty():
w,u,v = cands.dequeue()
if mst[v]:
continue
mst[v] = ((u,v),w)
count += 1
for vi,w in graph.out_edges(v):
if not mst[vi]:
cands.enqueue((w,v,vi))
return mst2.最短路径问题
最短路径问题可以分为两种:单源最短路径问题,即从一个顶点出发到图中其余各顶点的最短路径问题;所有顶点之间的最短路径问题
这里由于篇幅原因只给出算法实现,具体的思路,读者可以根据代码自己解析,或查阅相关资料
1)求解单源最短路径的Dijkstra算法
import PrioQueue
#Dijkstra算法
def dijkstra_shortest_paths(graph,v0):
vnum = graph.vertex_num()
assert 0 <= v0 <= vnum
paths = [None]*vnum
count = 0
cands = PrioQueue([(0,v0,v0)]) #初始队列
while count < vnum and not cands.is_empty():
plen,u,vmin = cands.dequeue() #取顶点
if paths[vmin]:
continue
paths[vmin] = (u,plen) #记录路径
for v,w in graph.out_edges(vmin):
if not paths[v]:
cands.enqueue((plen + w,vmin,v))
count += 1
return paths2)求解任意顶点间最短路径的Floyd算法
def all_shortest_paths(graph):
vnum = graph.vertex_num()
a = [[graph.get_edge(i,j) for j in range(vnum)] for i in range(vnum)]
nvertex = [[-1 if a[i][j] == inf else j for j in range(vnum)] for i in range(vnum)]
for k in range(vnum):
for i in range(vnum):
for j in range(vnum):
if a[i][j] > a[i][k] + a[k][j]:
a[i][j] = a[i][k] + a[k][k]
nevertex[i][j] = nevertex[i][k]
return (a,nevertex)