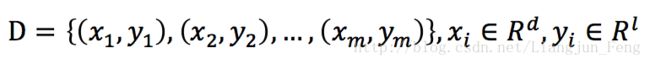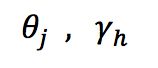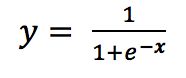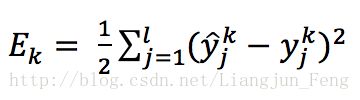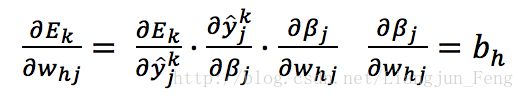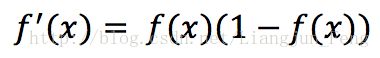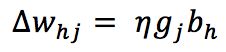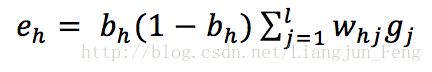机器学习教程 之 人工神经网络的前世今生：标准BP神经网络原理

参考了一些书籍和博客，整理了关于神经网络的简单发展历史，给出BP神经网的计算原理与python3源码，供对相关领域感兴趣的小伙伴学习

一、神经网络发展的沉浮
二、BP神经网络算法原理
三、BP神经网络算法python3实现

一、神经网络发展的沉浮

早在二十世纪四十年代M-P神经元模型、Hebb学习率等相关理论便发展起来，1949年神经心理学家Hebb出版《行为组织学》（Organization of Behavior)，在该书中，Hebb提出了被后人称为“Hebb规则”的学习机制。这个规则认为如果两个细胞总是同时激活的话，它们之间就有某种关联，同时激活的概率越高，关联度也越高，这是神经网络理论较为早期的一些积淀。

唐纳德·赫布

神经网络研究的后一个大突破是1957年。康奈尔大学的实验心理学家弗兰克·罗森布拉特在一台IBM-704计算机上模拟实现了一种他发明的叫作““感知机”（Perceptron）的神经网络模型。这个模型可以完成一些简单的视觉处理任务。这引起了轰动。罗森布拉特在理论上证明了单层神经网络在处理线性可分的模式识别问题时，可以收敛，并以此为基础，做了若干“感知机”有学习能力的实验。罗森布拉特1962年出了本书：《神经动力学原理：感知机和大脑机制的理论》（Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms），这书总结了他的所有研究成果，成为当时的圣经。

弗兰克·罗森布拉特

然而MIT计算机科学研究之父、人工智能的奠基人，达特茅斯会议的组织者马文·闵斯基（Marvin Minsky,1927-2016，于1969年获得图灵奖）与Seymour Papert在1969年出版的《感知机》一书中指出，单层神经网络无法解决非线性问题，而多层网络的训练算法尚看不到希望。“感知机”的缺陷被明斯基以一种敌意的方式呈现，当时对罗森布拉特是致命打击。1971年，罗森布拉特四十三岁生日那天，在划船时淹死。很多人认为他是自杀。闵斯基的论断直接使神经网络的研究进入了“冰河时期”，美国和苏联均停止了对神经网络研究的资助，全球该领域研究人员纷纷转行，仅极少数人坚持下来。哈佛大学的Paul Werbos在1974年发明BP算法时，正值神经网络冰河时期，因此并未受到应有的重视。

年轻时候的闵斯基

1983年，加州理工学院的物理学家John Hopfield利用神经网络，在旅行商问题这个NP完全问题求解上获得了当时的最好结果，引起了轰动。随后，USCD的David Rumelhart 与James McClelland领导的PDP小组出版了《并行分布处理：认知微结构的探索》一书，在该书中，Rumelhart等人重新发明了BP算法，由于当时正处于Hopfield引起的轰动中，BP算法迅速走红，这掀起了神经网络的第二次高潮。然而，在二十世纪九十年代中期，随着统计学习理论和支持向量机的兴起，由于神经网络学习的理论性质并不清楚、试错性强、在使用中充斥着大量“窍门”的弱点，国际上对于神经网络的研究再一次进入低谷，当时NIPS会议甚至不接受以神经网络为主题的论文。

物理学家霍普菲尔德
在2010年前后，随着计算能力的迅猛提升和大数据的涌现，对于神经网络研究，又在“深度学习”的大旗下重新崛起，在ImageNet等若干竞赛上以大优势夺冠，此后google、百度、facebook等公司纷纷投入巨资对相关理论进行研发，不论是学术界还是工业界都涌现出一大批人工智能弄潮儿，对神经网络的研究进入了三次高潮，史无前例的迈入了“深度学习”时代。

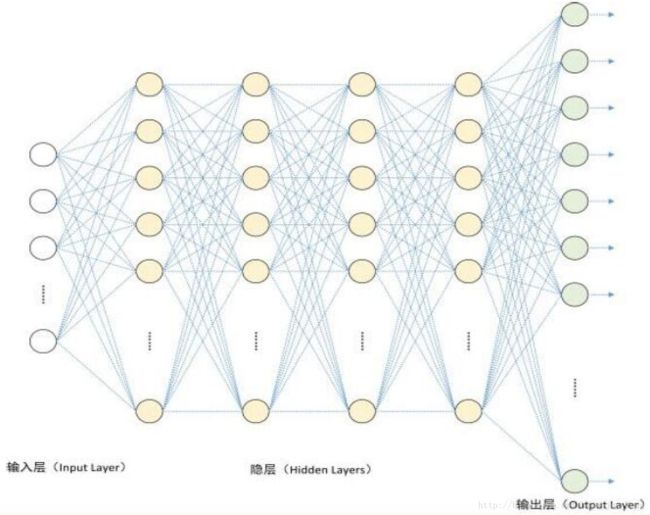
深度学习模型

注：在查资料的时候，我发现这些对人类发展作出杰出贡献，推动历史车轮前进的学者已经不能简单的用才华横溢来形容了。。这里给几个传送门，感兴趣的可以看一下，什么叫超越时代的思想，学术大炮，看完之后，你可能会觉得自己需要买个脑子
马文·闵斯基 ： http://blog.sina.com.cn/s/blog_8a4651600102w48d.html
赫伯特·西蒙： http://www.360doc.com/content/16/0704/11/7479083_572868246.shtml
约翰·麦卡锡： http://www.ituring.com.cn/article/436
参考文献：[1] 周志华.机器学习[M].北京：清华大学出版社，2015: 191～121

二、BP神经网络算法原理

误差逆传播算法（Error BackPropagation，BP）是神经网络算法中的杰出代表，它是迄今为止最成功的神经网络算法，现实任务中使用神经网络时，大多是在是在使用BP算法进行训练。BP算法不仅可以用于多层前馈网络（前馈是指网络拓扑结构上不存在环路或回路），还可以用于其他网络，但通常说到“BP网络”时，是指BP算法训练的多层前馈网络
这里首先对三层（输入层、隐层、输出层）的相关参数给出定义，给定训练集

即输入示例由d个属性描述，输出l维实例向量，现在设定一个拥有d个输入神经元、l个输出神经元、q个隐层神经元的多层前馈神经网络结构，其中输出层第j个神经元的阈值、隐层第h个神经元的阈值分别表示为

输入层第j个神经元与隐层第h个神经元之间的连接权、隐层第h个神经元与输出层第j个神经元之间的连接权分别表示为

由上可得，隐层第h个神经元接收到的输入与输出层第j个神经元接收到的输入可分别表示为

假设隐层和输出层神经元都使用下列的Sigmoid函数做为激活函数

对于一个训练样例，假定神经网络的输出为

即

BP算法基于梯度下降策略，以目标的负梯度方向对参数进行调整，现以均方差定义网络的输出误差为

上式中的1/2只是为了方便求导
在定义的网络中的所有连接权和阈值都需要在确定误差不满足要求后进行更新，更新的估计式为

下面以从隐层到输出层的连接权为例来进行推导，以目标的负梯度方向对参数进行调整，对误差求导并给定学习率，有

又有

已知Sigmoid具有如下性质

综上可得（经过网友，zhaozx19950803，的提醒gj的结果应该多一个负号）

于是可得从隐层到输出层的连接权的更新公式

同理可得

其中

三、BP神经网络算法python3实现

python3源码

#!/usr/bin/env python3
# -*-coding: utf-8-*-
# Author : LiangjunFeng
# Blog   : http://my.csdn.net/Liangjun_Feng
# GitHub : https://www.github.com/LiangjunFeng
# File   : BP neural network.py
# Date   : 2017/09/17 11:12
# Version: 0.1
# Description: BP neural network

import random
import math
import numpy

random.seed(0)
def rand(low,high):   #随机函数
    return (high-low)*random.random()+low

def sigmoid(x):       #sigmoid函数
    return 1.0/(1+math.exp(-x))

def vectorSigmoid(vect):     #对一个向量里的所有值进行sigmoid函数处理
    length = numpy.shape(vect)[1]
    for i in range(length):
        vect[0,i] = sigmoid(vect[0,i])
    return vect

def makeMatrix(length,bordth,fill = 0.0):    #创建矩阵
    mat = []
    for  i in range(length):
        mat.append([fill]*bordth)
    return numpy.mat(mat)

def randfillMatrix(mat,low,high):      #矩阵值的随机填充
    length = numpy.shape(mat)[0]
    bordth = numpy.shape(mat)[1]
    for i in range(length):
        for j in range(bordth):
            mat[i,j] = rand(low,high)
    return mat

def vectorMultiply(vect1,vect2):       #向量相乘得到一个矩阵
    length = numpy.shape(vect1)[1]
    bordth = numpy.shape(vect2)[1]
    mat = makeMatrix(length,bordth)
    for i in range(length):
        for j in range(bordth):
            mat[i,j] = vect1[0,i]*vect2[0,j]
    return mat

class BPNeuralNetwork:               
    def __init__(self,inputNodes,hiddenNodes,outputNodes):    #初始化变量
        self._inputNodes = inputNodes      #输入层结点个数
        self._hiddenNodes = hiddenNodes    #隐藏层结点个数
        self._outputNodes = outputNodes    #输出层结点个数
        self._inputLayer = []              #输入层数据
        self._hiddenLayer = []             #隐藏层数据
        self._outputLayer = []             #输出层数据
        self._inputWeights = []            #输入层到隐藏层连接权
        self._outputWeights = []           #隐藏层到输出层连接权
        self._hiddenThreshold = []         #隐藏层激活阈值
        self._outputThreshold = []         #输出层阈值

    def setup(self):        
        self._inputLayer = makeMatrix(1,self._inputNodes,1.)
        self._hiddenLayer = makeMatrix(1,self._hiddenNodes,1.)
        self._outputLayer = makeMatrix(1,self._outputNodes,1.)    #三层网络架构初始赋值

        self._hiddenThreshold = makeMatrix(1,self._hiddenNodes,1.)
        self._outputThreshold = makeMatrix(1,self._outputNodes,1.)    #两层激活阈值初始赋值

        self._inputWeights = makeMatrix(self._inputNodes,self._hiddenNodes)
        self._outputWeights = makeMatrix(self._hiddenNodes,self._outputNodes)  #创建权重矩阵

        self._inputWeights = randfillMatrix(self._inputWeights,-1.,1.)
        self._outputWeights = randfillMatrix(self._outputWeights,-1.,1.)    #权重矩阵初始随机幅值

    def getInput(self,_input):                #将一个输入赋值到输入层
        for i in range(self._inputNodes):
            self._inputLayer[0,i] = _input[i]

    def predict(self,_input):                 #根据输入输出预测值到输出层
        self.getInput(_input)
        self._hiddenLayer = vectorSigmoid(self._inputLayer*self._inputWeights - self._hiddenThreshold)
        self._outputLayer = vectorSigmoid(self._hiddenLayer*self._outputWeights - self._outputThreshold)

    def backPropagation(self,y,lRate):       #反响传播更新激活阈值与连接权    
        G = numpy.multiply(numpy.multiply(self._outputLayer,1-self._outputLayer),y-self._outputLayer)
        self._outputWeights = self._outputWeights + lRate*vectorMultiply(self._hiddenLayer,G)
        self._outputThreshold = self._outputThreshold - lRate*G
        E = numpy.multiply(numpy.multiply(self._hiddenLayer,1-self._hiddenLayer),(self._outputWeights*G.T).T)
        self._inputWeights = self._inputWeights + lRate*vectorMultiply(self._inputLayer,E)
        self._hiddenThreshold = self._hiddenThreshold - lRate*E
        return float((y-self._outputLayer)*(y-self._outputLayer).T) 

    def fit(self,input_,y_,limit = 10000,accuracy = 0.001,lRate = 0.2):     #拟合数据
        self.setup()
        num = len(input_)
        error,times = num,1
        while((error > accuracy) and (times < limit)):
            i,error = 0,0 
            while(i < num):
                _input = input_[i]
                y = y_[i]
                self.predict(_input)
                error += self.backPropagation(y,lRate)               
                i += 1
            times += 1 

if __name__ == '__main__':           #以异或运算举例
    nn = BPNeuralNetwork(2,7,1)        
    cases = [[0,0],[0,1],[1,0],[1,1]]
    labels = [[0],[1],[1],[0]]        
    nn.fit(cases,labels)
    for case in cases:
        nn.predict(case)
        print(case,'  ',nn._outputLayer)