树状数组--快速计算动态前缀和
文章目录
- 问题 && 结论
- 原理
- 实现
- 进阶操作
问题 && 结论
树状数组是一种能够维护动态数组并快速计算动态前缀和的数据结构.
假设有一数组A[n],(A[1]表示数组第一个元素),现对A[n]分别进行如下操作m次:
- 给一i(1 <= i <= n),将A[i]的值加上/减去某个数k;
- 给一i(1 <= i <= n),求A[1]+A[2]+A[3]+…+A[i];
暴力解法:对于1,时间复杂度为O(m),对于2,时间复杂度为O(mn);
树状数组:对于1,时间复杂度为O(mlog(n-i)),对于2,时间复杂度为O(mlogn);
即对于动态数组A[n+1],当m很大时,树状数组能够在很优秀的时间复杂度上求出其前缀和,原理下面讲解.
原理
动态数组:与其对立的是静态数组,动态数组是指数组元素值会经常发生变化的数组.
因为上题的操作1,导致A[n+1]是一个动态数组,在操作2上对暴力解法常规的优化–预处理前缀和就行不通了
树状数组其实也是一个前缀和数组,但是它和静态前缀和数组不一样,它是基于二进制的原理,并且能够很灵活地维护动态数组带来的动态前缀和.因为采用了二进制,所以树状数组相关的操作都是O(logn)级别的,是一个很优秀的复杂度,我们先看几个例子,再来讲解原理.
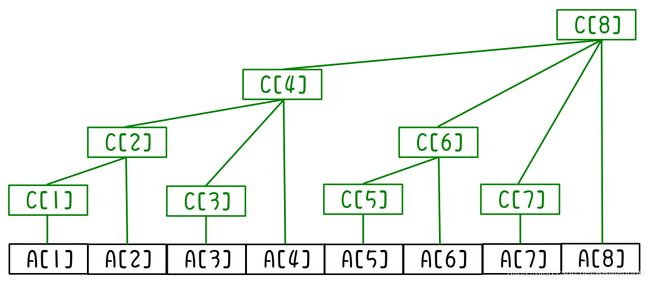
如下图,假设我们有一个A[8],在此数组上建立的树状数组C[8]形态如下:
上图的含义为:
- C[1] = A[1];
- C[2] = A[1] + A[2];
- C[3] = A[3];
- …
- C[8] = A[1] + A[2] + … + A[8];
这个结构的树状数组像不像一棵树?当然树状数组也是因此得名.上面只是一个演示,为了更方便说明问题,我们以一个A[16]的树状数组来说明,并画成另一种我更喜欢的形式:
怎么样?是不是马上就能想到一个相似的模型–二分?由于使用二进制的关系,导致树状数组的形态图和二分类似,这也是正常的现象.那么根据这个树状数组,我们可以实现一些操作,先从操作2说起,比如:
我们要求A[1] + A[2] + … + A[13]的前缀和,则对树状数组进行如下处理:
很巧妙,对吧.是巧合吗?当然不是,实际上对于任意一个前缀和,在树状数组中都能用上述方法求出.实际上我们可以通过另一个"巧合"来说明上述做法的正确性:
| 二进制数 | 末尾0的个数 | 累加的数 | 累加数的个数 |
|---|---|---|---|
| 1101 | 0 | A[13] | 1 = 20 |
| 1100 | 2 | A[12],A[11],…,A[9] | 4 = 22 |
| 1000 | 3 | A[8],A[7],…,A[0] | 8 = 23 |
可以看到,1 + 4 + 8 = 13,经过上述操作最后的确是一共加了13个数.这便说明这样的设计不是巧合.那么到底是为什么?在一探究竟之前,我们来看看树状数组是如何进行操作1的,比如:
我们想要修改A[6]的值,则对树状数组进行如下处理:
其实这个操作1就是上面操作2的逆操作,是不是也非常神奇?这里还有几点需要说明:
- 可以只维护树状数组而不维护原数组,如果需要对原数组进行单点查询操作,才需要维护原数组
- 树状数组维护动态数组的过程不是O(1)的复杂度,但是为了快速求前缀和,这么点时间的牺牲是绝对划算的
以上,就是树状数组两个操作的原理.
实现
从上述两个操作看来,我们知道树状数组非常依赖一个东西:二进制,进一步讲,是二进制数最低位的1的位置.关于最低位的1,让我们换个角度考虑一下:
- 在最低位的1减去1,相当于减去一个以最低位1为最高位,其余位都是0的二进制数.
- 在最低位的1加上1,相当于加上一个以最低位1为最高位,其余位都是0的二进制数.
我知道,看起来像两句废话.但是,这个操作却是可行的,我们可以通过一个lowbit(x)函数解决这个问题:
int lowbit(int x) {
return x & -x; //返回以x最低位1为最高位,其余位都是0的二进制数对应的十进制数;
}
这样我们就能求出这个数了!至于原理嘛,如下:
- 设(X)10 = 13,则X补 = 01101,(-X)补 = 10011,则(X & -X)补 = (00001)2 = (1)10
- 而以13的二进制数的最低位1为最高位,其余位都是0的二进制数的十进制形式正是1,即lowbit(13) = 1
- 同理lowbit(12) = 4,lowbit(8) = 8.因此才有13 - 1 = 12;12 - 4 = 8;8 - 8 = 0;满足上述操作
有了lowbit(x)这个函数,我们就可以直接实现树状数组的两种操作了,实现如下:
int bit[100005],num[100005],n; //bit[]为树状数组,num[]为原数组,n为数组长度;
int lowbit(int x) {
return x & -x;
}
int query(int i) { //查询前缀和,1,2,...,i;
int sum = 0;
while(i > 0) {
sum += bit[i];
i -= lowbit(i);
}
return sum;
}
int getSum(int le,int ri) { //区间求和,求num[le,ri]的和;
return query(ri) - query(le-1);
}
void add(int i,int x) { //将num[i]的值加上x;
while(i <= n) {
bit[i] += x;
i += lowbit(i);
}
}
我们讲了半天都没有将树状数组实现,而是假定我们已经有了树状数组,会进行怎么样的操作.有了add(i,x)不仅可以将num[i]加上x,还可以"无中生有"–实现一个最初版本的树状数组.如:
//以下内容重用了上述代码,其意义不再赘述;
memset(bit,0,sizeof bit); //先将树状数组清空;
for(int i = 1; i <= n; i++) {
cin>>num[i];
add(i,num[i]); //将初始值加到树状数组上去;
}
以上就是树状数组基本功能的实现,说一个注意的点:位运算只能用于整型操作数,但是树状数组妙就妙在:我们是对数组下标进行按位与运算的,因此无论树状数组维护什么类型的动态数组,都是可以做到的.
注意我们还有getSum(le,ri)这个函数,树状数组虽然基本操作是求前缀和,但是运用中往往查询区间和要比查询前缀和更常用得多,因此我们说树状数组的基本操作是:单点修改,区间查询.
进阶操作
树状数组除了可以实现区间查询和单点修改的操作以外,还有一些进阶操作:单点查询以及区间修改.
说是进阶操作,其实也是树状数组非常简单的一个应用.首先我们要引入一类问题:
假设有一数组A[n],(A[1]表示数组第一个元素),现对A[n]分别进行如下操作m次:
- 给定le,ri(1 <= le <= ri <= n),将A[n]中区间[le,ri]内的元素同时加上/减去某个数k.
- 给定i(1 <= i <= n),求A[i]的值.
为了解决这个问题,就必须先引入一个差分数组的概念,其定义如下:
存在一数组A[n],其差分数组d[n]满足:
- d[1] = A[1];
- d[i] = A[i] - A[i-1],(2 <= i <= n);
差分数组的性质如下:
- 当i = 1时,d[1] = A[1];
- 当i ∈ \in ∈[2,n]时,A[i] = d[i] + A[i-1] = d[i] + d[i-1] + A[i-2] = d[i] + d[i-1] + … +d[1];
因此,A[i]是其差分数组d[n]的前缀和d[1] + d[2] + … + d[i].
若我们不对原数组A[n]建立树状数组,而是对差分数组d[n]建立树状数组,则:
query(i)变成了单点查询 -> 查询num[i]的值;getSum(le,ri)对于原数组而言已经失去意义;add(i,x)除了初始化树状数组,对于原数组而言已经失去意义;
于是操作2可以通过差分数组建立的树状数组的query(i)实现,操作1呢?
操作1可以通过一个巧妙的方法实现,如下:
虽然我们并没有去更新原数组的值,但是通过bit[n]还原原数组(query(i)操作),我们已经达到了让对原数组区间加上/减去k的效果,这就实现了操作1.可以对这个方法总结如下:
存在原数组num[n],差分数组div[n],以差分数组建立的树状数组bit[n],则:
使i ∈ \in ∈[le,ri],(0 < le <= ri < n)的每一个num[i]同时+k,令bit[le] += k,bit[ri+1] -= k即可.
原理:前缀和的叠加作用.+k之后的(含)下标都受到+k的影响,-k之后的(含)下标都受到-k的影响,二者抵消,因此只有区间[le,ri]受到+k的作用.区间减去k同理,仔细想想就清楚了,很简单的.
上述操作实现如下:
int bit[100005],num[100005],div[100005],n;//num[]为原数组,div[]为num[]的差分数组,bit[]为树状数组;
int lowbit(int x) {
return x & -x;
}
int query(int i) { //单点查询,查询num[i];
int sum = 0;
while(i > 0) {
sum += bit[i];
i -= lowbit(i);
}
return sum;
}
void modify(int le,int ri,int x) { //区间修改,num[le,ri]都加上x;
if(le <= 0 || le > ri) return; //若要减去x,则传参传-x即可;
bit[le] += x;
if(ri < n) bit[ri+1] -= x;
}
void add(int i,int x) { //将div[i]的值加上x;
while(i <= n) { //除了初始化以外没有太大意义;
bit[i] += x;
i += lowbit(i);
}
}
int main() { //区间修改,单点查询 --> 差分数组建立树状数组;
memset(bit,0,sizeof bit); //先将树状数组清空;
for(int i = 1; i <= n; i++)
cin>>num[i];
div[1] = num[1];
for(int i = 2; i <= n; i++) //建立差分数组;
div[i] = num[i] - num[i-1];
for(int i = 1; i <= n; i++)
add(i,div[i]);
return 0;
}
两种操作的时间复杂度之前都讨论过了,都是O(logn)级别,这里查询一个数都要浪费时间而不是直接使用原数组下标查询,是因为区间更新如果每次都更新原数组,虽然查询复杂度降到O(1),但区间更新浪费的时间就不划算了,因此查询O(logn)的复杂度其实是可接受的、甚至是优秀的.
另外还有二维的树状数组,原理也是一样的,只是简单地维数扩展,较为少见,为避免啰嗦,这里就不再展开了.