POJ2104区间第k小
题意,给你一个数字序列和一堆询问,问你[l~r]里第k小的数
线段树,呸,主席树的入门板题,但是我还是学了半天QAQ
先说个大暴力,对于每个询问区间,我们排序,然后找第k个数,emm,复杂度爆表
然后貌似线段树可行??脑补一下,对于每个询问建一棵树,emm,貌似比暴力复杂度还高??
欸,所以我们引入了主席树,主席树呢,用到了前缀和的思路,我们通过前缀和sum[l~r]=sum[1~r]-sum[1~l-1]可以获得一些灵感,求区间第k小也可以这么做
/*下面开始引用
/*假设我们知道[1, l-1]之间有多少个数比第k小的数小,那么我们只要减去这些数之后在[1, r]区间内第k小的数即是[l, r]区间内的第k小数
更确切的说,我们要求[l, r]区间内的第k小数 可以 用以[1, r]建立的线段树去减去以[1, l-1] 建立的线段树
这样能够减的条件是这两棵树必须是同构的。
若是不太明白, 我们来举个例子:
如有序列 1 2 5 1 3 2 2 5 1 2
我们要求 [5,10]第5小的数
(数列中不存在4、6、7、8 但根据原理就都写出来了,为方便理解,去掉了hash的步骤,实际的代码中其实只要一棵4个叶子节点的树即可)
(红色的为个数)
我们建立的[1, l-1] (也就是[1, 4])之间的树为*/
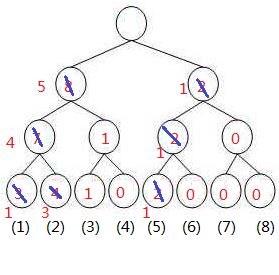
[1, r]也就是[1, 10]的树为
两树相减得到
/*我们来找第5小的数:
发现左子树为5 所以第5小的数在左边, 再往下(左4右1) 发现左边小于5了 ,所以第5小的数在右边 所以第5小的数就是3了
同样的,我们只要建立[1, i] (i是1到n之间的所有值)的所有树,每当询问[l, r]的时候,只要用[1, r]的树减去[1, l-1]的树,再找第k小就好啦
我们将这n个树看成是建立在一个大的线段树里的,也就是这个线段树的每个节点都是一个线段树( ——这就是主席树)
最初所有的树都是空树,我们并不需要建立n个空树,只要建立一个空树,也就是不必每个节点都建立一个空树
插入元素时,我们不去修改任何的结点,而是返回一个新的树( ——这就是函数式线段树)
因为每个节点都不会被修改,所以可以不断的重复用,因此插入操作的复杂度为O(logn)
总的复杂度为O((n+m)lognlogN) (听说 主席树的芭比说 加上垃圾回收, 可以减少一个log~~~ 然而这只是听说)*/引用完毕 原文
代码
//By AcerMo#include
#include
#include
#include
#include
using namespace std;
const int M=2000500;
int n,m,cnt;
int now[M],root[M];//离散化后的位置,树的根
struct Segt
{
int bo[2];
int sum;
Segt(){sum=0;}
}t[M];//线段树
struct past
{
int val,id;
}num[M];//存储数列
bool cmp(past a,past b)
{
return a.val>1;
if (val<=mid) update(val,t[rt].bo[0],l,mid);//然后考虑放到哪里
else update(val,t[rt].bo[1],mid+1,r);
return ;
}//构树
int query(int x,int y,int k,int l,int r)
{
int d=t[t[y].bo[0]].sum-t[t[x].bo[0]].sum;
if (l==r) return l;
int mid=(l+r)>>1;
if (k<=d) return query(t[x].bo[0],t[y].bo[0],k,l,mid);
else return query(t[x].bo[1],t[y].bo[1],k-d,mid+1,r);
}//按照刚刚的公式
int main()
{
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++)
scanf("%d",&num[i].val),num[i].id=i;
sort(num+1,num+n+1,cmp);
for (int i=1;i<=n;i++)
now[num[i].id]=i;
constt();
for (int i=1;i<=n;i++)
{
root[i]=root[i-1];
update(now[i],root[i],1,n);
}//构树
int l,r,kth;
for (int i=1;i<=m;i++)
{
scanf("%d%d%d",&l,&r,&kth);
int ans=num[query(root[l-1],root[r],kth,1,n)].val;//公式
printf("%d\n",ans);
}
return 0;
}