Android 动画-贝塞尔曲线

这次来梳理一下贝塞尔曲线的用法。说道贝塞尔曲线，应该想到的是自定义view，确实自定义view是绘制贝塞尔曲线的基础，绘制使用好贝塞尔曲线带来的交互效果，其实也是挺让人着迷的。这也是为何想把贝塞尔曲线归属到Android动画里的原因。

一、简介

什么是贝塞尔曲线

贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。主要结构：起始点、终止点（也称锚点）、控制点。通过调整控制点，贝塞尔曲线的形状会发生变化。

贝塞尔曲线的分类

• 一阶贝塞尔曲线(线段)

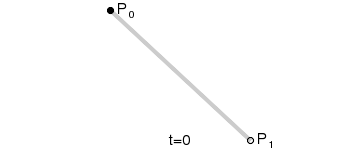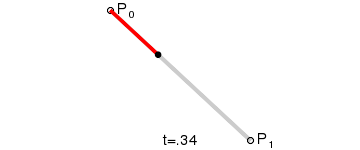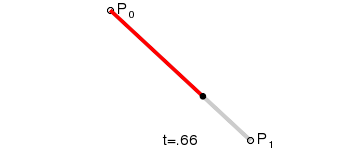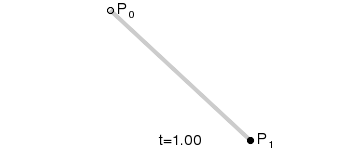
由 P0 至 P1 的连续点， 描述的一条线段。
代码示例：

@Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        canvas.drawLine(startX,startY,stopX,stopY,paint);
    }

• 二阶贝塞尔曲线(抛物线)

由 P0 至 P1 的连续点 Q0，描述一条线段。
由 P1 至 P2 的连续点 Q1，描述一条线段。
由 Q0 至 Q1 的连续点 B(t)，描述一条二次贝塞尔曲线。
代码示例：

@Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        mPath.reset();
        mPath.moveTo(mPointF1.x, mPointF1.y);
        mPath.quadTo(mControl.x, mControl.y, mPointF2.x, mPointF2.y);
        mPath.lineTo(mPointF1.x, mPointF1.y);
        canvas.drawPath(mPath, mPaint);
    }

主要是Path的quadTo方法，前两个参数是控制点的XY坐标，后两个参数是结束点的XY坐标。

• 三阶贝塞尔曲线

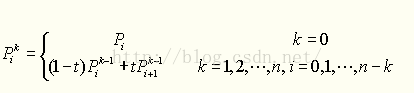
三阶贝塞尔由一点起始点一点结束点和两个控制点绘制的曲线。
对应Android Path的cubicTo方法。参数依次为控制点1的XY坐标，控制点2的XY坐标，结束点的XY坐标。
代码示例：

@Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        mPath.reset();
        mPath.moveTo(mPointF1.x, mPointF1.y);
        mPath.cubicTo(mControl.x, mControl.y,mControlTWo.x,mControlTWo.y, mPointF2.x, mPointF2.y);
        mPath.lineTo(mPointF1.x, mPointF1.y);
        canvas.drawPath(mPath, mPaint);
    }

贝塞尔曲线的基本介绍如上，发现对应在Android上的绘制方法是 android.graphics 的 Path里的方法。来看看Path的方法：

作用	相关方法	备注
移动起点	moveTo	移动下一次操作的起点位置
设置终点	setLastPoint	重置当前path中最后一个点位置，如果在绘制之前调用，效果和moveTo相同
连接直线	lineTo	添加上一个点到当前点之间的直线到Path
闭合路径	close	连接第一个点连接到最后一个点，形成一个闭合区域
添加内容	addRect, addRoundRect, addOval, addCircle, addPath, addArc, arcTo	添加(矩形， 圆角矩形， 椭圆， 圆， 路径， 圆弧) 到当前Path (注意addArc和arcTo的区别)
是否为空	isEmpty	判断Path是否为空
是否为矩形	isRect	判断path是否是一个矩形
贝塞尔曲线	quadTo, cubicTo	分别为二次和三次贝塞尔曲线的方法
rXxx方法	rMoveTo, rLineTo, rQuadTo, rCubicTo	不带r的方法是基于原点的坐标系(偏移量)，rXxx方法是基于当前点坐标系(偏移量)
填充模式	setFillType, getFillType, isInverseFillType, toggleInverseFillType	设置,获取,判断和切换填充模式
提示方法	incReserve	提示Path还有多少个点等待加入(这个方法貌似会让Path优化存储结构)
布尔操作(API19)	op	对两个Path进行布尔运算(即取交集、并集等操作)
计算边界	computeBounds	计算Path的边界
重置路径	reset, rewind	清除Path中的内容(reset相当于重置到new Path阶段，rewind会保留Path的数据结构)
矩阵操作	transform	矩阵变换

二、应用

1. 波浪效果
   
   如上图，一个简单的波浪效果，主要用到quadTo 和 ValueAnimator 的操作。

@Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        mPath.reset();
        mPath.moveTo(mLeft1.x, mLeft1.y);
        mPath.quadTo(mControlLeft1.x, mControlLeft1.y, mLeft2.x, mLeft2.y);
        mPath.quadTo(mControlLeft2.x, mControlLeft2.y, mFirst.x, mFirst.y);
        mPath.quadTo(mControlFirst.x, mControlFirst.y, mSecond.x, mSecond.y);
        mPath.quadTo(mControlSecond.x, mControlSecond.y, mRight.x, mRight.y);
        mPath.lineTo(mRight.x, mHeight);
        mPath.lineTo(mLeft1.x, mHeight);
        mPath.lineTo(mLeft1.x, mLeft1.y);
        canvas.drawPath(mPath, mPaint);
    }

private void startAnim() {
        ValueAnimator valueAnimator = ValueAnimator.ofFloat(mStart.x, 0);
        valueAnimator.setInterpolator(new LinearInterpolator());
        valueAnimator.setDuration(2000);
        valueAnimator.setRepeatCount(Animation.INFINITE);//动画效果重复
        valueAnimator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
            @Override
            public void onAnimationUpdate(ValueAnimator animation) {
                mLeft1.x = (float) animation.getAnimatedValue();
                mLeft2 = new PointF(mLeft1.x + mWidth / 2f, mHeight - mWaveHeight);
                mFirst = new PointF(mLeft2.x + mWidth / 2f, mHeight - mWaveHeight);
                mSecond = new PointF(mFirst.x + mWidth / 2f, mHeight - mWaveHeight);
                mRight = new PointF(mSecond.x + mWidth / 2f, mHeight - mWaveHeight);
                mControlLeft1 = new PointF(mLeft1.x + mWidth / 4f, mLeft1.y + mWavePeak);
                mControlLeft2 = new PointF(mLeft2.x + mWidth / 4f, mLeft2.y - mWaveTrough);
                mControlFirst = new PointF(mFirst.x + mWidth / 4f, mFirst.y + mWavePeak);
                mControlSecond = new PointF(mSecond.x + mWidth / 4f, mSecond.y - mWaveTrough);
                invalidate();
            }
        });
        valueAnimator.start();
    }