【Unity编程】Unity中关于四元数的API详解

Unity中关于四元数的API详解

Quaternion类

Quaternion（四元数）用于计算Unity旋转。它们计算紧凑高效，不受万向节锁的困扰，并且可以很方便快速地进行球面插值。 Unity内部使用四元数来表示所有的旋转。

Quaternion是基于复数，并不容易直观地理解。 不过你几乎不需要访问或修改单个四元数参数（x，y，z，w）; 大多数情况下，你只需要获取和使用现有的旋转（例如来自“Transform”），或者用四元数来构造新的旋转（例如，在两次旋转之间平滑插入）。
大部分情况下，你可能会使用到这些函数：

• Quaternion.LookRotation，
• Quaternion.Angle
• Quaternion.Euler
• Quaternion.Slerp
• Quaternion.FromToRotation
• Quaternion.identity。

Quaternion 是一个结构体，本身成员变量相对简单，可以作为函数参数高效传递。

Unity默认方向

在深入了解API之前，我们需要先明确一些基本的概念，就是方向、旋转究竟是如何表示的。
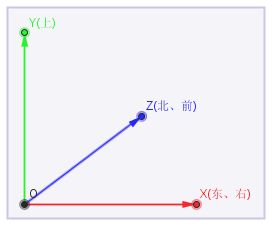
Unity中使用左手坐标系，假如把世界坐标系跟东南西北进行结合起来看，大致如下图所示：

默认的方向对应如下表：

坐标轴	对应方向
+x	右(东)
-x	左(西)
+y	上
-y	下
+Z	前(北)
-Z	后(南)

假设以你自己身体为例，你站立在地面上，面朝北方，此时就是默认方向，也就是Unity中的方向就是面向+Z轴方向，那么此时+X轴在东方，+Y轴对应正上方。此时对应的欧拉角是(0,0,0),此时对应的前方矢量是(0,0,1)，上方矢量是(0,1,0)。

这里我区分了左右上下前后的概念，因为这些概念同时也对应了Vector3类、Transform类中的相应的方向函数。

方向的表示法

①欧拉角表示法

假如你使用一组欧拉角表示旋转,XYZ三个参数代表相应轴向按照顺归YZX的旋转，因此(0、90、90)代表先进行+Z轴旋转90度，再沿着+Y轴进行90度旋转，更多详细内容可以参考前述文章《【Unity编程】Unity中的欧拉旋转》。

②前方上方矢量界定法

编程过程中，大部分需要明确指定方位的时候就需要使用这个方法。要确定一个朝向，我们可以使用两个向量来确定：即前方矢量和上方矢量。当一个朝向的前方和上方确定之后，这个朝向也就完全确定了。
举例来说，如果现在只提供一个朝向，就是你现在面朝北方，那么这个方向已经完全确定了吗？显然没有。因为你右侧躺在地上，看向北方，还是在面朝北方，这时候就需要另外一个矢量，也就是上方。当给出上方之后，这个朝向就完全确定了。

上方需要严格给出吗？

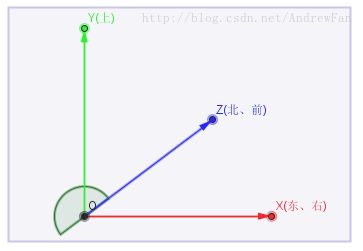
在Unity中，我们很多时候，不需要给出严格的上方朝向。比如，仍然是上面那个例子，如果我面朝北方，先给出(0,0,1)代表我的前方矢量。那么，如果我给出的方向不是严格的上方矢量，比如是(0,0.5,0.5)，是否可以？答案也是可以的，因为这两个矢量显然已经确定了一个方向，前方是严格的，而实际的上方可以通过前方朝着你给出的上方矢量旋转90度得出。也就是说，你给(0,1,0)作为上方矢量，和给出在下图中弧度范围内(不包含+Z和-Z)所有方向的矢量都是相同的结果。

③绕轴旋转界定法

第三种定义旋转的方法就是围绕某个指定的轴向旋转一定的角度。这个方法也可以确定一个相对旋转，它以从默认方向(此时前方+Z，上方+Y)出发，沿着指定的轴向进行指定角度的旋转，旋转后的前方和上方是确定的。因此这个方法也可以用来确定朝向。

④A向到B向相对旋转表示法

还有一种方法就是从A向到B向的相对旋转，这种表示了一个旋转的相对变化。比如A为(0,1,0)，B为(0,0,1)，也就是相对旋转量代表原来的上方被旋转到了前方，这样的一个四元数也可以用欧拉角表示成(90,0,0)，也就是沿着+X轴旋转了90度。

注意上面四中表示方法中，有的明确表明了上方矢量，有的好像只明确了前方矢量，要明确的一点就是，它们都是从默认矢量出发的，如果没有明确指定上方朝向，那么就是使用默认的上方，也就是+Y方向。

成员变量

• eulerAngles 欧拉角，返回当前四元数所对应的欧拉角
• this[int] 可以使用类似数组和下标的形式从四元数中获取四个四元数参数
• x、y、z、w 分别代表x、y、z、w 参数，具体代表的内容可以参考前文《【Unity编程】四元数(Quaternion)与欧拉角》，你最好不要通过修改四个参数来改变四元数，除非你真的非常了解它们的含义。

静态成员

• identity 单位四元数，也就是默认的无旋转状态，此时与世界坐标相同，前方指向+Z，上方指向+Y

成员函数

函数形式	解释
void Set(float new_x, float new_y, float new_z, float new_w)	设置x、y、z、w 分量，与this[]功能相同
void SetFromToRotation(Vector3 fromDirection, Vector3 toDirection)	设置成静态函数FromToRotation的结果
void SetLookRotation(Vector3 view, Vector3 up = Vector3.up)	设置成静态函数LookRotation的结果
void ToAngleAxis(out float angle, out Vector3 axis)	设置成静态函数AngleAxis的结果

说明：成员函数几个set方法多用于将当前四元数设置成目标四元数，目标四元数的构建方法与对应名称的静态函数相同。

静态函数

函数形式	解释
static float Angle(Quaternion a, Quaternion b)	计算两个四元数前方矢量之间的夹角度数
static Quaternion AngleAxis(float angle, Vector3 axis)	构建一个四元数，它表示沿着一个轴旋转固定角度，即上述表示法③
static float Dot(Quaternion a, Quaternion b)	计算两个四元数之间的点积，返回一个标量，这个函数一般用不到，它的点积不代表什么具体的物理含义，具体定义方法见我的前述文章
static Quaternion Euler(float x, float y, float z)	构建一个四元数，它用欧拉旋转表示，即上述表示法①
static Quaternion FromToRotation(Vector3 fromDirection, Vector3 toDirection)	构建一个四元数，它表示从指向fromDirection方向到指向toDirection方向的相对旋转量，见上述表示法④
static Quaternion Inverse(Quaternion rotation)	构建一个四元数，它是指定的四元数的逆，也就是逆向旋转，比如原四元数表示相对+X轴旋转了90度，那么此函数结果就是相对+X轴旋转了-90度
static Quaternion Lerp(Quaternion a, Quaternion b, float t)	构建一个四元数，表示从四元数a到b的球面插值，所谓的插值也就是中间旋转量，从a作为起点，此时对应t为0，到b为终点，此时对应t为1。当t取0-1之间的小数时，就代表了中间的插值结果。这个方法与Slerp相同，计算速度快，但是精度低，如果相对旋转变化量很小，则效果不理想
static Quaternion LerpUnclamped(Quaternion a, Quaternion b, float t)	与Lerp相同，区别是，Lerp的t值会被钳制在[0,1]之间，而此方法则不会，t允许超出计算
static Quaternion LookRotation(Vector3 forward, Vector3 upwards = Vector3.up)	构建一个四元数，使用前方上方矢量确定朝向，也就是上述表示法②
static Quaternion RotateTowards(Quaternion from, Quaternion to, float maxDegreesDelta)	构建一个四元数，表示从一个四元数from(的前方)向着另外一个四元数(的前方)旋转，但不能超出指定的角度，也就是如果两个前方矢量夹角超过指定角度，则旋转到达指定角度时就停止，若是夹角本身不足的话，则结果直接为目标四元数to，与上述表示法④的意思很接近
static Quaternion Slerp(Quaternion a, Quaternion b, float t)	球面插值，与Lerp功能相同，t值也被钳制，计算精度高，但是速度相对较慢
static Quaternion SlerpUnclamped(Quaternion a, Quaternion b, float t)	与Slerp功能相同，只是t值不被钳制，允许超出计算
static Quaternion operator * (Quaternion lhs, Quaternion rhs)	乘法运算符重载，当表示两个连续的旋转时，可以使用lhs * rhs的形式得出连续旋转的结果,lhs为左值，rhs为右值。注意左值是先进行的旋转，叠加右值旋转。用法示例:lhs = lhs * rhs;
static Vector3 operator *(Quaternion rotation, Vector3 point)	乘法运算符重载，表示对一个矢量point施加旋转rotation，得出旋转后的结果矢量。用法示例:Vector3 result=rotation * point

验证前方上方矢量表示法

为了验证前方上方矢量表示法的实际上方会重新计算，我设计了以下小实验。

在场景中设置三个物体，它们的朝向是打乱的，从左到右分别对应1、2、3。可以使用以下代码将三个物体朝向调整为一致。

        //前方上方矢量界定法的实际上方会重新计算
        m_t1.transform.rotation = Quaternion.LookRotation(Vector3.forward, Vector3.up);
        m_t2.transform.rotation = Quaternion.LookRotation(Vector3.forward, new Vector3(0,0.5f,-0.5f));
        m_t3.transform.rotation = Quaternion.LookRotation(Vector3.forward, new Vector3(0,0.5f,0.5f));

在start方法中执行上述代码后，如下：

三个物体朝向是一致的，也就说明了上方矢量确实是进行了重新计算。

总结几种表示方法

下面使用代码总结几种表示法，对应同样的四元数，大致有四种表示方法。

        //旋转量的4种表示形式

        Quaternion q1=Quaternion.Euler(90, 0, 0);
        Quaternion q2 = Quaternion.LookRotation(Vector3.down ,Vector3.forward);
        Quaternion q3 = Quaternion.AngleAxis(90,Vector3.right);
        Quaternion q4 = Quaternion.FromToRotation(Vector3.up, Vector3.forward);
        showQ("q1",q1);
        showQ("q2",q2);
        showQ("q3",q3);
        showQ("q4",q4);

它们的输出结果是：

也就是说，这几种形式表示的四元数结果完全相同。

将四元数旋转应用于子弹射击示例

当枪管转动起来，子弹仍然沿着正确的朝向发射出去，可以使用很简单的几句话，修改之前的代码后如下：

            Bullet_2 bullet = m_compPool.takeUnit();
            //发射时，将子弹的初始位置为枪口的当前位置
            bullet.m_transform.position = m_transform.position;
            //将子弹的初始化旋转设置为指向当前枪口前方
            bullet.m_transform.rotation = Quaternion.LookRotation(m_transform.forward);

---

本节代码可点此下载。觉得有用你就点个赞。