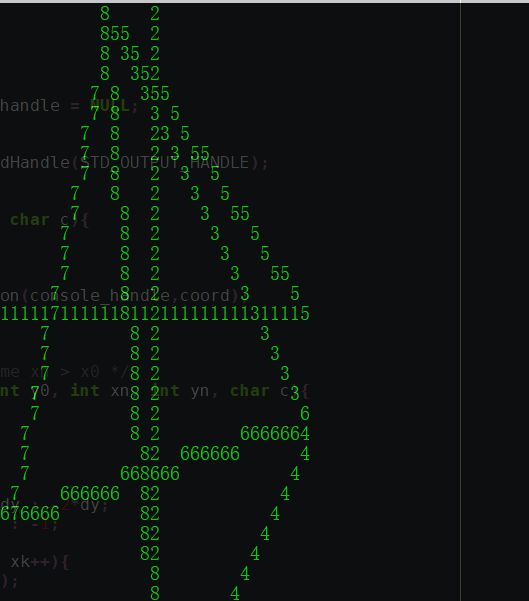
Bresenham画线算法的简单解释

网上其他资料感觉是简单问题复杂化，用实数的有理数（整数之比）表达方式分析更直接些。

为简化分析假设两端点为(x0,y0),(xn,yn),且满足

0<=x0= yn-y0.

令dy=yn-y0,dx=xn-x0.

则通过两端点的直线方程为

y=dy/dx * (x-x0)+y0

第k个点(x_k=x0+k,y_k)满足

y_k = dy/dx*k+y0,

y_k+1 = y_k+dy/dx.

对正实数r记r = [r]+(r)，当中[r]为整数，(r)为小数部分且-1/2 <= (r) <= 1/2, 相当于[r]为r的四舍五入结果。这里两边也可能是严格的小于号，但不影响分析。()与[]为运算符而不是通常意义下的括号。则所要绘制的点的坐标为(x_k,[y_k])。

y_k = [y_k] + (y_k)

y_k+1 = [y_k]+(y_k)+dy/dx

注意到这里x0,xn,y0,yn,dy,dx都是非负整数，当中dx>0.由于y_0=y0为整数，其小数部分(y_0)=0,(y_k)每次累加一个dy/dx或减去一个整数,因此(y_k)可以表示为

(y_k)=M/dx=2*M/(2*dx)=N/(2*dx)

这里N=2*M，M,N为整数。代入上式有

y_k+1 = [y_k] + (N+2*dy)/(2*dx)

因此只要N+2*dy>dx就说明[y_k]后面的一项大于0.5，[y_k+1]=[y_k]+1,并且N要减去2*dx使之保持在[-dx,dx]的区间内。否则[y_k+1]=y[k].

若xn=x0或yn=y0可单独处理，若abs(yn-y0)>abs(xn-x0)则只需将上面的dx,dy互换。剩下的就是细节问题，例如若x0>xn则需互换两点坐标或代码里增加判断保证dx>0，但若dy<0仍有问题，一是这里的N是通过大于正数dx判断[y_k]变化的，而dy为负数，累加后N恒为负数，同时[y_k+1]也不是[y_k]+1而是[y_k]-1。

公式中会出现负数，所以必须使用带符号类型正数，另外N虽然承担累加的任务，但它始终控制在[-dx,dx]的区间内，因此对一般的显示设备int16_t其实就够了。

为避免库依赖（偷懒）选择了wincon.h实现控制台光标定位，所以代码是不可移植的 。

#include 
#include 
#include 
#include 


	static HANDLE console_handle = NULL;
	
void plot_init(void){
	console_handle = GetStdHandle(STD_OUTPUT_HANDLE);
}
	
void plot_dot(int x,int y, char c){	
	COORD coord;
	coord.X = x;
	coord.Y = y;
	SetConsoleCursorPosition(console_handle,coord);
	putchar(c);
}

/* abs(dy) < abs(dx), assume xn > x0 */
void bresenham_x(int x0, int y0, int xn, int yn, char c){
	int dx = xn - x0;
	int dy = yn - y0;
	int N = 2*dy - dx;
	int yk = y0; 
	int xk;
	int Ninc = dy > 0 ? 2*dy : -2*dy;
	int ykinc = dy > 0 ? 1 : -1;

	for(xk = x0; xk <= xn; xk++){
		plot_dot(xk, yk, c);
		if(N > 0){
			yk = yk + ykinc;
			N = N - 2*dx;
		}
		N = N + Ninc;
	}
}

/* abs(dx) < abs(dy), assume yn > y0 */
void bresenham_y(int x0, int y0, int xn, int yn, char c){
	int dx = xn - x0;
	int dy = yn - y0;
	int N = 2*dx - dy;
	int xk = x0; 
	int yk;
	int Ninc = dx > 0 ? 2*dx : -2*dx;
	int xkinc = dx > 0 ? 1 : -1;	

	for(yk = y0; yk <= yn; yk++){
		plot_dot(xk, yk, c);
		if(N > 0){
			xk = xk + xkinc;
			N = N - 2*dy;
		}
		N = N + Ninc;
	}
}

void plot_line(int x0, int y0, int xn, int yn, char c){
	int xk;
	int yk;
	int dx = xn - x0;
	int dy = yn - y0;
	int adx = dx > 0 ? dx : -dx;
	int ady = dy > 0 ? dy : -dy;

	if(dx == 0){
		if(dy > 0){
			for(yk = y0; yk <= yn; yk++){
				plot_dot(x0,yk,c);
			}
		}
		else {
			for(yk = yn; yk <= y0; yk++){
				plot_dot(x0,yk,c);
			}
		}
		return ;
	} 
	if(dy == 0){
		if(dx > 0){
			for(xk = x0; xk <= xn; xk++){
				plot_dot(xk,y0,c);
			}
		}
		else {
			for(xk = xn; xk <= x0; xk++){
				plot_dot(xk,y0,c);
			}
		}
		return ;
	}
	if(ady < adx){
		if(xn > x0){
			bresenham_x(x0,y0,xn,yn,c);
		}
		else {
			bresenham_x(xn,yn,x0,y0,c);
		}
	}
	else {
		if(yn > y0){
			bresenham_y(x0,y0,xn,yn,c);
		}
		else {
			bresenham_y(xn,yn,x0,y0,c);
		}
	}
	
}



int main(int argc, char* argv[]){
 
	plot_init();
	
	plot_line(0,15,30,15,'1');
	plot_line(15,0,15,30,'2');
	plot_line(10,0,30,20,'3');
	plot_line(30,20,0,50,'4');
	plot_line(10,0,30,15,'5');
	plot_line(30,20,0,25,'6');
	plot_line(0,25,10,0,'7');
	plot_line(15,30,10,0,'8');
	
	return 0;
}