Splay bzoj3223文艺平衡树

Splay，中文名伸展树，是由tarjan大神发明的… orz
本质上就是BST加上splay操作——把结点x旋转到指定结点的下面。
每次查询完都把查到的数旋转到根，就可以让所有查找的时间效率为均摊O(logN) (不知道为啥…大佬说是就是吧orz)

因为Splay可以通过伸展操作随意改变树的结构，只要把排名L-1的结点伸展到根，把排名R+1的结点伸展到根的右孩子，R+1结点的左子树就包含了区间[L,R]中所有的点，所以Splay做区间操作非常方便。

缺点大概就是大得惊人的常数吧。

Splay的定义:

int ch[maxn][2], fa[maxn], val[maxn], siz[maxn], lazy[maxn];
int tot,root;
#define ls ch[now][0]
#define rs ch[now][1]

跟Treap的定义基本一样的，少个优先级，多个fa数组记录该结点的父亲。lazy是题目要用的翻转标记。
宏是用来偷懒的~

为什么Treap不要fa，Splay要？
因为Splay操作要用到父亲的父亲，不记录fa不会写。

旋转rotate:
跟所有平衡树的旋转都是一样的。get函数用来判断该结点是它父亲的哪个儿子。因为要维护区间，有些地方要pushup(把x旋转到y的上面之后，y的子树大小要重新计算)
贴张丑图以供想象

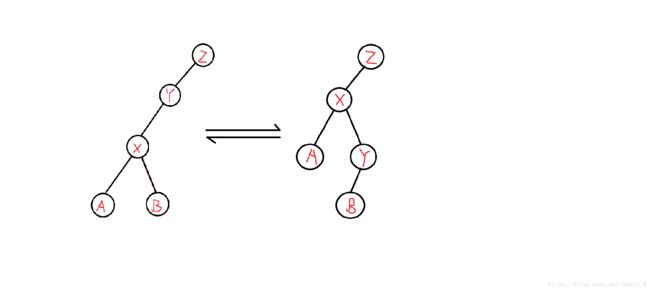
bool get(int x)//返回x是它父亲的哪个儿子
{
    return x == ch[fa[x]][1];
}

void connect(int son,int f,int dir)
{
    fa[son] = f;
    ch[f][dir] = son;
}

int y,z,yson,zson,xson;
void Rotate(int x)//把x旋转到fa[x]的位置,用get来判断要左旋还是右旋
{
    y = fa[x];
    z = fa[y];
    yson = get(x), zson = get(y);//记录x和y是他们父亲的哪个儿子
    xson = ch[x][yson^1];
    connect(x,z,zson);
    connect(y,x,yson^1);
    connect(xson,y,yson);
    pushup(y);
}

伸展splay——把x旋转到to的下面，成为to的儿子
三种情况:
1.fa[fa[x]] == to
往上旋一次即可
2.get(x) == get(fa[x])
设y是x的父亲，z是y的父亲，这种情况下，xyz是共线的（自行脑补）
tarjan大佬说这种情况要先把y旋上去，再把x旋上去
3.其他情况
x往上旋两次

void splay(int x,int to)//把x旋转到to的下面
{
    pushdown(x);//旋转后会改变结点关系，先下推标记！
    while(fa[x] != to)
    {
        if(fa[fa[x]] == to)
            Rotate(x);
        else if(get(x)==get(fa[x]))
            Rotate(fa[x]), Rotate(x);
        else
            Rotate(x), Rotate(x);
    }
    pushup(x);//旋转后会子树大小会变，更新
    if(to == 0)//x移到根了，更新根
        root = x;
}

建树build:
跟线段树差不多，多传一个参数f用来维护fa数组

void build(int l,int r,int &now,int f)
{
    if(l>r) return ;
    int m = l + r >> 1;
    newnode(m,now,f);
    build(l,m-1,ls,now);
    build(m+1,r,rs,now);
    pushup(now);
}

更新update(本题的更新是翻转)
首先把 L-1 splay到root，把 R+1 splay到root下面
build前要插入两个虚结点0和N+1，不然splay操作会越界

    newnode(0,root,0);
    newnode(N+1,ch[root][1],root);
    build(1,N,ch[ch[root][1]][0],ch[root][1]);

但splay函数是把下标为x的结点旋转到下标的to的结点下面，这里的结点编号跟要维护的区间的下标是不一致的
区间就是BST的中序序列，写个find函数把区间下标对应的结点编号求出来

int findk(int k,int now)//找区间中第k个数字的下标(0是第一个)
{
    pushdown(now);//往下找之前要pushdown(可能左右子树需要翻转)
    if(k == siz[ls]+1) return now;
    else if(k <= siz[ls]) return findk(k,ls);
    else return findk(k-siz[ls]-1,rs);
}

上面也提到了，0是区间中的第一个数字，所以要splay的是L和R+2

void update(int L,int R)
{
    int &now = root;//为了用上面那个宏弄了个引用...(一开始没写引用狂T o(╥﹏╥)o)
    splay(findk(L,root),0);
    splay(findk(R+2,root),root);
    lazy[ch[rs][0]] ^= 1;
    pushup(rs);
    pushup(root);
}

完整代码

#include
#include
using namespace std;

const int maxn = 1e5 + 5;
int ch[maxn][2], fa[maxn], val[maxn], siz[maxn], lazy[maxn];
int tot,root;
#define ls ch[now][0]
#define rs ch[now][1]
int N,M;
void newnode(int v,int &x,int f)
{
    x = ++tot;
    ch[x][0] = ch[x][1] = 0;
    val[x] = v;
    siz[x] = 1;
    lazy[x] = 0;
    fa[x] = f;
}

bool get(int x)//返回x是它父亲的哪个儿子
{
    return x == ch[fa[x]][1];
}

void pushup(int now)
{
    if(now)
        siz[now] = siz[ls] + siz[rs] + 1;
}

void pushdown(int now)
{
    if(lazy[now])
    {
        lazy[ls] ^= 1;
        lazy[rs] ^= 1;
        swap(ls,rs);//翻转把左右子树交换一下就好了
        lazy[now] = 0;
    }
}

void connect(int son,int f,int dir)
{
    fa[son] = f;
    ch[f][dir] = son;
}

int y,z,yson,zson,xson;
void Rotate(int x)//把x旋转到fa[x]的位置,用get来判断要左旋还是右旋
{
    y = fa[x];
    z = fa[y];
    yson = get(x), zson = get(y);//记录x和y是他们父亲的哪个儿子
    xson = ch[x][yson^1];
    connect(x,z,zson);
    connect(y,x,yson^1);
    connect(xson,y,yson);
    pushup(y);
}

void splay(int x,int to)//把x旋转到to的下面
{
    pushdown(x);
    while(fa[x] != to)
    {
        if(fa[fa[x]] == to)
            Rotate(x);
        else if(get(x)==get(fa[x]))
            Rotate(fa[x]), Rotate(x);
        else
            Rotate(x), Rotate(x);
    }
    pushup(x);
    if(to == 0)//x移到根了，更新根
        root = x;
}

void build(int l,int r,int &now,int f)
{
    if(l>r) return ;
    int m = l + r >> 1;
    newnode(m,now,f);
    build(l,m-1,ls,now);
    build(m+1,r,rs,now);
    pushup(now);
}

int findk(int k,int now)//找区间中第k个数字的下标(0是第一个)
{
    pushdown(now);
    if(k == siz[ls]+1) return now;
    else if(k <= siz[ls]) return findk(k,ls);
    else return findk(k-siz[ls]-1,rs);
}

void update(int L,int R)
{
    int &now = root;//为了用上面那个宏弄了个引用...(一开始没写引用狂T o(╥﹏╥)o)
    splay(findk(L,root),0);
    splay(findk(R+2,root),root);
    lazy[ch[rs][0]] ^= 1;
    pushup(rs);
    pushup(root);
}

void dfs(int now)
{
    pushdown(now);
    if(ls)
        dfs(ls);
    if(val[now]<=N&&val[now]>=1)
        printf("%d ",val[now]);
    if(rs)
        dfs(rs);
}

int main()
{
    int l,r;
    scanf("%d%d",&N,&M);
    newnode(0,root,0);
    newnode(N+1,ch[root][1],root);
    build(1,N,ch[ch[root][1]][0],ch[root][1]);
    while(M--)
    {
        scanf("%d%d",&l,&r);
        update(l,r);
    }
    dfs(root);
    return 0;
}