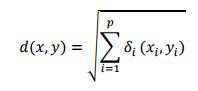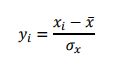评分卡模型开发--用户数据缺失值处理

原文链接： https://cloud.tencent.com/developer/article/1016341

转自：https://cloud.tencent.com/developer/article/1016341

在我们搜集样本时，许多样本中一般都含有缺失值，这种情况在现实问题中非常普遍，这会导致一些不能处理缺失值的分析方法无法应用，因此，在信用风险评级模型开发的第一步我们就要进行缺失值处理。缺失值处理的方法，包括如下几种。 （1） 直接删除含有缺失值的样本。 （2） 根据样本之间的相似性填补缺失值。 （3） 根据变量之间的相关关系填补缺失值。 直接删除含有缺失值的样本时最简单的方法，尤其是这些样本所占的比例非常小时，用这种方法就比较合理，但当缺失值样本比例较大时，这种缺失值处理方法误差就比较大了。在采用删除法剔除缺失值样本时，我们通常首先检查样本总体中缺失值的个数，在R中使用complete.cases()函数来统计缺失值的个数。

>GermanCredit[!complete.cases(GermanCredit),]
>nrow(GermanGredit[!complete.cases(GermanCredit),]
>GermanCredit<-na.omit(GermanCredit)    #删除包含缺失值的样本
>View(GermanCredit)                     #查看结果

根据样本之间的相似性填补缺失值是指用这些缺失值最可能的值来填补它们，通常使用能代表变量中心趋势的值进行填补，因为代表变量中心趋势的值反映了变量分布的最常见值。代表变量中心趋势的指标包括平均值、中位数、众数等，那么我们采用哪些指标来填补缺失值呢？最佳选择是由变量的分布来确定，例如，对于接近正态分布的变量来说，由于所有观测值都较好地聚集在平均值周围，因此平均值就就是填补该类变量缺失值的最佳选择。然而，对于偏态分布或者离群值来说，平均值就不是最佳选择。因为偏态分布的大部分值都聚集在变量分布的一侧，平均值不能作为最常见值的代表。对于偏态分布或者有离群值的分布而言，中位数是更好地代表数据中心趋势的指标。对于名义变量（表3.1中的定性指标），通常采用众数填补缺失值。 我们将上述分析放在一个统一的函数centralImputation()中，对于数值型变量，我们用中位数填补，对于名义变量，我们用众数填补，函数代码如下：

centralImputation<-function(data)
  {
  for(i in seq(ncol(data)))
     if(any(idx<-is.na(data[,i])))
     {
       data[idx,i]<-centralValue(data[,i])
       }
     data}
     centralValue<-function(x,ws=NULL)
     {
       if(is.numeric(x))
     {
         if(is.null(ws))
         {
           median(x,na.rm = T)
           }
       else if((s0)
       {
         sum(x*(ws/s))
         }
       else NA
         }
       else
       {
         x<-as.factor(x)
         if(is.null(ws))
         {
           levels(x)[which.max(table(x))]
           }
       else
       {
         levels(x)[which.max(aggregate(ws,list(x),sum)[,2])]
         }
       }
  }

调用上述函数对缺失值进行填补，代码如下：

x<-centralImputation(GermanCredit)
View(x)     #查看填补结果

上述按照中心趋势进行缺失值填补的方法，考虑的是数据每列的数值或字符属性，在进行缺失值填补时，我们也可以考虑每行的属性，即为我们要讲述的第三种处理缺失值的方法，根据变量之间的相关关系填补缺失值。 当我们采用数据集每行的属性进行缺失值填补时，通常有两种方法，第一种方法是计算k个（本文k=10）最相近样本的中位数并用这个中位数来填补缺失值，如果缺失值是名义变量，则使用这k个最近相似数据的加权平均值进行填补，权重大小随着距离待填补缺失值样本的距离增大而减小，本文我们采用高斯核函数从距离获得权重，即如果相邻样本距离待填补缺失值的样本的距离为d，则它的值在加权平均中的权重为：

在寻找跟包含缺失值的样本最近的k个邻居样本时，最常用的经典算法是knn(k-nearest-neighbor) 算法，它通过计算样本间的欧氏距离，来寻找距离包含缺失值样本最近的k个邻居，样本x和y之间欧式距离的计算公式如下：

式中：δ_i ( )是变量i的两个值之间的距离，即

在计算欧式距离时，为了消除变量间不同尺度的影响，通常要先对数值变量进行标准化，即：

我们将上述根据数据集每行的属性进行缺失值填补的方法，封装到knnImputation()函数中，代码如下：

knnImputation<-function(data,k=10,scale=T,meth="weighAvg",distData=NULL)
{
  n<-nrow(data)
  if(!is.null(distData))
  {
    distInit<-n+1
    data<-rbind(data,distData)
  }
  else
  {
    disInit<-1
  }
  N<-nrow(data)
  ncol<-ncol(data)
  nomAttrs<-rep(F,ncol)
  for(i in seq(ncol))
  {
    nomAttrs[i]<-is.factor(data[,1])
  }
  nomAttrs<-which(nomAttrs)
  hasNom<-length(nomAttrs)
  contAttrs<-setdiff(seq(ncol),nomAttrs)
  dm<-data
  if(scale)
  {
    dm[,contAttrs]<-scale(dm[,contAttrs])
  }
  if(hasNom)
  {
    for(i in nomAttrs)
      dm[,i]<-as.integer(dm[,i])
  }
  dm0,1,dist[,xnom])
    }
    dist<-dist[,-tgtAs]
    dist<-sqrt(drop(dist^2%*%rep(1,ncol(dist))))
    ks<-order(dist)[seq(k)]
    for(j in tgtAs) if(meth=="median")
    {
      data[i,j]<-centralValue(data[setdiff(distInit:N,nas),j][ks])
    }
    else
    {
      data[i,j]<-centralValue(data[setdiff(distInit:N,nas),j]
                              [ks],exp(-dist[ks]))
    }
  }
  data[1:n,]
}

调用knnImputation()函数，用knn方法填补缺失值，代码如下：

d<-knnImputation(GermanCredit)
View(d)     #查看填补结果

如果使用k近邻的中位数来填补缺失值，可使用如下代码：

d<-knnImputation(GermanCredit,k=10,meth=”median”)
View(d)

综上，我们共讲述了三种缺失值的处理方法，当我们决定采用哪种方法来填补缺失值时，通常需要根据所分析领域的具体情况来确定。 缺失值处理完毕后，我们还需要进行异常值处理。异常值是指明显偏离大多数抽样数据的数值，异常值处理见下篇： http://write.blog.csdn.net/mdeditor#!postId=76599792