cordic算法详解

作者：善良的一休君

来源：CSDN

原文：https://blog.csdn.net/qq_39210023/article/details/77456031

版权声明：本文为博主原创文章，转载请附上博文链接！

---------------------

       目前，学习与开发FPGA的程序员们大多使用的是Verilog HDL语言（以下简称为Verilog），关于Verilog的诸多优点一休哥就不多介绍了，在此，我们将重点放在Verilog的运算操作上。

我们都知道，在Verilog中，运算一般分为逻辑运算（与或非等）与算术运算（加减乘除等）。而在一开始学习Verilog时，老司机一定会提醒我们，“切记，千万别用‘/’除、‘%’取模（有的也叫取余）和‘**’幂。”这话说的不无道理，因为这三个运算是不可综合的。但，需清楚理解的是，不可综合的具体意思为不能综合为简单的模块，当我们在程序中调用了这些运算时，‘/’除和‘%’取模在Quartus软件中是可以综合的，因此可以正常调用运行，但是会消耗一些逻辑资源，而且会产生延时，即这两个运算的处理时间会很长，可能会大于时序控制时钟的单周期时间。此时呢，我们会建议你调用IP核来实现运算操作，虽然这样也会消耗许多逻辑资源，但产生的延时相对较小满足了你基本的需求。

问题好像迎刃而解了，可是仔细一想，除了这些运算，我们还剩下什么？对呀，三角函数，反三角函数，对数函数，指数函数呢，这些函数我们在高中就学习了的呀，难道在FPGA中就没有用武之地吗？有人会说，查找表呗，首先将某个运算的所有可能的输入与输出对一一罗列出来，然后放进Rom中，然后根据输入查表得到输出。这个方法虽然有效的避免了延时问题，却是一个十分消耗资源的方法，不适合资源紧张的设计。那么，就真的没有办法了吗？

答案就是咱们今天的标题了，CORDIC，而且CORDIC是一个比较全能的算法，通过这一原理，我们可以实现三角函数，反三角函数，对数函数，指数函数等多种运算。接下来，一休哥就带领大家来学习CORDIC的原理吧。（题外话：请相信一休哥，本文不会让你感到太多痛苦~）

本文将分三个小部分来展开介绍：

1、CORDIC的基本原理介绍

2、CORDIC的具体操作流程介绍

3、CORDIC的旋转模式——Verilog仿真

本文涉及到的全部资料链接：

链接：http://pan.baidu.com/s/1gfrJzMj 密码：x92u

 

一、CORDIC的基本原理介绍

CORDIC算法是一个“化繁为简”的算法，将许多复杂的运算转化为一种“仅需要移位和加法”的迭代操作。CORDIC算法有旋转和向量两个模式，分别可以在圆坐标系、线性坐标系和双曲线坐标系使用，从而可以演算出8种运算，而结合这8种运算也可以衍生出其他许多运算。下表展示了8种运算在CORDIC算法中实现的条件。

首先，我们先从旋转模式下的圆坐标系讲起，这也是CORDIC方法最初的用途。

 

1、CORDIC的几何原理介绍

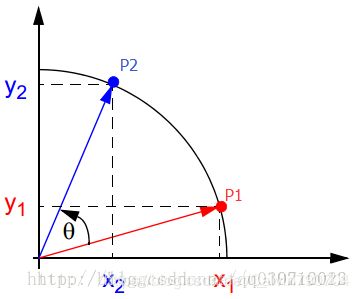
假设在xy坐标系中有一个点P1（x1，y1），将P1点绕原点旋转θ角后得到点P2（x2，y2）。

于是可以得到P1和P2的关系。

x2 = x1cosθ – y1sinθ = cosθ(x1 – y1tanθ)

y2 = y1cosθ + x1sinθ = cosθ(y1 +x1tanθ)

以上就是CORDIC的几何原理部分，而我们该如何深入理解这个几何原理的真正含义呢？

从原理中，我们可以知道，当已知一个点P1的坐标，并已知该点P1旋转的角度θ，则可以根据上述公式求得目标点P2的坐标。然后，麻烦来了，我们需要用FPGA去执行上述运算操作，而FPGA的Verilog语言根本不支持三角函数运算。因此，我们需要对上述式子进行简化操作，将复杂的运算操作转换为一种单一的“迭代位移”算法。那么，接下来我们介绍优化算法部分。

 

2、CORDIC的优化算法介绍

我们先介绍算法的优化原理：将旋转角θ细化成若干分固定大小的角度θi，并且规定θi满足tanθi = 2^(-i)，因此∑θi的值在[-99.7°，99.7°]范围内，如果旋转角θ超出此范围，则运用简单的三角运算操作即可（加减π）。

然后我们需要修改几何原理部分的假设，假设在xy坐标系中有一个点P0（x0，y0），将P0点绕原点旋转θ角后得到点Pn（xn，yn）。

于是可以得到P0和Pn的关系。

xn = x0cosθ – y0sinθ = cosθ(x0 – y0tanθ)

yn = y0cosθ + x0sinθ = cosθ(y0 + x0tanθ)

然后，我们将旋转角θ细化成θi，由于每次的旋转角度θi是固定不变的（因为满足tanθi = 2^(-i)），如果一直朝着一个方向旋转则∑θi一定会超过θ（如果θ在[-99.7°，99.7°]范围内）。因此我们需要对θi设定一个方向值di。如果旋转角已经大于θ，则di为-1，表示下次旋转为顺时针，即向θ靠近；如果旋转角已经小于θ，则di为1，表示下次旋转为逆时针，即也向θ靠近。然后我们可以得到每次旋转的角度值diθi，设角度剩余值为zi+1，则有zi+1 = zi - diθi，其中z0为θ。如此随着i的增大，角度剩余值zi+1将会趋近于0，此时运算结束。（注：可以发现，di与zi的符号位相同）

第一次旋转θ0，d0为旋转方向：

x1 = cosθ0(x0 – d0y0tanθ0)

y1 = cosθ0(y0 + d0x0tanθ0)

第二次旋转θ1，d1为旋转方向：

x2 = cosθ1(x1 – d1y1tanθ1) = cosθ1cosθ0(x0 – d0y0tanθ0 – d1y0tanθ1 – d1d0 x0tanθ1 tanθ0)

y2 = cosθ1(y1 + d1x1tanθ1) = cosθ1cosθ0(y0 + d0x0tanθ0 + d1x0tanθ1 – d1d0y0tanθ1 tanθ0)

大家可能已经发现了，在我们旋转的过程中，式子里一直会有tanθi和cosθi，而每次都可以提取出cosθi。虽然我们的FPGA无法计算tanθi，但我们知道tanθi = 2^(-i)，因此可以执行和tanθi效果相同的移位操作 2^(-i)来取代tanθi。而对于cosθi，我们可以事先全部提取出来，然后等待迭代结束之后（角度剩余值zi+1趋近于0，一般当系统设置最大迭代次数为16时zi+1已经很小了），然后计算出∏cosθi的值即可。

总结一下：

迭代公式有三：

xi+1 = xi – d iy i 2^(-i)，提取了cosθi， 2^(-i)等效替换了tanθi之后

yi+1 = yi + d ix i 2^(-i)，提取了cosθi， 2^(-i)等效替换了tanθi之后

zi+1 = zi - diθi

其中i从0开始迭代，假设当i = n-1时，zn趋近于0，迭代结束。然后对结果乘上∏cosθi（i从0至n-1），于是得到点Pn（xn∏cosθi，yn∏cosθi），此时的点Pn就近似等于之前假设中的点Pn（xn，yn）了，所以此时的点Pn同样满足之前假设得到的公式：

xn∏cosθi = x0cosθ – y0sinθ

yn∏cosθi = y0cosθ + x0sinθ

由于i从0至n-1，所以上式可以转化成下式：

xn = 1/∏cosθi(x0cosθ – y0sinθ)，（其中i从0至n-1）

yn = 1/∏cosθi(y0cosθ + x0sinθ)，（其中i从0至n-1）

注意：上式中的xn，yn是经过迭代后的结果，而不是之前假设中的点Pn（xn，yn）。了解这点是十分重要的。

根据高中学的三角函数关系，可以知道cosθi = 1/[(1+tan2θi)^0.5] = 1/[(1+2^(-2i))^0.5]，而1/[(1+2^(-2i))^0.5]的极值为1，因此我们可以得出一个结论：当i的次数很大时，∏cosθi的值趋于一个常数。

关于如何计算∏cosθi的代码如下所示：

close all;

clear;

clc;

% 初始化

die = 16;%迭代次数

jiao = zeros(die,1);%每次旋转的角度

cos_value = zeros(die,1);%每次旋转的角度的余弦值

K = zeros(die,1);%余弦值的N元乘积

K_1 = zeros(die,1);%余弦值的N元乘积的倒数

for i = 1 : die

    a = 2^(-(i-1));

    jiao(i) = atan(a);

    cos_value(i) = cos(jiao(i));

    if( i == 1)

        K(i) = cos_value(i);

        K_1(i) = 1/K(i);

    else

        K(i) = K(i-1)*cos_value(i);

        K_1(i) = 1/K(i);

    end

end

jiao = vpa(rad2deg(jiao)*256,10)

cos_value = vpa(cos_value,10)

K = vpa(K,10)

K_1 = vpa(K_1,10)

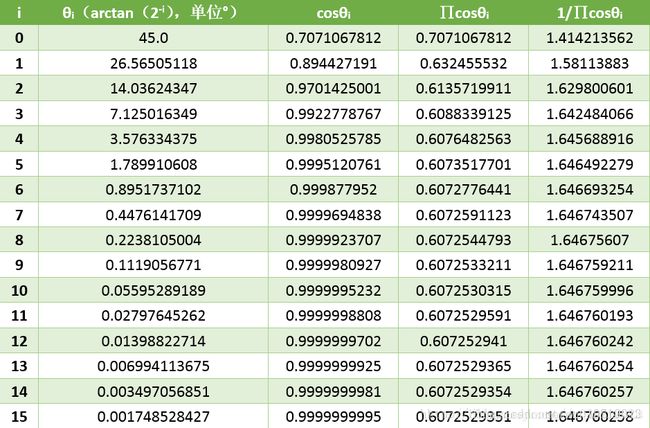
这里写图片描述

从上表也可以看出，当迭代次数为16，i=15时，cosθi的值已经非常趋近于1了，∏cosθi的值则约等于0.607253，1/∏cosθi为1.64676。所以当迭代次数等于16时，通过迭代得到的点Pn坐标已经非常接近之前假设中的点Pn。所以，当迭代次数等于16时，这个式子是成立的。

xn = 1/∏cosθi(x0cosθ – y0sinθ)，（其中i从0至n-1）

yn = 1/∏cosθi(y0cosθ + x0sinθ)，（其中i从0至n-1）

此时，已知条件有三个x0、y0和θ。通过16次迭代，我们可以得到xn和yn。而式中的∏cosθi是个随i变化的值，我们可以预先将其值存入系统中。

然后，我们人为设置x0 = ∏cosθi，y0 = 0，则根据等式，xn = cosθ，yn = sinθ。其中1/∏cosθi的值我们也同样预先存入系统中。如此，我们就实现了正弦和余弦操作了。

 

二、CORDIC的具体操作流程介绍

1、CORDIC的旋转模式

由于算法较复杂，一休哥再总结一些具体的操作流程。

1、 设置迭代次数为16，则x0 = 0.607253，y0 = 0，并输入待计算的角度θ，θ在[-99.7°，99.7°]范围内。

2、 根据三个迭代公式进行迭代，i从0至15：

xi+1 = xi – d iy i2-i

yi+1 = yi + d ix i2-i

zi+1 = zi - diθi

注：z0 = θ，di与zi同符号。

3、 经过16次迭代计算后，得到的x16 和y16分别为cosθ和sinθ。

至此，关于CORDIC的三角函数cosθ和sinθ的计算原理讲解结束。

关于CORDIC算法计算三角函数cosθ和sinθ的MATLAB代码如下所示：

 

close all;

clear;

clc;

% 初始化

die = 16;%迭代次数

x = zeros(die+1,1);

y = zeros(die+1,1);

z = zeros(die+1,1);

x(1) = 0.607253;%初始设置

z(1) = pi/4;%待求角度θ

%迭代操作

for i = 1:die

    if z(i) >= 0

        d = 1;

    else

        d = -1;

    end

    x(i+1) = x(i) - d*y(i)*(2^(-(i-1)));

    y(i+1) = y(i) + d*x(i)*(2^(-(i-1)));

    z(i+1) = z(i) - d*atan(2^(-(i-1)));

end

cosa = vpa(x(17),10)

sina = vpa(y(17),10)

c = vpa(z(17),10)

2、CORDIC的向量模式

讲完了旋转模式后，我们接着讲讲向量模式下的圆坐标系。

在这里，我们需从头来过了，假设在xy坐标系中有一个点P0（x0，y0），将P0点绕原点旋转θ角后得到点Pn（xn，0），θ在[-99.7°，99.7°]范围内。

于是可以得到P0和Pn的关系：

xn = x0cosθ – y0sinθ = cosθ(x0 – y0tanθ)

yn = y0cosθ + x0sinθ = cosθ(y0 + x0tanθ) = 0

如何得到Pn（xn，yn）一直是我们的目标。而此时，我们还是列出那几个等式：

根据三个迭代公式进行迭代，i从0至15：

xi+1 = xi – d iy i2-i

yi+1 = yi + d ix i2-i

zi+1 = zi - diθi

不过此时我们尝试改变初始条件：

设置迭代次数为16，则x0 = x，y0 = y，z0 = 0，di与yi的符号相反。表示，经过n次旋转，使Pn靠近x轴。

因此，当迭代结束之后，Pn将近似接近x轴，此时yn = 0，可知旋转了θ，即zn = θ = arctan(y/x)。

而

xn = 1/∏cosθi(x0cosθ – y0sinθ)，（其中i从0至n-1）

yn = 1/∏cosθi(y0cosθ + x0sinθ)，（其中i从0至n-1）

因此，可得ycosθ + xsinθ = 0，

xn = 1/∏cosθi(xcosθ – ysinθ) = 1/∏cosθi{ [ (xcosθ – ysinθ)^2]^(1/2)}

= 1/∏cosθi{ [ x2cos2θ + y2sin2θ – 2xysinθcosθ]^(1/2)}

= 1/∏cosθi{ [ x2cos2θ + y2sin2θ + y2 cos2θ + x2sin2θ]^(1/2)}

= 1/∏cosθi{ [ x2 + y2]^(1/2)}

由上可以知道，我们通过迭代，就算出了反正切函数zn = θ = arctan(y/x)，以及向量OP0（x，y）的长度 d = xn * ∏cosθi。

关于反正切函数，一休哥要多啰嗦几句了，由于θ在[-99.7°，99.7°]范围内，所以我们输入向量OP0（x，y）时，需要保证其在第一、四象限。

关于CORDIC算法计算反三角函数arctanθ的MATLAB代码如下所示：

 

close all;

clear;

clc;

% 初始化

die = 16;%迭代次数

x = zeros(die+1,1);

y = zeros(die+1,1);

z = zeros(die+1,1);

x(1) = 100;%初始设置

y(1) = 200;%初始设置

k = 0.607253;%初始设置

%迭代操作

for i = 1:die

    if y(i) >= 0

        d = -1;

    else

        d = 1;

    end

    x(i+1) = x(i) - d*y(i)*(2^(-(i-1)));

    y(i+1) = y(i) + d*x(i)*(2^(-(i-1)));

    z(i+1) = z(i) - d*atan(2^(-(i-1)));

end

d = vpa(x(17)*k,10)

a = vpa(y(17),10)

c = vpa(rad2deg(z(17)),10)

 

三、CORDIC的旋转模式——Verilog仿真

一休哥在编写CORDIC算法时，采用了16级流水线，仿真效果十分明显。以下是顶层文件的代码。

为了避免浮点运算，为了满足精度要求，一休哥对每个变量都放大了2^16倍，并且引入了有符号型reg和算术右移。

关于Verilog代码的编写，一休哥已经不想多说了，因为代码是完全符合我之前所讲的CORDIC的原理与MATLAB仿真代码。相信大家在看完本文的前两个部分之后，对Verilog的理解应该不是难事儿。

 

 

module Cordic_Test

(

    CLK_50M,RST_N,

    Phase,

    Sin,Cos,Error

);

 

input                       CLK_50M;

input                       RST_N;

input       [31:0]          Phase;

output      [31:0]          Sin;

output      [31:0]          Cos;

output      [31:0]          Error;

 

`define rot0  32'd2949120       //45度*2^16

`define rot1  32'd1740992       //26.5651度*2^16

`define rot2  32'd919872        //14.0362度*2^16

`define rot3  32'd466944        //7.1250度*2^16

`define rot4  32'd234368        //3.5763度*2^16

`define rot5  32'd117312        //1.7899度*2^16

`define rot6  32'd58688         //0.8952度*2^16

`define rot7  32'd29312         //0.4476度*2^16

`define rot8  32'd14656         //0.2238度*2^16

`define rot9  32'd7360          //0.1119度*2^16

`define rot10 32'd3648          //0.0560度*2^16

`define rot11 32'd1856          //0.0280度*2^16

`define rot12 32'd896           //0.0140度*2^16

`define rot13 32'd448           //0.0070度*2^16

`define rot14 32'd256           //0.0035度*2^16

`define rot15 32'd128           //0.0018度*2^16

 

parameter Pipeline = 16;

parameter K = 32'h09b74;    //K=0.607253*2^16,32'h09b74,

 

reg signed  [31:0]      Sin;

reg signed  [31:0]      Cos;

reg signed  [31:0]      Error;

reg signed  [31:0]      x0=0,y0=0,z0=0;

reg signed  [31:0]      x1=0,y1=0,z1=0;

reg signed  [31:0]      x2=0,y2=0,z2=0;

reg signed  [31:0]      x3=0,y3=0,z3=0;

reg signed  [31:0]      x4=0,y4=0,z4=0;

reg signed  [31:0]      x5=0,y5=0,z5=0;

reg signed  [31:0]      x6=0,y6=0,z6=0;

reg signed  [31:0]      x7=0,y7=0,z7=0;

reg signed  [31:0]      x8=0,y8=0,z8=0;

reg signed  [31:0]      x9=0,y9=0,z9=0;

reg signed  [31:0]      x10=0,y10=0,z10=0;

reg signed  [31:0]      x11=0,y11=0,z11=0;

reg signed  [31:0]      x12=0,y12=0,z12=0;

reg signed  [31:0]      x13=0,y13=0,z13=0;

reg signed  [31:0]      x14=0,y14=0,z14=0;

reg signed  [31:0]      x15=0,y15=0,z15=0;

reg signed  [31:0]      x16=0,y16=0,z16=0;

reg         [ 1:0]      Quadrant [Pipeline:0];

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x0 <= 1'b0;                        

        y0 <= 1'b0;

        z0 <= 1'b0;

    end

    else

    begin

        x0 <= K;

        y0 <= 32'd0;

        z0 <= Phase[15:0] << 16;

    end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x1 <= 1'b0;                        

        y1 <= 1'b0;

        z1 <= 1'b0;

    end

    else if(z0[31])

    begin

      x1 <= x0 + y0;

      y1 <= y0 - x0;

      z1 <= z0 + `rot0;

    end

    else

    begin

      x1 <= x0 - y0;

      y1 <= y0 + x0;

      z1 <= z0 - `rot0;

    end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x2 <= 1'b0;                        

        y2 <= 1'b0;

        z2 <= 1'b0;

    end

    else if(z1[31])

   begin

        x2 <= x1 + (y1 >>> 1);

        y2 <= y1 - (x1 >>> 1);

        z2 <= z1 + `rot1;

   end

   else

   begin

       x2 <= x1 - (y1 >>> 1);

       y2 <= y1 + (x1 >>> 1);

       z2 <= z1 - `rot1;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x3 <= 1'b0;                        

        y3 <= 1'b0;

        z3 <= 1'b0;

    end

    else if(z2[31])

   begin

       x3 <= x2 + (y2 >>> 2);

       y3 <= y2 - (x2 >>> 2);

       z3 <= z2 + `rot2;

   end

   else

   begin

       x3 <= x2 - (y2 >>> 2);

       y3 <= y2 + (x2 >>> 2);

       z3 <= z2 - `rot2;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x4 <= 1'b0;                         

        y4 <= 1'b0;

        z4 <= 1'b0;

    end

    else if(z3[31])

   begin

       x4 <= x3 + (y3 >>> 3);

       y4 <= y3 - (x3 >>> 3);

       z4 <= z3 + `rot3;

   end

   else

   begin

       x4 <= x3 - (y3 >>> 3);

       y4 <= y3 + (x3 >>> 3);

       z4 <= z3 - `rot3;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x5 <= 1'b0;                        

        y5 <= 1'b0;

        z5 <= 1'b0;

    end

    else if(z4[31])

   begin

       x5 <= x4 + (y4 >>> 4);

       y5 <= y4 - (x4 >>> 4);

       z5 <= z4 + `rot4;

   end

   else

   begin

       x5 <= x4 - (y4 >>> 4);

       y5 <= y4 + (x4 >>> 4);

       z5 <= z4 - `rot4;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x6 <= 1'b0;                        

        y6 <= 1'b0;

        z6 <= 1'b0;

    end

    else if(z5[31])

   begin

       x6 <= x5 + (y5 >>> 5);

       y6 <= y5 - (x5 >>> 5);

       z6 <= z5 + `rot5;

   end

   else

   begin

       x6 <= x5 - (y5 >>> 5);

       y6 <= y5 + (x5 >>> 5);

       z6 <= z5 - `rot5;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x7 <= 1'b0;                         

        y7 <= 1'b0;

        z7 <= 1'b0;

    end

    else if(z6[31])

   begin

       x7 <= x6 + (y6 >>> 6);

       y7 <= y6 - (x6 >>> 6);

       z7 <= z6 + `rot6;

   end

   else

   begin

       x7 <= x6 - (y6 >>> 6);

       y7 <= y6 + (x6 >>> 6);

       z7 <= z6 - `rot6;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x8 <= 1'b0;                        

        y8 <= 1'b0;

        z8 <= 1'b0;

    end

    else if(z7[31])

   begin

       x8 <= x7 + (y7 >>> 7);

       y8 <= y7 - (x7 >>> 7);

       z8 <= z7 + `rot7;

   end

   else

   begin

       x8 <= x7 - (y7 >>> 7);

       y8 <= y7 + (x7 >>> 7);

       z8 <= z7 - `rot7;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x9 <= 1'b0;                        

        y9 <= 1'b0;

        z9 <= 1'b0;

    end

    else if(z8[31])

   begin

       x9 <= x8 + (y8 >>> 8);

       y9 <= y8 - (x8 >>> 8);

       z9 <= z8 + `rot8;

   end

   else

   begin

       x9 <= x8 - (y8 >>> 8);

       y9 <= y8 + (x8 >>> 8);

       z9 <= z8 - `rot8;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x10 <= 1'b0;                       

        y10 <= 1'b0;

        z10 <= 1'b0;

    end

    else if(z9[31])

   begin

       x10 <= x9 + (y9 >>> 9);

       y10 <= y9 - (x9 >>> 9);

       z10 <= z9 + `rot9;

   end

   else

   begin

       x10 <= x9 - (y9 >>> 9);

       y10 <= y9 + (x9 >>> 9);

       z10 <= z9 - `rot9;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x11 <= 1'b0;                        

        y11 <= 1'b0;

        z11 <= 1'b0;

    end

    else if(z10[31])

   begin

       x11 <= x10 + (y10 >>> 10);

       y11 <= y10 - (x10 >>> 10);

       z11 <= z10 + `rot10;

   end

   else

   begin

       x11 <= x10 - (y10 >>> 10);

       y11 <= y10 + (x10 >>> 10);

       z11 <= z10 - `rot10;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x12 <= 1'b0;                       

        y12 <= 1'b0;

        z12 <= 1'b0;

    end

    else if(z11[31])

   begin

       x12 <= x11 + (y11 >>> 11);

       y12 <= y11 - (x11 >>> 11);

       z12 <= z11 + `rot11;

   end

   else

   begin

       x12 <= x11 - (y11 >>> 11);

       y12 <= y11 + (x11 >>> 11);

       z12 <= z11 - `rot11;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x13 <= 1'b0;                       

        y13 <= 1'b0;

        z13 <= 1'b0;

    end

    else if(z12[31])

   begin

       x13 <= x12 + (y12 >>> 12);

       y13 <= y12 - (x12 >>> 12);

       z13 <= z12 + `rot12;

   end

   else

   begin

       x13 <= x12 - (y12 >>> 12);

       y13 <= y12 + (x12 >>> 12);

       z13 <= z12 - `rot12;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x14 <= 1'b0;                       

        y14 <= 1'b0;

        z14 <= 1'b0;

    end

    else if(z13[31])

   begin

       x14 <= x13 + (y13 >>> 13);

       y14 <= y13 - (x13 >>> 13);

       z14 <= z13 + `rot13;

   end

   else

   begin

       x14 <= x13 - (y13 >>> 13);

       y14 <= y13 + (x13 >>> 13);

       z14 <= z13 - `rot13;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x15 <= 1'b0;                       

        y15 <= 1'b0;

        z15 <= 1'b0;

    end

    else if(z14[31])

   begin

       x15 <= x14 + (y14 >>> 14);

       y15 <= y14 - (x14 >>> 14);

       z15 <= z14 + `rot14;

   end

   else

   begin

       x15 <= x14 - (y14 >>> 14);

       y15 <= y14 + (x14 >>> 14);

       z15 <= z14 - `rot14;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        x16 <= 1'b0;                       

        y16 <= 1'b0;

        z16 <= 1'b0;

    end

    else if(z15[31])

   begin

       x16 <= x15 + (y15 >>> 15);

       y16 <= y15 - (x15 >>> 15);

       z16 <= z15 + `rot15;

   end

   else

   begin

       x16 <= x15 - (y15 >>> 15);

       y16 <= y15 + (x15 >>> 15);

       z16 <= z15 - `rot15;

   end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        Quadrant[0] <= 1'b0;

        Quadrant[1] <= 1'b0;

        Quadrant[2] <= 1'b0;

        Quadrant[3] <= 1'b0;

        Quadrant[4] <= 1'b0;

        Quadrant[5] <= 1'b0;

        Quadrant[6] <= 1'b0;

        Quadrant[7] <= 1'b0;

        Quadrant[8] <= 1'b0;

        Quadrant[9] <= 1'b0;

        Quadrant[10] <= 1'b0;

        Quadrant[11] <= 1'b0;

        Quadrant[12] <= 1'b0;

        Quadrant[13] <= 1'b0;

        Quadrant[14] <= 1'b0;

        Quadrant[15] <= 1'b0;

        Quadrant[16] <= 1'b0;

    end

    else

    begin

        Quadrant[0] <= Phase[17:16];

        Quadrant[1] <= Quadrant[0];

        Quadrant[2] <= Quadrant[1];

        Quadrant[3] <= Quadrant[2];

        Quadrant[4] <= Quadrant[3];

        Quadrant[5] <= Quadrant[4];

        Quadrant[6] <= Quadrant[5];

        Quadrant[7] <= Quadrant[6];

        Quadrant[8] <= Quadrant[7];

        Quadrant[9] <= Quadrant[8];

        Quadrant[10] <= Quadrant[9];

        Quadrant[11] <= Quadrant[10];

        Quadrant[12] <= Quadrant[11];

        Quadrant[13] <= Quadrant[12];

        Quadrant[14] <= Quadrant[13];

        Quadrant[15] <= Quadrant[14];

        Quadrant[16] <= Quadrant[15];

    end

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

    begin

        Cos <= 1'b0;

        Sin <= 1'b0;

        Error <= 1'b0;

    end

    else

    begin

        Error <= z16;

        case(Quadrant[16])

            2'b00: //if the Phase is in first Quadrant,the Sin(X)=Sin(A),Cos(X)=Cos(A)

                begin

                    Cos <= x16;

                    Sin <= y16;

                end

            2'b01: //if the Phase is in second Quadrant,the Sin(X)=Sin(A+90)=CosA,Cos(X)=Cos(A+90)=-SinA

                begin

                    Cos <= ~(y16) + 1'b1;//-Sin

                    Sin <= x16;//Cos

                end

            2'b10: //if the Phase is in third Quadrant,the Sin(X)=Sin(A+180)=-SinA,Cos(X)=Cos(A+180)=-CosA

                begin

                    Cos <= ~(x16) + 1'b1;//-Cos

                    Sin <= ~(y16) + 1'b1;//-Sin

                end

            2'b11: //if the Phase is in forth Quadrant,the Sin(X)=Sin(A+270)=-CosA,Cos(X)=Cos(A+270)=SinA

                begin

                    Cos <= y16;//Sin

                    Sin <= ~(x16) + 1'b1;//-Cos

                end

        endcase

    end

end

 

endmodule

 

以下是testbench文件代码

 

`timescale 1 ps/ 1 ps

 

module Cordic_Test_tb;

 

// Inputs

reg                         CLK_50M;

reg                         RST_N;

reg             [15:0]      cnt;

reg             [15:0]      cnt_n;

reg             [31:0]      Phase;

reg             [31:0]      Phase_n;

wire            [31:0]      Sin;

wire            [31:0]      Cos;

wire            [31:0]      Error;

 

// Instantiate the Unit Under Test (UUT)

Cordic_Test                 uut

(

    .CLK_50M                (CLK_50M    ),

    .RST_N                  (RST_N      ),

    .Phase                  (Phase      ),

    .Sin                    (Sin        ),

    .Cos                    (Cos        ),

    .Error                  (Error      )

);

 

initial

begin

    #0 CLK_50M = 1'b0;

    #10000 RST_N = 1'b0;

    #10000 RST_N = 1'b1;

    #10000000 $stop;

end

 

always #10000

begin

    CLK_50M = ~CLK_50M;

end

 

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

        cnt <= 1'b0;

    else

        cnt <= cnt_n;

end

 

always @ (*)

begin

    if(cnt == 16'd359)

        cnt_n = 1'b0;

    else

        cnt_n = cnt + 1'b1;

end

 

//生成相位0-359度,Phase[17:16]为相位的象限,Phase[15:10]为相位的值

always @ (posedge CLK_50M or negedge RST_N)

begin

    if(!RST_N)

        Phase <= 1'b0;

    else

        Phase <= Phase_n;

end

 

always @ (*)

begin

    if(cnt <= 16'd90)

        Phase_n = cnt;

    else if(cnt > 16'd90 && cnt <= 16'd180)

        Phase_n = {2'd01,cnt - 16'd90};

    else if(cnt > 16'd180 && cnt <= 16'd270)

        Phase_n = {2'd10,cnt - 16'd180};

    else if(cnt > 16'd270)

        Phase_n = {2'd11,cnt - 16'd270};

end

 

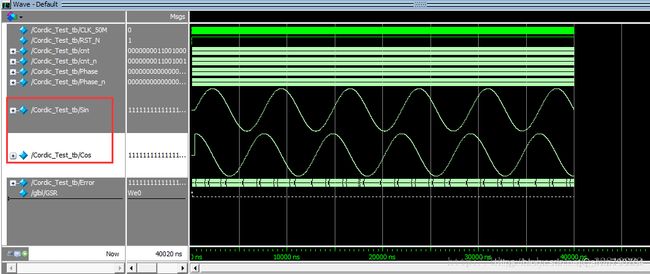
endmodule

最后来一张效果图，可以发现，我们的16级流水线已经正常的运行起来了，由于我们仿真输入的相位值为0-359度循环，因此sin和cos也循环了~~~