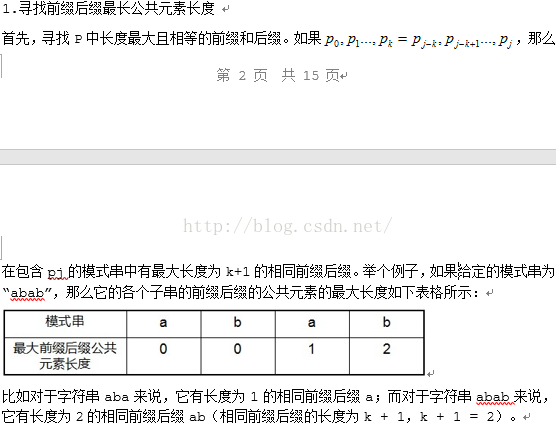
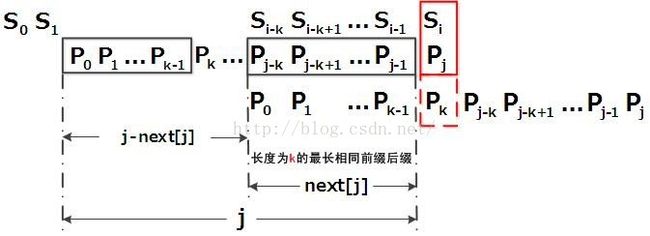
字符串匹配与AC自动机
解决字符串匹配问题,初级的算法是如下的BF算法:
从主串的第1个字符起和模式串的第一个字符比较,若相等,则继续逐个比较后续字符,否则从主串的第2字符起重新和模式串的字符比较。依次类推,直到模式串t中的每个字符依次和主串s中的一个连续的字符序列相等,则匹配成功。否则匹配不成功。如果文本串的长度为n,模式串的长度为m,BF算法最好情况下的时间复杂度是O(n+m),最坏情况下的时间复杂度是O(nm)。后来又出现了一系列时间复杂度更低的算法,如KMP算法。
一、KMP算法
所谓KMP算法,其基本思路就是:
假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置,如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符;如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。
换言之,当匹配失败时,模式串向右移动的位数=失配字符所在位置 - 失配字符对应的next 值,即移动的实际位数为j,且此值大于等于1。
next 数组各值的含义:代表当前字符之前的字符串中,有多大长度的相同前缀后缀。例如如果 next [j] = k ,代表 j 之前的字符串中有最大长度为 k 的相同前缀后缀。这也意味着在某个字符失配时,该字符对应的 next 值会告诉你下一步匹配中,模式串应该跳到哪个位置(跳到 next [j] 的位置)。如果 next [j] 等于 0 或 -1 ,则跳到模式串的开头字符,若 next [j] = k 且 k > 0 ,代表下次匹配跳到 j 之前的某个字符,而不是跳到开头,且具体跳过了 k 个字符。步骤:
综上,KMP的next 数组相当于告诉我们:当模式串中的某个字符跟文本串中的某个字符匹配失配时,模式串下一步应该跳到哪个位置。如模式串中在j 处的字符跟文本串在i 处的字符匹配失配时,下一步用next [j] 处的字符继续跟文本串i 处的字符匹配,相当于模式串向右移动 j - next[j] 位。
优化:
当p[j] != s[i] 时,下次匹配必然是p[ next [j]] 跟s[i]匹配,如果p[j] = p[ next[j] ],必然导致后一步匹配失败(因为p[j]已经跟s[i]失配,然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配,很显然,必然失配),所以不能允许p[j] = p[ next[j ]]。因此,如果出现了p[j] = p[ next[j] ],则需要再次递归,即令next[j] = next[ next[j] ]。
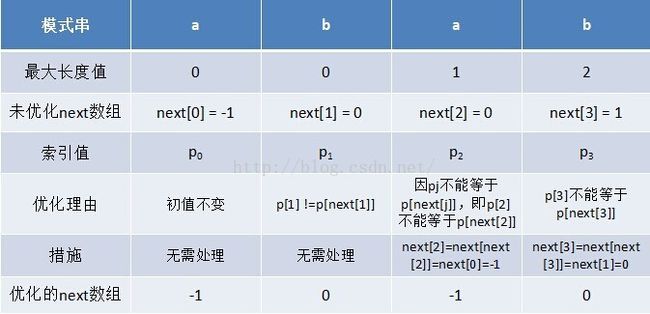
利用优化过后的next 数组求法,可知模式串“abab”的新next数组为:-1 0 -1 0。只要求出了原始next 数组,便可以根据原始next 数组快速求出优化后的next 数组。还是以abab为例,如下表格所示:
只要出现了p[next[j]] = p[j]的情况,则把next[j]的值再次递归。例如在求模式串“abab”的第2个a的next值时,如果是未优化的next值的话,第2个a对应的next值为0,相当于第2个a失配时,下一步匹配模式串会用p[0]处的a再次跟文本串匹配,必然失配。所以求第2个a的next值时,需要再次递归:next[2] = next[ next[2] ] = next[0] = -1(此后,根据优化后的新next值可知,第2个a失配时,执行“如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符”),同理,第2个b对应的next值为0。
对于优化后的next数组可以发现一点:如果模式串的后缀跟前缀相同,那么它们的next值也是相同的,例如模式串abcabc,它的前缀后缀都是abc,其优化后的next数组为:-1 0 0 -1 0 0,前缀后缀abc的next值都为-1 0 0。
KMP的时间复杂度:如果文本串的长度为n,模式串的长度为m,那么匹配过程的时间复杂度为O(n),算上计算next的O(m)时间,KMP的整体时间复杂度为O(m + n)。
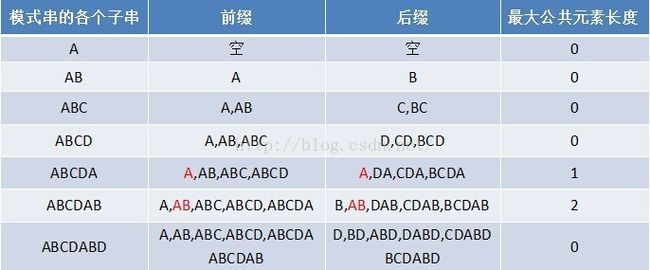
如果给定的模式串是:“ABCDABD”,从左至右遍历整个模式串,其各个子串的前缀后缀分别如下表格所示:
给定文本串“BBCABCDABABCDABCDABDE”,和模式串“ABCDABD”,现在要拿模式串去跟文本串匹配,因为模式串中的字符A跟文本串中的字符B、B、C、空格一开始就不匹配,所以不必考虑结论,直接将模式串不断的右移一位即可,直到模式串中的字符A跟文本串的第4个字符A匹配成功。继续往后匹配,当模式串最后一个字符D跟文本串匹配时失配,显而易见,模式串需要向右移动。但向右移动多少位呢?因为此时已经匹配的字符数为6个(ABCDAB),然后根据最大长度表可得失配字符D的上一位字符B对应的长度值为2,所以根据之前的结论,可知需要向右移动6 - 2 = 4 位。
模式串向右移动4位后,发现C处再度失配,因为此时已经匹配了2个字符(AB),且上一位字符B对应的最大长度值为0,所以向右移动:2 - 0 =2 位。
继续比较,发现D与C 失配,故向右移动的位数为:已匹配的字符数6减去上一位字符B对应的最大长度2,即向右移动6 - 2 = 4 位。
经历第5步后,发现匹配成功,过程结束。
问题的关键就是寻找模式串中最大长度的相同前缀和后缀,找到了模式串中每个字符之前的前缀和后缀公共部分的最大长度后,便可基于此匹配。而这个最大长度便正是next 数组要表达的含义。
失配时,模式串向右移动的位数 = 已匹配字符数 - 失配字符的上一位字符所对应的最大长度值。上文利用这个表和结论进行匹配时,我们发现,当匹配到一个字符失配时,其实没必要考虑当前失配的字符,更何况我们每次失配时,都是看的失配字符的上一位字符对应的最大长度值。如此,便引出了 next 数组。求取next数组的算法:void getNext(string s, int *next){
int n = s.length(), i = 0, j = -1;
next[0] = -1;
while (i < n - 1)
{
if (j == -1 || s[i] == s[j])
next[++i] = ++j;
else
j = next[j];
}
}把next 数组跟之前求得的最大长度表对比后,不难发现,next 数组相当于“最大长度值” 整体向右移动一位,然后初始值赋为-1。因此,next 数组的求解就是找最大对称长度的前缀后缀,然后整体右移一位,初值赋为-1,也可以直接计算某个字符对应的next值,就是看这个字符之前的字符串中有多大长度的相同前缀后缀。
无论是基于最大长度表的匹配,还是基于next 数组的匹配,两者得出来的向右移动的位数是一样的。根据最大长度表,失配时,模式串向右移动的位数 = 已经匹配的字符数 - 失配字符的上一位字符的最大长度值,而根据next 数组,失配时,模式串向右移动的位数 = 失配字符的位置 - 失配字符对应的next 值。其中,从0开始计数时,失配字符的位置 = 已经匹配的字符数(失配字符不计数),而失配字符对应的next 值 = 失配字符的上一位字符的最大长度值,两相比较,结果必然完全一致。所以,可以把最大长度表看做是next 数组的雏形,甚至就把它当做next 数组也是可以的,区别不过是怎么用的问题。
基于next 数组进行匹配和上述过程等价,但是这样做在计算上更为麻烦,而最大前缀后缀的公共元素的长度值是显然的,next 数组确实是只要将各个最大前缀后缀的公共元素的长度值右移一位,且把初值赋为-1 即可。代码如下:
int kmp(string s, string t){
/*这里输出的是S开始和T匹配的位数*/
int n1 = s.length(), n2 = t.length(), i = 0, j = 0;
int *next = new int[n2];
getNext(t, next);
while (iEXTERN-KMP算法要求出字符串B的后缀与字符串A的最长公共前缀,extend[i]表示B[i...B_len] 与A的最长公共前缀长度,也就是要计算这个数组,利用它直接解决匹配问题,只要看extend[]数组元素是否有一个等于len_A即可。显然这个数组保存了更多更丰富的信息,即B的每个位置与A的匹配长度。计算这个数组extend也采用了于kmp类似的过程。首先也是需要计算字符串A与自身后缀的最长公共前缀长度。我们设为next[]数组。当然这里next数组的含义与kmp里的有所过程。但它的计算,也是利用了已经计算出来的next[1...i-1]来找到next[i]的大小,整体的思路是一样的。
首先在1...i-1,要找到一个k,使得它满足k+next[k]-1最大,也就是说,让k加上next[k]长度尽量长。然后设len= k+next[k]-1:
1°len < i 也就是说,len的长度还未覆盖到next[i],这样我们只要从头开始比较next[i...n]与next的最长公共前缀即可,这种情况下很明显的,每比较一次,必然就会让i+next[i]-1增加1;
2°len ≥ i且L = next[i-k+1] >= len-i+1,则next[i]≥len-i+1,然后我们再从此处开始比较后面的还能否匹配,显然如果多比较一次,也会让i+A[i]-1多增加1;
3°len ≥ i且 L < len-i+1 ,next[i]的值就是L。
这样next[i]的值就被计算出来了。
二、TRIE树、AC自动机与TRIE图
Trie树又名字典树,从字面意思即可理解,这种树的结构像英文字典一样,相邻的单词一般前缀相同,之所以时间复杂度低,是因为其采用了以空间换取时间的策略。其节点:
class Node{
public:
int count; //记录该处字符串个数
Node* char_arr[NUM]; //分支
char* current_str; //记录到达此处的路径上的所有字母组成的字符串
Node();
};将每个字符串插入到trie树中,到达特定的结尾节点时,在这个节点上进行标记,如插入"afb",第一个字母为a,沿着a往下,然后第二个字母为f,沿着f往下,第三个为b,沿着b往下,由于字符串最后一个字符为'\0',因而结束,不再往下了,然后在这个节点上标记afb.count++,即其个数增加1之后,通过前序遍历此树,即可得到字符串从小到大的顺序。
class Trie{
public:
Node* root;
Trie();//构造函数略
void insert(char* str){
int i = 0;
Node* parent = root;
while(str[i] != '\0'){
if(parent->char_arr[str[i] - 'a'] == NULL){
parent->char_arr[str[i] - 'a'] = new Node();
strcat(parent->char_arr[str[i] - 'a']->current_str, parent->current_str);
char str_tmp[2];
str_tmp[0] = str[i];
str_tmp[1] = '\0';
strcat(parent->char_arr[str[i] - 'a']->current_str, str_tmp);
parent = parent->char_arr[str[i] - 'a'];
}
else{
parent = parent->char_arr[str[i] - 'a'];
}
i++;
}
parent->count++;
}
void output(Node* &node, char** str, int& count){
if(node != NULL){
if(node->count != 0){
for(int i = 0; i < node->count; i++){
str[count++] = node->current_str;
}
for(int i = 0; i < NUM; i++){
output(node->char_arr[i], str, count);
}
}
}
}
};AC自动机,可以看成是kmp在多字符串情况下扩展形式,可以用来处理多模式串匹配。只要为这些模式串建立一个trie树,然后再为每个节点建立一个失败指针,也就是类似与kmp的next函数,让我们知道如果匹配失败,可以再从哪个位置重新开始匹配。
在kmp构造next数组时,我们是从前往后构造,即先构造1...i-1,然后再利用它们计算next[i],这里也是类似。不过这个先后,是通过bfs的顺序来体现的。AC自动机的失败指针具有同样的功能,也就是说当我们的模式串在Tire上进行匹配时,如果与当前节点的关键字不能继续匹配的时候,就应该去当前节点的失败指针所指向的节点继续进行匹配。而从根到这个失败指针指向的节点组成的字符串,实际上就是跟当前节点的后缀的匹配最长的字符串。
如同KMP中模式串得自我匹配一样.从根节点开始,对于每个结点:设该结点上得字符为k,沿着其父亲结点得失败指针走,直到到达根节点或者当前失败指针结点也存在字符为k的孩子结点,那么前一种情况当然是把失败指针设为根节点,而后一种情况则设为当前失败指针结点得字符为k的孩子结点。接下来要做的就是进行文本匹配:首先,Trie-(模式串集合)中有一个指针p1指向root,而文本串中有一个指针p2指向串头。下面的操作和KMP很类似:如果设k为p2指向的字母 ,而在Trie中p1指向的节点存在字符为k的儿子,那么p2++,p1则改为指向那个字符为k的儿子,否则p1顺着当前节点的失败指针向上找,直到p1存在一个字符为k的儿子,或者p1指向根结点。如果p1路过一个标记为模式串终点的结点,那么以这个点为终点的的模式串就已经匹配过了.或者如果p1所在的点可以顺着失败指针走到一个模式串的终结结点,那么以那个结点结尾的模式串也已经匹配过了。
trie图实际上一个确定性自动机,比ac增加了确定性这个属性,对于ac自动机来说,当碰到一个不匹配的节点后可能要进行好几次回溯才能进行下一次匹配。但是对于trie图来说,可以每一步进行一次匹配,每碰到一个输入字符都有一个确定的状态节点。
从上面的图中我们也可以看到trie图的后缀节点跟ac自动机的后缀指针基本一致,区别在于trie图的根添加了了所有字符集的边。另外trie图还会为每个节点补上所有字符集中的字符的边,而这个补边的过程实际上也是一个求节点的后缀节点的过程,不过这些节点都是虚的,我们不把它们加到图中,而是找到它们的等价节点即它们的后缀节点,从而让这些边指向后缀节点就可以了。(比如上图中的黑节点c,它实际上并未出现在我们的初始tire里,但我们可以把它作为一个虚节点处理,把指向它的边指向它的后缀节点)
trie图主要利用两个概念实现这种目的。一个是后缀节点,也就是每个节点的路径字符串去掉第一个字符后的字符串对应的节点。计算这个节点的方法,是通过它父亲节点的后缀节点,很明显它父亲的后缀节点与它的后缀节点的区别就是还少一个尾字符,设为c。所以节点的父节点的指针的c孩子就是该节点的后缀节点。但是因为有时候它父亲不一定有c孩子,所以还得找一个与父亲的c孩子等价的节点。于是就碰到一个寻找等价节点的问题。
而trie图还有一个补边的操作,不存在的那个字符对应的边指向的节点实际上可以看成一个虚节点,我们要找一个现有的并且与它等价的节点,将这个边指向它。这样也实际上是要寻找等价节点。
我们看怎么找到一个节点的等价节点,我们所谓的等价是指它们的危险性一致。那我们再看一个节点是危险节点的充要条件是:它的路径字符串本身就是一个危险单词,或者它的路径字符串的后缀对应的节点是一个危险节点。因此我们可以看到,如果这个节点对应的路径字符串本身不是一个危险单词,那它就与它的后缀节点是等价的。所以我们补边的时候,实际指向的是节点的后缀节点就可以了。
trie图实际上对trie树进行了改进,添加了额外的信息。使得可以利用它方便的解决多模式串的匹配问题。跟kmp的思想一样,trie图也是希望利用现在已经匹配的信息,对未来的匹配提出指导。提出了一些新的概念。定义trie树上,从根到某个节点的路径上所有边上的字符连起来形成的字符串称为这个节点的路径字符串。如果某个节点的路径字符串以一个危险字符串结尾,那么这个节点就是危险节点:也就是说如果到达这个点代表是匹配的状态;否则就是安全节点。那么如何判断某个节点是否危险呢?
根节点显然是安全节点。一个节点是危险节点的充要条件是:它的路径字符串本身就是一个危险单词,或者它的路径字符串的后缀(这里特指一个字符串去掉第一个字符后剩余的部分)对应的节点(一个字符串对应的节点,是指从trie图中的根节点开始,依次沿某个字符指定的边到达的节点)是一个危险节点。
那么如何求每一个节点的后缀节点呢?这里就可以利用以前的计算信息得到了。具体来说就是利用父亲节点的后缀节点,我们只要记住当前节点的最后一个字符设为C,那么父亲节点的后缀节点的C分支节点就是要求的后缀节点了。首先我们限定,根节点的后缀节点是根本身,第一层节点的后缀节点是根节点。这样我们可以逐层求出所有节点的后缀节点。设当前节点的父亲节点的后缀节点为w,我们假设w具有c子树,我们可以看到对于w的整个c子树来说,因为根本不存在通向它们的边c,它们也就不可能是不良字符串,这样这些节点的危险性也就等价与它们的后缀节点的危险性了,而它们的后缀节点,实际上就是w的后缀节点的c孩子,如此回溯下去,最后就能找到。
三、DFA与NFA
一个确定的有限自动机(DFA)M可以定义为一个五元组,M=(K,∑,F,S,Z),其中:
(1) K是一个有穷非空集,集合中的每个元素称为一个状态;
(2) ∑是一个有穷字母表,∑中的每个元素称为一个输入符号;
(3) F是一个从K×∑→K的单值转换函数,即F(R,a)=Q,(R,Q∈K)表示当前状态为R,如果输入字符a,则转到状态Q,状态Q称为状态R的后继状态;
(4) S∈K,是惟一的初态;
(5) ZK,是一个终态集。
由定义可见,确定有限自动机只有惟一的一个初态,但可以有多个终态,每个状态对字母表中的任一输入符号,最多只有一个后继状态。
对于DFA M,若存在一条从某个初态结点到某一个终态结点的通路,则称这条通路上的所有弧的标记符连接形成的字符串可为DFA M所接受。若M的初态结点同时又是终态结点,则称ε可为M所接受(或识别),DFA M所能接受的全部字符串(字)组成的集合记作L(M)。
一个不确定有限自动机(NFA)M可以定义为一个五元组,M=(K,∑,F,S,Z),其中:
(1) k是一个有穷非空集,集合中的每个元素称为一个状态;
(2) ∑是一个有穷字母表,∑中的每个元素称为一个输入符号;
(3) F是一个从K×∑→K的子集的转换函数;
(4) SK,是一个非空的初态集;
(5) ZK,是一个终态集。
由定义可见,不确定有限自动机NFA与确定有限自动机DFA的主要区别是:
(1)NFA的初始状态S为一个状态集,即允许有多个初始状态;
(2)NFA中允许状态在某输出边上有相同的符号,即对同一个输入符号可以有多个后继状态。即DFA中的F是单值函数,而NFA中的F是多值函数。
因此,可以将确定有限自动机DFA看作是不确定有限自动机NFA的特例。和DFA一样,NFA也可以用矩阵和状态转换图来表示。
对于NFA M,若存在一条从某个初态结点到某一个终态结点的通路,则称这条通路上的所有弧的标记(ε除外)连接形成的字符串可为M所接受。NFA M所能接受的全部字符串(字)组成的集合记作L(M)。
由于DFA是NFA的特例,所以能被DFA所接受的符号串必能被NFA所接受。
设M和N是同一个字母集∑上的有限自动机,若L(M)=L(N),则称有限自动机M和N等价。
由以上定义可知,若两个自动机能够接受相同的语言,则称这两个自动机等价。DFA是NFA的特例,因此对任意NFA M总存在一个DFA N,使得L(M)=L(N)。即一个不确定有限自动机能接受的语言总可以找到一个等价的确定有限自动机来接受该语言。
同一个字符串α可以由多条通路产生,而在实际应用中,作为描述控制过程的自动机,通常都是确定有限自动机DFA,因此这就需要将不确定有限自动机转换成等价的确定有限自动机,这个过程称为不确定有限自动机的确定化,即NFA确定化为DFA。
下面介绍一种NFA的确定化算法,这种算法称为子集法:
若NFA的全部初态集合为S,则令DFA的初态为S;
(1) 设DFA的状态集K中有一状态为S(i_to_j)(Si到Sj所有元素的集合,是S的子集),若对某符号a∈∑,在NFA中有F{[S(i_to_j) ],a}=S′(i_to_k),则令F为DFA的一个转换函数。若S′(i_to_k)不在K中,则将其作为新的状态加入到K中。
(2) 重复第2步,直到K中不再有新的状态加入为止。
(3) 上面得到的所有状态构成DFA的状态集K,转换函数构成DFA的F,DFA的字母表仍然是NFA的字母表∑。
(4) DFA中凡是含有NFA终态的状态都是DFA的终态。
对于上述NFA确定化算法——子集法,还可以采用另一种操作性更强的描述方式,下面我们给出其详细描述。首先给出两个相关定义。
假设I是NFAM状态集K的一个子集(即I∈K),则定义ε-closure(I)为:
(1) 若Q∈I,则Q∈ε-closure(I);
(2) 若Q∈I,则从Q出发经过任意条ε弧而能到达的任何状态Q’,则Q’∈ε-closure(I)。
状态集ε-closure(I)称为状态I的ε闭包。
假设NFA M=(K,∑,F,S,Z),若I∈K,a∈∑,则定义Ia=ε-closure(J),其中J是所有从ε-closure(I)出发,经过一条a弧而到达的状态集。
NFA确定化的实质是以原有状态集上的子集作为DFA上的一个状态,将原状态间的转换为该子集间的转换,从而把不确定有限自动机确定化。经过确定化后,状态数可能增加,而且可能出现一些等价状态,这时就需要简化。代码如下:
#include
#include
#define MAXS 100
using namespace std;
string NODE;
string CHANGE;
int N; //NFA edges
struct edge{
string first;
string change;
string last;
};
struct chan{
string ltab;
string set[MAXS];
};
void IsEmpty(int a){
int i;
for(i=0;iNODE.find(a[i+1])){
b=a[i];
a[i]=a[i+1];
a[i+1]=b;
}
}
}
}
void eclosure(char c,string &he,edge b[]){
int k;
for(k=0;khe.length()){
he+=b[k].last;
eclosure(b[k].last[0],he,b);
}
}
}
}
}
void move(char &he,int m,edge b[]){
int i,j,k,l;
k=he.ltab.length();
l=he.set[m].length();
for(i=0;ihe.set[m].length()){
he.set[m]+=b[j].last[0];
}
}
}
}
for(i=0;ihe.set[m].length()){
he.set[m]+=b[j].last[0];
}
}
}
}
}
/*output*/
void outputfa(int len,int h,chan *t){
int i,j,m;
cout<<" I ";
for(i=0;i>b[i].first;
if(b[i].first=="#"){
break;
}
cin>>b[i].change>>b[i].last;
}
N=i;
for(j=0;jNODE.length()){
NODE+=b[i].first;
}
if(NODE.find(b[i].last)>NODE.length()){
NODE+=b[i].last;
}
if((CHANGE.find(b[i].change)>CHANGE.length())&&(b[i].change!="*")){
CHANGE+=b[i].change;
}
len=CHANGE.length();
}
cout<<"endnode:"<>endnode;
for(i=0;iNODE.length()){
cout<<"error"<";
move(t[i],k,b);
cout其实Trie图所起到的作用就是建立一个确定性有限自动机DFA,图中的每点都是一个状态,状态之间的转换用有向边来表示。Trie图是在Tire的基础上补边过来的,其实他应该算是AC自动机的衍生,AC自动机只保存其后缀节点,在使用时再利用后缀节点进行跳转,并一直迭代到找到相应的状态转移为止,这个就是KMP的思想。
而Trie图直接将AC自动机在状态转移计算后的值保存在当前节点,使得不必再对后缀节点进行迭代。所以Trie图的每个节点都会有|∑|个状态转移(∑指字符集)。流程:
(1)构建Trie,并保证根节点一定有|∑|个儿子。
(2)层次遍历Trie,计算后缀节点,节点标记,没有|∑|个儿子的对其进行补边。
后缀节点的计算:
(1)根结点的后缀节点是它本身。
(2)处于Trie树第二层的节点的后缀结点也是根结点。
(3)其余节点的后缀节点,是其父节点的后缀节点中有相应状态转移的节点(这里类似AC自动机的迭代过程)。
节点标记:
(1)本身就有标记。
(2)其后缀节点有标记。
补边:用其后缀节点相应的状态转移来填补当前节点的空白。
最后Trie图中任意一个节点均有相应的状态转移,我们就用这个状态转移做动态规划。
设dp[i][j]表示第i个状态产生j个字符时,与DNA序列最小的改变值。
假设Tire图中根节点是0,则初始化dp[0][0]=1。
其后,对图进行BFS遍历,可知处于第j层时,就说明以产生了j长度的字符串。
http://www.cnblogs.com/shuaiwhu/archive/2012/05/05/2484676.html
http://duanple.blog.163.com/blog/static/709717672009825004092/
http://blog.csdn.net/hpugym/article/details/52276181?locationNum=3&fps=1
http://www.cs.uku.fi/~kilpelai/BSA05/lectures/slides04.pdf