利用体素的自相似性进行立体建模（完整版翻译）

利用体素的自相似性进行立体建模（完整版翻译）

Eric Parker

Tushar Udeshi

 

Exploiting Self-Similarity in Geometry for Voxel Based Solid Modeling, Parker, E. , Udeshi, T. , Journal of Computing & InformationScience in Engineering, 2003

 

摘要

分布式建模技术以其鲁棒性和灵活性著称。然而,其有三个主要的缺点:(1)内存需要密集,因为需要大量的像素点代表高分辨率模型；(2)计算代价高昂,因为需要访问大量的体素；(3)将等值面提取可视化代价高昂。我们描述的技术利用自相似性的数据消弭这些弊端，使得体素技术实用和有吸引力。我们将描述我们的算法、MEMS仿真过程、等值面提取和可视化过程。

分类和主题描述符

I.3.5[计算几何和对象建模]:曲线,表面,立体建模

J.6(计算机辅助工程):计算机辅助设计

一般类别

算法、性能、可靠性。

关键字

分布数据结构和算法、MEMS过程、仿真、等值面提取、可视化。

 

1 介绍

三维图形的建模、加工和可视化其像素点都受到关注。体素的原始体元由普通分区的、类比2D的3D空间组成，三维图形通常从实践——如计算机辅助体层扫描术（CAT）、磁共振成像(MRI)、流体动力学、共焦显微镜和科学实验的数据可视化过程——中来，源于对数据的采集和仿真，体素代表一个立方体的空间区样本数据集。数据存储在不同的体素中。简单的，例如利用CAT扫描密度标量；复杂的，如用于天气预报的标量或矢量场数据——压力、速度、温度和风向。

三维图形也被应用于更纯粹的几何图形问题,如CAD模型[6],拓扑简化[19],雕刻[3]，其生机勃勃的原因在于:对体素的操作本质上是简单而且鲁棒性强的，即使对于复杂模型亦如鱼得水，它提供了一个和实然相统一的模型。其相关算法也更容易开发和验证：没有需要创建多对互作的特殊情形；模型的正确性是可验证的，因为模型是可枚举的；此外,数值的稳定性增强,因为几何特征是被隐式呈现的。

基于边界呈现（B-rep）的或基于立体建构（CSG）的几何存储可以转换为体素形式，称为扫描转换[17]。这一转换对位置信息是无损的[14]，几何和体积数据翻似泾渭合流。例如,油田在建模过程中可能同时使用了三维的地形数据和油井的几何坐标。体积网格技术[18]将被应用来生成一个单一的有限元网格，以资模拟油层中的流体流动。

还应该意识到体素的一个负面影响——离散特性[4]，旋转和缩放这样的转换会导致失真，甚至不得不重新采样，如果转换反复进行，情况就将雪上加霜。同时,法平面和其他明确的几何特性的立体模型需要在隐式表达后再进行扫描转换，尽快可以运用滤波恢复，然而这一过程可能导致失真。但是最糟糕的问题是，这一算法是立方阶的，又得存储和计算大量的体素和数组，若数据是随机的或高熵的，计算代价就会很高昂，并且没有什么办法可以降低存储需求。幸而典型的人造物体体积分布并非随机，这意味着，若使用标准的图像压缩技术，存储需求可能会减少,但计算成本仍然很高。

在本文中,我们介绍了共享八叉树数据结构和缓存系统来纾解这些问题。基于八叉树[13]的共享八叉树数据可以利用自相似性的数据结构来实现惊人的压缩率与规则的几何数据集。因为我们是站在前人的肩上，我们便要首先声明我们工作中那些前无古人的部分，那就是我们在第2节引入共享八叉树数据结构的描述，即使对于一般数据，这一做法也将达到惊人的压缩比。而在第3节,我们将提出一个新颖的方案，来加速任何合适的基于八叉树算法的数据压缩到共享八叉树的进程。第5.2和5.3节描述我们如何直接从共享八叉树提取等值面作为分层splat树，而splat的层次结构使等值面适合实时的可视化，这也是我们首创的。虽然第6节中的连接组件寻找算法并非簇新，我们仍然利用扩展其匹配的方式，描述与此相关的警告。

此外,第4节描述了如何应用共享八叉树数据结构，在Zyvex开发的MEMulator™上进行MEMS仿真，尽管所有的例子都是基于MEMS的，操作却是纯粹的几何问题。

 

2 数据呈现

在描述数据结构之前,我们将首先回顾一些定义。容积细分方法将3D数据压缩在一个类似2D像素数组的常规数组中, 所有体素都有相同的大小和形状(即一个立方体)。八叉树数据结构提供了一个层次结构不失一般性的组织体素的方法，它要求空间细分为一个个立方体,在立方体的边缘，体素分辨率是2的幂。这可能需要邻域有足够的空体素建构八叉树。在实践中,这一做法是廉价的，因为特殊的“空”指标可以用来表明八叉树的中间节点均匀充满了相同的体素数据。这样一个有着特殊的指针值的八叉树被称为“自适应”八叉树。可以非常高效地、显式地呈现一个表面或流形[10]。单个像素点仍是必需的，但特殊的节点从两侧空白区域的表面起随着距离递增，这一算法是平方阶的，而完整的八叉树存储算法是立方阶的。

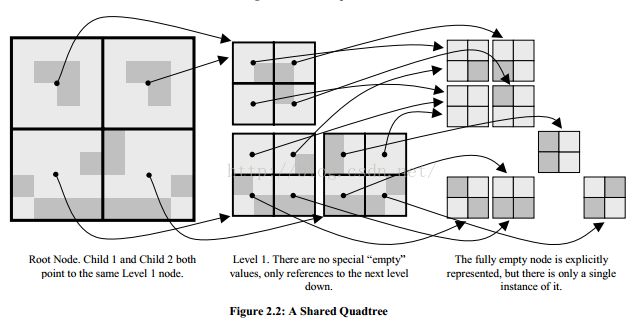
在[11]中,Bill Gosper为康威游戏（康威游戏是由3条规则构成的二维元胞自动机，由英国数学家康威于1970年提出。游戏在一个类似于围棋棋盘一样的，可以无限延伸的二维方格网中进行。例如，设想每个方格中都可放置一个生命细胞，生命细胞只有两种状态：“生”或“死”。图中，用黑色的方格表示该细胞为“生”, 空格表示该细胞为“死” 。游戏开始时, 每个细胞可以随机地或给定地被设定为“生”或“死”之一的某个状态, 然后，再根据规则计算下一代每个细胞的状态：(a)每个细胞的状态由该细胞及周围八个细胞上一次的状态所决定；(b)如果一个细胞周围有3个细胞为生，则该细胞为生，即该细胞若原先为死，则转为生，若原先为生，则保持不变；(c)如果一个细胞周围有2个细胞为生，则该细胞的生死状态保持不变，在其它情况下，该细胞为死，即该细胞若原先为生，则转为死，若原先为死，则保持不变。——译者注）描述了一种算法，每一个由各异的2^n个细胞代表的生命改由共享四叉树的单个节点表征。每一个这样的节点空间分为四个2^(n– 1)孩子节点,进而也被独一无二地代表。无论是否包含“生命”，递归都可以终止于1×1节点，实际上是一个二进制值。无论模拟“宇宙”有多大，都只需要两个1×1节点。这一共享四叉树结构可以推广到三维空间的八叉树，并且非二进制数据也可以通过创建一个节点为每个独特的体素值——包括标量、向量,或任何其他类型的数据——进行存储。

八叉树的每个大小为2的幂的节点空置，其指针值在自适应八叉树中可被视为等同于特殊空值，除非有logn的部分在共享八叉树中，因此,自适应八叉树是共享八叉树的一个子集。然而,共享八叉树也利用自相似性数据,这给压缩提供了更多的机会。我们将说明在二维情形使用四叉树的相关概念。

如图2.1所示，一种自适应四叉树数据结果存储于一个零级节点（根节点） (8×8),四个一级节点(4×4),十二个二级节点(2×2)，只有十二个——而非十六个——二级节点是必需的，因为有四个节点统一空置。

现在我们将考虑共享四叉树如图2.2所示。我们从一个零级节点开始,但是现在只有三个一级节点，因为在总共四个节点中有两个是相同的。虽然我们现在必须显式存储完全空节点，但叶节点的数量缩减到8，为每个级别创建全空节点是必要的，这最多需要logn的额外节点，而自适应四叉树并不显式存储空节点。

一个共享的八叉树可以由体素通过访问体素数组，递归地、自底向上地构建八叉树：

OctNode* BuildSharedOctree(Voxel voxels[n][n][n], int n, int size, int x, int y, int z) 
{ 
if (size == 1)  { 
    return (OctNode*);
    FindVoxel(voxels[x][y][z]); 
} 
OctNode* node = new OctNode;   
int sz = size/2;  
node->child[0] = BuildSharedOctree(voxels, n, sz, x,y,z); 
node->child[1] = BuildSharedOctree(voxels, n, sz, x+sz, y ,z); 
//… 
node->child[7] = BuildSharedOctree(voxels, n, sz, x+sz, y+sz, z+sz); 
return FindNode(node); 
}

其中n是压缩的一维数组的长度，size是在建子树的大小，函数首次调用时size=n，x,y,z是左侧、下侧、前端子树的球坐标，FindNode(OctNode *node)返回OctNode的唯一实例，如同孩子节点一样。散列表或基于八个孩子指针的字典可资运用，如果节点在字典里未及觅得，那么它应该插入到字典中，返回FindNode ()之结果。FindVoxel(Voxel *voxel)与FindNode()相似，但返回体素的实例，参数不变。

压缩的实现显然是非常依赖数据的，然而,一些一般性的观察表明极坐标数据更能精确匹配。数组的重复结构也将很好地工作。我们正在扩展功能，以便共享不仅共享确切的匹配，而且更好的拟合多样的数据，例如CAT扫描和地形图。在实践中,我们发现许多看似臃肿和复杂的结构在精确匹配（超过99.9%）的前提下可以被大大压缩。

数组大小49754718720字节

自适应八叉树大小11900655552字节

共享八叉树大小24640088字节

满八叉树储存99.95%

 

3 结果匹配

与自适应八叉树相比，共享八叉树是向后兼容的完整的八叉树的算法，换句话说,一个递归程序访问八个孩子节点不需要意识到这是在多次访问相同的孩子节点。考虑一个简单的程序,计算非空的像素点的总数:

int Count(OctNode* node, int size)
{ 
if (size == 1)    return ((Voxel*)node)->value != 0;  
// return 1 if non-empty   
int sum = 0;   
for (int i = 0; i < 8; i++) { 
    sum += Count(node->child[i], size/2); 
}
return sum; 
}

子树非空体素的数量独立于其球坐标——关键是体素的内容。我们可以为每个节点缓存加和以资计算，如果相同的节点指针值再次被觅得，我们可以简单地返回保存的加和，而不必访问任何孩子节点，因为在共享八叉树的每个子树中只有一个实例共享。我们已经将一个立方阶算法简化为线性的。实际上，通过共享八叉树数据结构，结果匹配提高了任何合适的八叉树算法的性能——压缩比。

这一算法必须满足两个标准:

1.缓存的键必须从本地或计算“相对”数据的子树节点；

2.操作必须是确定的。

每一个节点的球坐标都是独特的，并且可以通过八叉树的邻域量度，其数据与给定子树的节点相关联，其操作还不仅限于计算标量，而可能是八叉树本身的革新。然而,不能简单地改变节点或体素的内容，因为节点前后相关。相反,一个新的树必须递归构造,最后一步是将根指针由指向老树改为指向新树。考虑以下在x方向上将所有体素+ 1的算法：

/* 
index is the child index of node with respect to its parent node. 
parents is a push-down stack of parent nodes and their child indices. 
*/ 
OctNode* Translate1X(OctNode* node, int size, int index, OctNodeStack parents) 
{ 
/* 
GetNeighbor() finds a neighboring node at some delta by following the stack of parent nodes. 
This function will work at any level of the tree. See [13] for more details. 
*/ 
 if (size == 1)  return GetNeighbor(parents, index, -1, 0, 0); 
 OctNode* dest = new OctNode;  
 parents.push(node, index); 
 for (int i = 0; i < 8; i++){  
     dest->child[i] = Translate1X(node-> child[i], size/2, i, parents); 
     parents.pop(); 
 }
return FindNode(dest); 
/* 
The FindNode() guarantees uniqueness. The shared octree is used for compression only 
*/  
} 

现在加上结果匹配。

OctNode* Translate1X(OctNode* node, int size, int index, OctNodeStack parents) 
{ 
OctNode* neighbor = GetNeighbor(parents, index, -1,0,0); 
 if (size == 1)  return neighbor; 
 // check for a matching result  OctNode* dest = FindResult(node, neighbor); 
 if (dest != NULL)  return dest; 
 // No match, so create a new result   dest = new OctNode;  parents.push(node, index); 
 for (int i = 0; i < 8; i++) { 
     dest->child[i] = Translate1X(node-> child[i], size/2, i, parents); 
     parents.pop(); 
     dest = FindNode(dest); 
 }
// Guarantee uniqueness 
/* Add dest as the result for the key composed of node and neighbor */ 
 AddResult(node, neighbor, dest);  
return dest; 
}

用于匹配结果的关键是给定的组合节点和x轴左侧的邻居节点。这是真正在树的水平执行的，因为需要考察那些相对左侧的节点以资平移，该算法可以很容易地修改，以期平移任意距离，要求GetNeighbor()返回的节点集包含潜在源体素(最多两次同轴平移),结果是这些源节点加上给定节点的和。

新树遽生，老树犹存。这一事实可以用来有效地保存所有处理的完整历史，只要保存一个存储每棵树的根指针的链表，而新树郁郁青青。这种方法优于仅仅那些树间的三角阵地进行计算的战斗，因为只有革新的数据增加了存储成本，而每棵树仍然被视为完整的八叉树。

可以通过最小化关键集的大小提高性能。对于一棵自适应的八叉树，应该留心找到最小的也是最关键的设置，显然，结果匹配只有当重逢时才熠熠生辉，因此，匹配结果取决于将数据压缩在共享八叉树数据结构的效率。

4 MEMS工艺模拟

微机电系统(MEMS)是通过各种微加工技术制造的，主要用于微米尺寸机电加工，在表面微加工、重复光刻技术、沉积和蚀刻生产机械设备表面的硅片、制造专门机器如“低压化学沉积炉”“离子反应腐蚀装置”“临界干燥装置”和“金属溅射装置”。整个表面微加工过程模拟起来是很复杂的。但是，如果我们假设工程师技艺纯熟，那么最终的努力可能会以简单的几何操作呈现。

例如,低压化学汽相淀积(LPCVD)将气体保形沉积到每一个给定材料的暴露硅片表面。沉积材料的构建期间，处理步骤速率恒定。一个将结果可视化的方法是，设想一个在表面滑动的小球，其结果是球的每一个位置的集合的体积包络，相当于图像处理中的扩张。另一个常见的操作——反应离子刻蚀(RIE)中，平行光束轰击晶体上的活化离子，离子在暴露的硅或其他材料上反应，腐蚀了一小部分材料。然而,离子并不与材料反应，因为材料表面有遏止蚀刻的膜。反应的几何结果是一个向下平移的拓扑面，直到蚀刻达到最大距离——反应停止，或接触到遏止蚀刻的膜。

传统的模拟MEMS中的[2,9,20]使用立体几何内核执行各种操作，这一技术鲁棒性并不强,不能产生精确的几何图形。例如，LPCVD是一个各向同性的沉积，然而,模拟LPCVD立体建模的抵消操作不灵敏，在尖角产生了大量的错误，边缘的几何误差将达到27.3%。而且这一操作可能导致复杂的表面，如图4.1所示。这些自我检测和循环的数值不稳定，抵消操作常常失败[20]。

图4.1：左为传统方法生成的图形，右为MEMS生成的图形。

对于MEMS，之前也曾使用过分布式方法进行过程模拟[16],但域的大小是有限的，且需要大量的计算资源。共享八叉树及结果匹配在MEMulator™上实现了对产品加工的仿真。无论是保形沉积和蚀刻，还是直接腐蚀和沉积都易于实现。这两个操作将数据存储到一个共享四叉树，其与共享八叉树异曲同工，两个数据结构可以同时运作。八叉树终止在大小为4之处，由是有64个体素数组存储于八叉树的叶节点，这有助于减少从每个八叉树节点的8个指针存储的开销。

我们将体积流形技术[10]推广，来存储多块材料上的数据组成的八叉树。各体素数据可能源自两块不同的材料。我们将标量进行压缩，以资追踪第一块材料上的数据的体积占比，然后压缩第二块材料的数据的一部分，这一压缩是离散化的，也是可以由一块材料的情形推广的。表面的位置可以根据曲面法向量的方向隐式地定义，总表面是各面元近似的线性组合。我们从每个位于表面的体素出发，填充整个空间，其邻域的沉积过程以向量表示，向量的方向从源体素指向每个潜在目标体素。

下面计算目标体素的裂缝，如果新的计算值大于当前值，那么就更新当前值。该算法复杂度为O(n^2·m^3)(m是球的半径)。若无结果匹配算法，则这样的飞跃是不可想象的。我们再看一个平方阶复杂度的算法——即便它是暴力的，其效率依然是可接受的，其提供的数据的自相似程度是足够高的。当现有资源——在早期阶段——不允许一个“优雅”的解决方案时，这个暴力算法亦多有裨益。

其他可以藉MEMulator™实现的操作包括平滑处理(抹掉那些凹凸不平的体素),晶体键合(旋转、平移、和两个八叉树的合并)、裁剪、连接和等值面提取。最后两个操作将分别在第5节和第6节介绍。共享八叉树与结果匹配算法“增益其所不能”。

5 等值面提取和可视化

我们描述一个快速的等值面提取算法，那就是以共享八叉树作为输入和输出的splat层次树，以资大规模、交互式的可视化。

5.1介绍和以前的工作

等值面提取是一种用于可视化的常见技术，一般做法是，访问所有体素间的接口，用三角形拟合表面[8]。即使对于中等大小的数据集，这一做法也导致了异常密集的网格(见图5.1)。这些网格不能显示交互帧频，并且一般的图形硬件还不能显示如此复杂的网格。

为了减少三角形网格，研究者们业已做了大量的工作[15]。然而,这些技术往往需要大量的计算。作为一个例子,图5.1所示的网格简化大约24万个三角形,但是这个过程花了65秒。

最近有了等值面提取技术的报告[17]。这种技术以一个八叉树组织输入数据，然后构造一个多边形等值面，在数秒之内生成了数十万个三角形，并进行实时可视化，所使用的最大数据集达到了512^3。

点渲染系统[12]亦于最近被提出,它允许呈现大规模交互性高分辨率数据集。一个分层的splat树从茂密的三角形网格中萌蘖，这个splat树可以在交互式帧频实现分层视图剔除和多分辨率渲染。使用这种技术对体积数据进行可视化和等值面提取，这一操作需要进行预处理，即转换为splat树。

5.2构建splat树

我们直接从共享八叉树建立一个分层的splat树。每个节点存储一个splat，splat有三个参数:位置、半径,和法向量，半径业已被选定，以资splat包络子树表征的曲面。

自底向上构建splat树。一个体素及其七个邻居(即负轴上的面、边和顶点数据集合)形成一个立方体。我们沿着每个立方体的边缘确定交点——标量场的边疆。然后我们利用最小二乘法拟合中心、半径和法向量这三个splat参数，由是建立splat树。注意，两个相邻的splat代表相同的表面无缝衔接[12]。然而,若在缩放或高分辨率情形下，这些重叠是可见的。

在内部的节点，splat参数是各孩子节点splat参数的加权平均，内部节点的法锥面可以用来刻画剔除过程[12]。我们还开发了减少splat树大小的技术，那就是如果一个特定的内部节点在用户指定的误差区间内可被判定为与其孩子节点共面，它便将这些相同的信息集中存储。因此,内存需求可能通过消弭孩子节点实现。

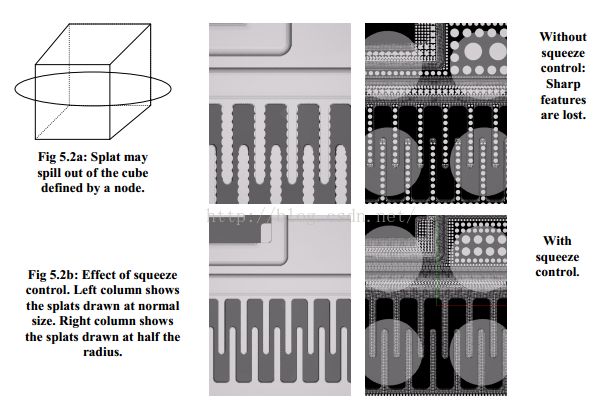
一个特定的splat可能溢出 (图5.2 a)，也可能“泯然众节点”，导致表面钝化失真(图5.2 b)。因此，我们要限制压缩的力度，防止两个相邻节点被混淆的情形。

图5.2

5.3共享网格节点和匹配结果

我们使用第2节中描述的技术拟合，并将一个splat树节点缓存以资反复引用。如果输入是一个共享八叉树，我们可以利用结果匹配加速处理。注意，splat参数可以从当前节点及其七个邻居中求得，而我们缓存的是一个八叉树节点。图5.3是通过结果匹配加速的情形。

图5.3

5.4可视化

使用与[12]中相同的渲染技术，精细的剔除是很容易实现的。此外,因为我们有一个分层的数据结构、多分辨率渲染降低了精细剔除的门槛。因此,当用户在虚拟环境中操作时(缩放,平移等)，交互式帧频以低分辨率图形作为呈现的开始。当用户停止移动镜头，呈现对象逐步改进。

6 连接

把我们得到的所有体素连接起来，将允许我们更加灵活的对模型进行各种组合，我们将描述我们如何推广标准连接算法，并将我们的结果匹配算法添加进去，连接性能将明显提升。

6.1标准连接算法

我们基于二维情形描述了这一算法，将其推广到三维情形是很简单的。我们考虑两个相邻像素共享一个连接边缘。我们首先分配一个独特的组件标签(等价于每个像素类)。然后从左到右、自底向上遍历像素，如果像素与其左边像素的数值相等，就将它们合并，这将使得数据结构更加灵活[1]。一旦所有的像素都被访问，就给每一个像素分配一个连接组件的值。

6.2结果匹配

上述算法需要访问每一个数据集内的像素,使得计算成本高昂。现在我们来描述如何使用结果匹配减少计算成本。因为我们是在二维情形下描述算法，我们假设一株共享四叉树来表征图形，节点类型记为T1。生成另一个共享四叉树，每个节点兼具连接组件标签信息和标准的像素信息(T1型)，节点类型记作T2。

我们需要遍历此树，当我们访问一个节点时,我们应该确认已访问了它更低层次的邻居节点，遍历顺序如图6.1所示。

设我们正处于一个T1型节点N，对所有的孩子节点计算连接组件信息。现有四个T2型节点：C1,C2,C3,C4。创建一个新的T2类型的节点M，并分配C1,C2,C3和C4作为其孩子节点。缓存处理结果，如果重逢节点M，结果可以获得直接从缓存求取。

警告，结果匹配只有当节点的所有组件最简后才能实现。参见图6.2。左边的图代表结果存储在哈希表中。白色的节点是T1型的“当前节点”，斜向和垂直条纹节点是当前节点的低层邻居。横向条纹节点是哈希表的值。条纹节点与组件信息相联系，以T2型存储。请注意，组件3不与任何低层邻居(对角线和垂直条纹)相连。现在,如果同样的组合在不同的树被发现(如右图),组件1和5将被准确合并。注意,对角线和垂直条纹节点——它们是T2型的——已经被求取。组件1和5存储于原始节点，然而,组件3并非如是。由于使用了结果匹配，我们可以将标准过程加速1到2倍。

7 结论和未来的工作

共享八叉树数据结构与结果匹配算法相结合，促进了快速、准确和鲁棒性强的几何建模操作，尤其是在大规模数据的情形下简化了对体素的操作，并提高了准确度，亦使得实时可视化合成模型成为可能。

我们也将考虑如何达到更好的压缩和加速效果，并放宽共享八叉树的匹配要求。两个不完全相同的域也是可以匹配的。

我们相信通过使用共享八叉树，将允许那些应用程序以更低成本呈现更好效果，这亦将进一步体现几何法则的力量。

8. ACKNOWLEDGEMENTS

Much of this work was supported by NIST ATPgrant 70NANB1H3021. The work was performed at Zyvex Corporation which ispursuing IP protection in this and other areas.

 

9. REFERENCES

[1] Aho, A., Hopcroft, J., and Ullman, J. Data Structures and Algorithms.Addison-Wesley, Reading, 1983.

[2] Coventor. Inc. www.coventor.com

[3] Frisken, F., Perry, R. Kizamu: A System for Sculpting DigitalCharacters. SIGGRAPH 2001.

[4] Kaufman, A., Cohen, D. and Yagel, R. Volume Graphics. IEEE Computer,26(7): 51-64, 1993.

[5] Keyser, J., Krishnan, S. and Manocha, D. Efficient {B}-rep Generation ofLow-Degree Sculptured Solids Using Exact Arithmetic. Univ. of North CarolinaTR96-040, 1996.

[6] Kolb, A. and John, L. Volumetric Model Repair for Virtual RealityApplications. Proceedings of EUROGRAPHICS 2001

[7] Kaufman, A. and Shimony, E. 3D scan-conversion algorithms forvoxel-based graphics. Proceedings of 1986 Workshop on Interactive 3D Graphics,Chapel Hill, North Carolina: 45-75, Oct 1986

[8] Lorensen, W. and Cline, H. Marching Cubes: A High Resolution 3D SurfaceConstruction Algorithm. Computer Graphics. 21(3):163-169, 1987

[9] MemsCap. www.memscap.com

[10] Noh, W. and Woodward, P. Simple LineInterface Calculation. Proc., Fifth Int. Conf. on Fluid Dynamics: 1976.

[11] Gosper, R. Exploiting Regularities inlarge cellular spaces. Physica 10D: 75-80, 1984

[12] Rusinkiewicz, S. and Levoy, M. QSplat:A Multiresolution Point Rendering System for Large Meshes. Computer Graphics(SIGGRAPH ’00): 353-358, 2000.

[13] Samet, H. The Design and Analysis ofSpatial Data Structures. Addison-Wesley, Reading, 1990.

[14] Srámek, M. and Kaufman, A. Alias-FreeVoxelization of Geometric Objects. IEEE Transactions on Visualization andComputer Graphics 3(6): 236-252, 2000.

[15] Schroeder, W., Zarge, J., andLorensen, W. Decimation of Triangle Meshes. Computer Graphics (SIGGRAPH ’92).26(2):65-70, 1992.

[16] Tan, Z., Furmanczyk, M., Turowski, M.and Przekwas A. J., CFD-Micromesh: A Fast Geometrical Modeling and MeshGeneration Tool for 3D Microsystem Simulations. Proc. of the MSM, March, 2000.

[17] Tao, J., Losasso, F., Schaefer, S. andWarren J. Dual Contouring of Hermite Data. ACM Transactions on Graphcs(SIGGRAPH’02). 21(3):339-346, 2002.

[18] Udeshi, T. and Parker, E. MEMulator: Afast and accurate Geometric Modeling, Visualization and Mesh Generation Toolfor 3D MEMS Design and Simulation. Technical Proceedings of the 2003Nanotechnology Conference and Trade Show, Vol. 2, Pg. 480-484.

[19] Wood, Z., Hoppe, H., Desburn, M. andSchroder P. Isosurface Topology Simplification. Microsoft Technical ReportMSR-TR-2002-28. 2002.

[20] Yarberry, V. Meeting the MEMS‘Design-to-Analysis' Challenge: The SUMMIT® V Design Tool Environment.Proceedings of ASME International Mechanical Engineering Congress &Exposition, Nov. 2002.