6.算法之二分查找与二叉排序树
(一)复杂度
log2n
(二)二分查找代码
//递归实现
bool binary_search(vector<int> &sort_array,int beg,int end,int target)
{
if(beg>end)
return false;
int mid=(end-beg)/2+beg;//迭代器时使用
//int mid=(beg+end)/2;
if(target==sort_array[mid]){
return true;
}else if(target>sort_array[mid]){
return binary_search(sort_array,mid+1,end,target);
}else if(target<sort_array[mid]){
return binary_search(sort_array,beg,mid-1,target);
}
}
//循环实现
bool binary_search(vector<int> &sort_array,int target)
{
int beg=0;
int end=sort_array.size()-1;
while(beg<=end){
int mid=(end-beg)/2+beg;//迭代器时使用
//int mid=(beg+end)/2;
if(target==sort_array[mid]){
return true;
}else if(target>sort_array[mid]){
beg=mid+1;
}else if(target<sort_array[mid]){
end=mid-1;
}
}
return false;
}
35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
输入: [1,3,5,6], 5
输出: 2
示例 2:
输入: [1,3,5,6], 2
输出: 1
示例 3:
输入: [1,3,5,6], 7
输出: 4
示例 4:
输入: [1,3,5,6], 0
输出: 0
设插入的位置为index: 给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。 思考: ①查找区间左端点时,增加如下限制条件: 假设按照升序排序的数组在预先未知的某个点上进行了旋转。 序列化是将数据结构或对象转换为一系列位的过程,以便它可以存储在文件或内存缓冲区中,或通过网络连接链路传输,以便稍后在同一个或另一个计算机环境中重建。 用处:压缩,将二叉查找树压缩写入一个文件 二叉查找树前序遍历与复原<只有前序可以> 给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
如果target>=num[mid],那么index=mid;
如果targetclass Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int beg=0;
int end=nums.size()-1;
int index=-1;
while(index==-1){
int mid=beg+(end-beg)/2;//迭代器时使用
if(target==nums[mid]){
index=mid;
}else if(target>nums[mid]){
if(mid==nums.size()-1||target<nums[mid+1])
index=mid+1;
beg=mid+1;
}else if(target<nums[mid]){
if(mid==0||target>nums[mid-1])
index=mid;
end=mid-1;
}
}
return index;
}
};
34. 在排序数组中查找元素的第一个和最后一个位置
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值,返回 [-1, -1]。
示例 1:
输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]
示例 2:
输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]
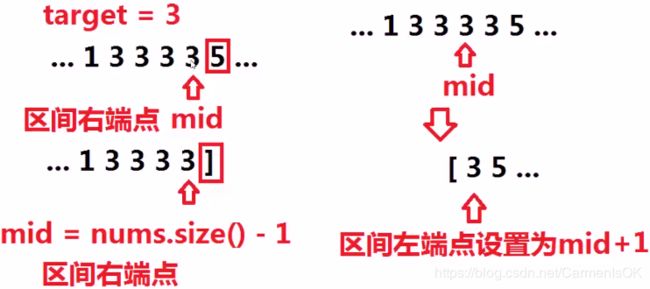
1.是否可以直接通过二分查找,很容易同时求出目标target所在区间的左右端点?
2.若无法同时求出区间的左右端点,将对目标的target的二分查找增加怎样的限制条件,就可分别求出目标target所在的区间左端点与右端点?
当target=num[mid]时,若此时mid=0或者nums[mid-1]
②查找区间右端点时,增加如下限制条件:
当target=num[mid]时,若此时mid=nums.size()-1或者nums[mid+1]>target,则说明mid即为区间右端点,返回;否则设置区间左端点为mid+1。
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
vector<int> res(2,-1);
res[0]=left_bound(nums,target);
res[1]=right_bound(nums,target);
return res;
}
private:
int left_bound(vector<int>& nums, int target)
{
int beg=0;
int end=nums.size()-1;
int mid=-1;
while(beg<=end)
{
mid=(beg+end)/2;
if(target==nums[mid])
{
if(mid==0||nums[mid-1]<target){
return mid;
}
end=mid-1;
}else if(target<nums[mid]){
end=mid-1;
}else if(target>nums[mid]){
beg=mid+1;
}
}
return -1;
}
int right_bound(vector<int>& nums, int target)
{
int beg=0;
int end=nums.size()-1;
int mid=-1;
while(beg<=end)
{
mid=(beg+end)/2;
if(target==nums[mid])
{
if(mid==nums.size()-1||nums[mid+1]>target){
return mid;
}
beg=mid+1;
}else if(target<nums[mid]){
end=mid-1;
}else if(target>nums[mid]){
beg=mid+1;
}
}
return -1;
}
};
33. 搜索旋转排序数组
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。
示例 1:
输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4
示例 2:
输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1



class Solution {
public:
int search(vector<int>& nums, int target) {
int beg=0;
int end=nums.size()-1;
while(beg<=end){
int mid=(beg+end)/2;
if(target==nums[mid])
return mid;
else if(target<nums[mid]){
if(nums[beg]<nums[mid]){
if(target>=nums[beg]){
end=mid-1;
}else{
beg=mid+1;
}
}
else if(nums[beg]>nums[mid]){
end=mid-1;
}
else if(nums[beg]==nums[mid]){
beg=mid+1;
}
}
else if(target>nums[mid]){
if(nums[beg]<nums[mid]){
beg=mid+1;
}
else if(nums[beg]>nums[mid]){
if(target>=nums[beg]){
end=mid-1;
}else{
beg=mid+1;
}
}
else if(nums[beg]==nums[mid]){
end=mid+1;
}
}
}
return -1;
}
};
449. 序列化和反序列化二叉搜索树
设计一个算法来序列化和反序列化二叉搜索树。 对序列化/反序列化算法的工作方式没有限制。 您只需确保二叉搜索树可以序列化为字符串,并且可以将该字符串反序列化为最初的二叉搜索树。
编码的字符串应尽可能紧凑。
注意:不要使用类成员/全局/静态变量来存储状态。 你的序列化和反序列化算法应该是无状态的。
网络传输,进程通信->编码解码/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
string data;
BST_preorder(root,data);
return data;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
if(data.length()==0)
return NULL;
vector<TreeNode *> node_vec;
int val=0;
for(int i=0;i<data.length();i++)
{
if(data[i]=='#')
{
node_vec.push_back(new TreeNode(val));
val=0;
}else
{
val=val*10+data[i]-'0';
}
}
for(int i=1;i<node_vec.size();i++)
{
BST_insert(node_vec[0],node_vec[i]);
}
return node_vec[0];
}
private:
void change_int_to_string(int val,string &str_val)
{
string tmp;
while(val)
{
tmp+=(val%10+'0');
val=val/10;
}
for(int i=tmp.length()-1;i>=0;i--)
{
str_val+=tmp[i];
}
str_val+='#';
}
void BST_preorder(TreeNode *node,string &data)
{
if(!node)
return;
string str_val;
change_int_to_string(node->val,str_val);
data+=str_val;
BST_preorder(node->left,data);
BST_preorder(node->right,data);
}
void BST_insert(TreeNode *node,TreeNode *insert_node){
if(insert_node->val<node->val){
if(node->left){
BST_insert(node->left,insert_node);
}
else{
node->left=insert_node;
}
}
else{
if(node->right){
BST_insert(node->right,insert_node);
}
else{
node->right=insert_node;
}
}
}
};
// Your Codec object will be instantiated and called as such:
// Codec codec;
// codec.deserialize(codec.serialize(root));
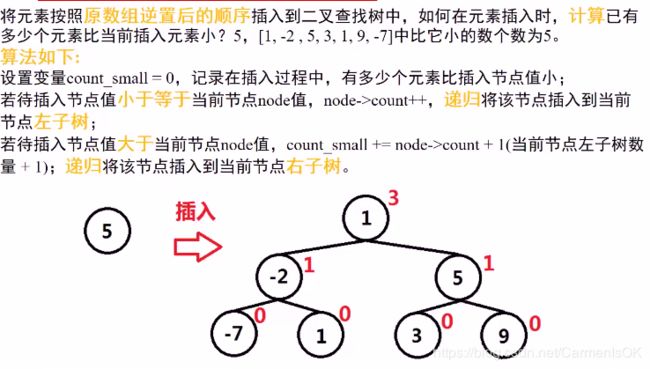
315. 计算右侧小于当前元素的个数
示例:
输入: [5,2,6,1]
输出: [2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1).
2 的右侧仅有 1 个更小的元素 (1).
6 的右侧有 1 个更小的元素 (1).
1 的右侧有 0 个更小的元素.


struct BSTNode{
int val;
int count;
BSTNode *left;
BSTNode *right;
BSTNode(int x):val(x),left(NULL),right(NULL),count(0){}
};
class Solution {
public:
vector<int> countSmaller(vector<int>& nums) {
vector<int> count;//向后插入过程中,比当前节点值小的
vector<BSTNode *>node_vec;//创建的二叉查找树结点池
vector<int> result;//最终逆序数数组
for(int i=nums.size()-1;i>=0;i--)
{
node_vec.push_back(new BSTNode(nums[i]));
}//从后向前的顺序创建二叉查找树结点
count.push_back(0);//第一个结点count_small=0
for(int i=1;i<node_vec.size();i++)
{
int count_small=0;
BST_insert(node_vec[0],node_vec[i],count_small);
count.push_back(count_small);
}
for(int i=node_vec.size()-1;i>=0;i--){
delete node_vec[i];
result.push_back(count[i]);
}
return result;
}
private:
void BST_insert(BSTNode *node,BSTNode *insert_node,int &count_small){
if(insert_node->val<=node->val){
node->count++;
if(node->left){
BST_insert(node->left,insert_node,count_small);
}
else{
node->left=insert_node;
}
}
else{
count_small+=node->count+1;
if(node->right){
BST_insert(node->right,insert_node,count_small);
}
else{
node->right=insert_node;
}
}
}
};