基于HMM+Viterbi算法的词性标注 Python
1 概述
隐含马尔可夫模型(HMM)被认为是解决大多数自然语言处理问题最快速、有效的方法; 20世纪70年代被应用在语音处理上,后被广泛应用在汉 语自动分词、词性标注、统计机器翻译等方面。 本次文章将介绍基于HMM和Viterbi算法进行词性标注。
2 理论描述
2.1 HMM五元组
HMM是一个五元组(O,S, O 0 O_0 O0,A,B):
- O:{ o 1 o_1 o1… o t o_t ot}是状态集合, 也称为观测序列 ;
- S:{ s 1 s_1 s1… s v s_v sv}是一组输出结果,也称隐序列 ;
- a i j a_{ij} aij=P( s j s_j sj| s i s_i si): 转移概率分布 ;
- b i j b_{ij} bij=P( o j o_j oj| s i s_i si):发射概率分布 ;
- O 0 O_0 O0是初始状态,有些还有终止状态。
HMM可以用于估算隐藏于表面事件背后的事件的概率。 在词性标注中,词串可视为可观察序列,词的词性可视为隐序列。
2.2 HMM三个基本问题
- 估计问题:给定一个隐马尔科夫模型M=(A,B),如何有效计算某个观测序列O出现的概率,即计算P(O|M) (A表示转移概率,B表示发射概率) 。
- 解码问题:给定一个观测序列O和一个HMM模型M,寻找最好的隐序列Q以便最好的解释观测值 。
- 学习问题:依据给定的观测序列O以及HMM模型中的状态集合,学习最佳HMM参数模型A和B。
我们所讨论的词性标注问题即是HMM中的解码问题。
2.3 Viterbi算法
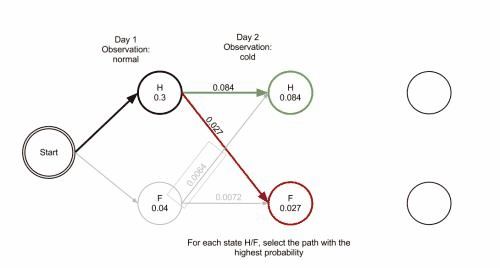
Viterbi算法实际上是最优路径算法的一种。在HMM的解码问题中,我们可以使用穷举法把所有可能的隐序列的概率都计算出来,这样最优解自然就出来了,但是缺点也很明显,即计算量太大。Viterbi算法的主要思想是寻找局部最优路径,即寻找所有序列中在t时刻以状态j终止的最大概率,所对应的路径为部分最优路径。依据最后一个时刻中概率最高的状态,通过回溯找其路径中的上一个最大部分最优路径,从而找到整个最优路径,而不用穷举所有的状态。这样就比计算整个的排列组合的次数要小得多。穷举的时间复杂度为O( m n m^n mn),而Viterbi是多次对链中的一个小分布穷举,时间复杂度为O(m*n)。 下面是wiki百科给出的乡村诊所例子的解释图:
3 算法描述
- 构造两个矩阵,max_p每一列为当前观测序列不同隐状态的最大概率;path每一行存储上max_p对应列的路径,用于回溯;
- 初始化max_p第1个观测节点不同隐状态的最大概率并初始化path从各个隐状态出发;
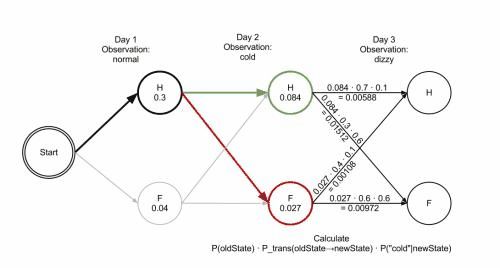
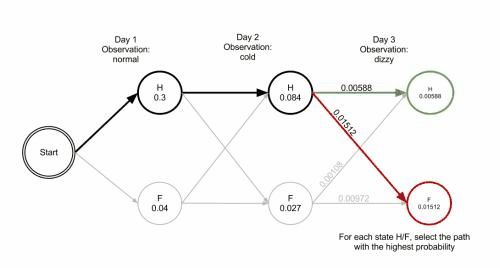
- 遍历第1项后的每一个观测序列,计算其不同隐状态的最大概率,计算公式为 ν t ( j ) = m a x ( v t − 1 ( i ) × a i j ) × b j ( o t ) ν_t (j) = max(v_{t−1}(i)×a_{ij})×b_j (o_t ) νt(j)=max(vt−1(i)×aij)×bj(ot);
- 记录最大概率及路径,用新的路径覆盖之前的路径;
- 到达最后一个观测节点,比较并返回概率最大的路径,从path中取出。
4 详例描述
输入:‘The’, ‘bear’, ‘is’, ‘on’, ‘the’, ‘move’, '.
隐状态:‘AT’, ‘BEZ’, ‘IN’, ‘NN’, ‘VB’, ‘PERIOD’
输出:The/AT bear/NN is/BEZ on/IN the/AT move/NN ./PERIOD
初始概率:语料库中各词性出现的占比
AT BEZ IN NN VB PERIOD 0.2 0.1 0.1 0.2 0.3 0.1
转移概率矩阵:由当前词性 a i a_i ai转移到下一个词性 a j a_j aj的概率
AT(第二个标记) BEZ IN NN VB PERIOD AT(第一个标记) 1 48659 \frac{1}{48659} 486591 1 48659 \frac{1}{48659} 486591 1 48659 \frac{1}{48659} 486591 48636 48659 \frac{48636}{48659} 4865948636 1 48659 \frac{1}{48659} 486591 19 48659 \frac{19}{48659} 4865919 BEZ 1937 2590 \frac{1937}{2590} 25901937 1 2590 \frac{1}{2590} 25901 426 2590 \frac{426}{2590} 2590426 187 2590 \frac{187}{2590} 2590187 1 2590 \frac{1}{2590} 25901 38 2590 \frac{38}{2590} 259038 IN 43322 62148 \frac{43322}{62148} 6214843322 1 62148 \frac{1}{62148} 621481 1325 62148 \frac{1325}{62148} 621481325 17314 62148 \frac{17314}{62148} 6214817314 1 62148 \frac{1}{62148} 621481 185 62148 \frac{185}{62148} 62148185 NN 1067 81036 \frac{1067}{81036} 810361067 3720 81036 \frac{3720}{81036} 810363720 42470 81036 \frac{42470}{81036} 8103642470 11773 81036 \frac{11773}{81036} 8103611773 614 81036 \frac{614}{81036} 81036614 21392 81036 \frac{21392}{81036} 8103621392 VB 6082 14009 \frac{6082}{14009} 140096082 42 14009 \frac{42}{14009} 1400942 4758 14009 \frac{4758}{14009} 140094758 1476 14009 \frac{1476}{14009} 140091476 129 14009 \frac{129}{14009} 14009129 1522 14009 \frac{1522}{14009} 140091522 PERIOD 8016 15031 \frac{8016}{15031} 150318016 75 15031 \frac{75}{15031} 1503175 4656 15031 \frac{4656}{15031} 150314656 1329 15031 \frac{1329}{15031} 150311329 954 15031 \frac{954}{15031} 15031954 1 15031 \frac{1}{15031} 150311
发射概率矩阵:隐状态到观测状态的概率,即 t h e ( A T ) 数 总 A T 数 \frac{the(AT)数}{总AT数} 总AT数the(AT)数(下表只展示了需要的观测序列)
The bear is on the move . AT 69016 69023 \frac{69016}{69023} 6902369016 1 69023 \frac{1}{69023} 690231 1 69023 \frac{1}{69023} 690231 1 69023 \frac{1}{69023} 690231 69016 69023 \frac{69016}{69023} 6902369016 1 69023 \frac{1}{69023} 690231 1 69023 \frac{1}{69023} 690231 BEZ 1 10072 \frac{1}{10072} 100721 1 10072 \frac{1}{10072} 100721 10065 10072 \frac{10065}{10072} 1007210065 1 10072 \frac{1}{10072} 100721 1 10072 \frac{1}{10072} 100721 1 10072 \frac{1}{10072} 100721 1 10072 \frac{1}{10072} 100721 IN 1 5491 \frac{1}{5491} 54911 1 5491 \frac{1}{5491} 54911 1 5491 \frac{1}{5491} 54911 5484 5491 \frac{5484}{5491} 54915484 1 5491 \frac{1}{5491} 54911 1 5491 \frac{1}{5491} 54911 1 5491 \frac{1}{5491} 54911 NN 1 543 \frac{1}{543} 5431 10 543 \frac{10}{543} 54310 1 543 \frac{1}{543} 5431 1 543 \frac{1}{543} 5431 1 543 \frac{1}{543} 5431 36 543 \frac{36}{543} 54336 1 543 \frac{1}{543} 5431 VB 1 187 \frac{1}{187} 1871 43 187 \frac{43}{187} 18743 1 187 \frac{1}{187} 1871 1 187 \frac{1}{187} 1871 1 187 \frac{1}{187} 1871 133 187 \frac{133}{187} 187133 1 187 \frac{1}{187} 1871 PERIOD 1 48814 \frac{1}{48814} 488141 1 48814 \frac{1}{48814} 488141 1 48814 \frac{1}{48814} 488141 1 48814 \frac{1}{48814} 488141 1 48814 \frac{1}{48814} 488141 1 48814 \frac{1}{48814} 488141 48809 48814 \frac{48809}{48814} 4881448809
表中数据由Brwon语料库中的理想计数得来,为避免出现条件概率为0的情况,而使得整条路径概率为0,这里使用了加一法进行了数据平滑。
最大概率矩阵:
v 0 ( j ) = i n i t ( j ) × b j ( o 0 ) v_0(j)=init(j)×b_j(o_0) v0(j)=init(j)×bj(o0) (init为初始概率,b发射概率矩阵)
ν t ( j ) = m a x ( v t − 1 ( i ) × a i j ) × b j ( o t ) ν_t (j) = max(v_{t−1}(i)×a_{ij})×b_j (o_t ) νt(j)=max(vt−1(i)×aij)×bj(ot) (a为转移概率矩阵,b为发射概率矩阵)其中我们使用path在每个
t(时刻/index)更新并保存j(观测状态/词串)条路径取到最大概率时的i(隐状态/词性),用于回溯。
The bear is on the move . AT 1.99979717e-01 1.00907884e-08 7.02220304e-10 1.82969972e-09 1.93346773e-05 5.75678377e-15 2.44414441e-13 BEZ 9.92851469e-06 1.67872436e-09 1.68866614e-04 6.47333846e-12 1.02337555e-13 6.48663240e-14 5.83960534e-12 IN 1.82116190e-05 9.92305748e-08 3.51344866e-07 2.77395642e-05 1.07705259e-10 1.35838501e-12 1.22288915e-10 NN 3.68324125e-04 3.68112691e-03 9.84895399e-07 2.24535911e-08 1.42321352e-08 1.28125115e-06 3.42802191e-10 VB 1.60427807e-03 3.39694936e-06 1.49152164e-07 3.48660241e-10 2.38688156e-12 2.82607565e-10 5.19138262e-11 PERIOD 6.65291730e-06 1.15957619e-08 6.46496696e-08 1.64831327e-10 5.49359109e-12 5.02272586e-13 1.09829675e-06
path矩阵:用于回溯,每一行存储上max_p对应列的路径
第1个观测值:
[[0. 0. 0. 0. 0. 0. 0.]
[1. 0. 0. 0. 0. 0. 0.]
[2. 0. 0. 0. 0. 0. 0.]
[3. 0. 0. 0. 0. 0. 0.]
[4. 0. 0. 0. 0. 0. 0.]
[5. 0. 0. 0. 0. 0. 0.]]
第2个观测值:
[[4. 0. 0. 0. 0. 0. 0.]
[3. 1. 0. 0. 0. 0. 0.]
[4. 2. 0. 0. 0. 0. 0.]
[0. 3. 0. 0. 0. 0. 0.]
[4. 4. 0. 0. 0. 0. 0.]
[4. 5. 0. 0. 0. 0. 0.]]
第3个观测值:
[[0. 3. 0. 0. 0. 0. 0.]
[0. 3. 1. 0. 0. 0. 0.]
[0. 3. 2. 0. 0. 0. 0.]
[0. 3. 3. 0. 0. 0. 0.]
[0. 3. 4. 0. 0. 0. 0.]
[0. 3. 5. 0. 0. 0. 0.]]
第4个观测值:
[[0. 3. 1. 0. 0. 0. 0.]
[0. 3. 1. 1. 0. 0. 0.]
[0. 3. 1. 2. 0. 0. 0.]
[0. 3. 1. 3. 0. 0. 0.]
[0. 3. 1. 4. 0. 0. 0.]
[0. 3. 1. 5. 0. 0. 0.]]
第5个观测值:
[[0. 3. 1. 2. 0. 0. 0.]
[0. 3. 1. 3. 1. 0. 0.]
[0. 3. 1. 2. 2. 0. 0.]
[0. 3. 1. 2. 3. 0. 0.]
[0. 3. 1. 2. 4. 0. 0.]
[0. 3. 1. 2. 5. 0. 0.]]
第6个观测值:
[[0. 3. 1. 2. 0. 0. 0.]
[0. 3. 1. 2. 3. 1. 0.]
[0. 3. 1. 2. 3. 2. 0.]
[0. 3. 1. 2. 0. 3. 0.]
[0. 3. 1. 2. 0. 4. 0.]
[0. 3. 1. 2. 0. 5. 0.]]
第7个观测值:
[[0. 3. 1. 2. 0. 3. 0.]
[0. 3. 1. 2. 0. 3. 1.]
[0. 3. 1. 2. 0. 3. 2.]
[0. 3. 1. 2. 0. 3. 3.]
[0. 3. 1. 2. 0. 3. 4.]
[0. 3. 1. 2. 0. 3. 5.]]
5 实现代码
import numpy as np
def viterbi(obs_len, states_len, init_p, trans_p, emit_p):
"""
:param obs_len: 观测序列长度 int
:param states_len: 隐含序列长度 int
:param init_p:初始概率 list
:param trans_p:转移概率矩阵 np.ndarray
:param emit_p:发射概率矩阵 np.ndarray
:return:最佳路径 np.ndarray
"""
max_p = np.zeros((states_len, obs_len)) # max_p每一列为当前观测序列不同隐状态的最大概率
path = np.zeros((states_len, obs_len)) # path每一行存储上max_p对应列的路径
# 初始化max_p第1个观测节点不同隐状态的最大概率并初始化path从各个隐状态出发
for i in range(states_len):
max_p[i][0] = init_p[i] * emit_p[i][0]
path[i][0] = i
# 遍历第1项后的每一个观测序列,计算其不同隐状态的最大概率
for obs_index in range(1, obs_len):
new_path = np.zeros((states_len, obs_len))
# 遍历其每一个隐状态
for hid_index in range(states_len):
# 根据公式计算累计概率,得到该隐状态的最大概率
max_prob = -1
pre_state_index = 0
for i in range(states_len):
each_prob = max_p[i][obs_index - 1] * trans_p[i][hid_index] * emit_p[hid_index][obs_index]
if each_prob > max_prob:
max_prob = each_prob
pre_state_index = i
# 记录最大概率及路径
max_p[hid_index][obs_index] = max_prob
for m in range(obs_index):
# "继承"取到最大概率的隐状态之前的路径(从之前的path中取出某条路径)
new_path[hid_index][m] = path[pre_state_index][m]
new_path[hid_index][obs_index] = hid_index
# 更新路径
path = new_path
# 返回最大概率的路径
max_prob = -1
last_state_index = 0
for hid_index in range(states_len):
if max_p[hid_index][obs_len - 1] > max_prob:
max_prob = max_p[hid_index][obs_len - 1]
last_state_index = hid_index
return path[last_state_index]
if __name__ == '__main__':
hidden_state = ['AT', 'BEZ', 'IN', 'NN', 'VB', 'PERIOD'] # 隐状态
observation = ['The', 'bear', 'is', 'on', 'the', 'move', '.'] # 观测序列
# 初始状态
start_probability = [0.2, 0.1, 0.1, 0.2, 0.3, 0.1]
# 转移概率
transaction_probability = np.array(
[[1 / 48659, 1 / 48659, 1 / 48659, 48636 / 48659, 1 / 48659, 19 / 48659],
[1937 / 2590, 1 / 2590, 426 / 2590, 187 / 2590, 1 / 2590, 38 / 2590],
[43322 / 62148, 1 / 62148, 1325 / 62148, 17314 / 62148, 1 / 62148, 185 / 62148],
[1067 / 81036, 3720 / 81036, 42470 / 81036, 11773 / 81036, 614 / 81036, 21392 / 81036],
[6082 / 14009, 42 / 14009, 4758 / 14009, 1476 / 14009, 129 / 14009, 1522 / 14009],
[8016 / 15031, 75 / 15031, 4656 / 15031, 1329 / 15031, 954 / 15031, 1 / 15031]])
# 发射概率
emission_probability = np.array(
[[69016 / 69023, 1 / 69023, 1 / 69023, 1 / 69023, 69016 / 69023, 1 / 69023, 1 / 69023],
[1 / 10072, 1 / 10072, 10065 / 10072, 1 / 10072, 1 / 10072, 1 / 10072, 1 / 10072],
[1 / 5491, 1 / 5491, 1 / 5491, 5484 / 5491, 1 / 5491, 1 / 5491, 1 / 5491],
[1 / 543, 10 / 543, 1 / 543, 1 / 543, 1 / 543, 36 / 543, 1 / 543],
[1 / 187, 43 / 187, 1 / 187, 1 / 187, 1 / 187, 133 / 187, 1 / 187],
[1 / 15031, 1 / 15031, 1 / 15031, 1 / 15031, 1 / 15031, 1 / 15031, 48809 / 15031]])
result = viterbi(len(observation), len(hidden_state),
start_probability, transaction_probability, emission_probability)
tag_line = ''
for k in range(len(result)):
tag_line += observation[k] + "/" + hidden_state[int(result[k])] + ' '
print(tag_line)
6 基于人民日报语料库生成转移矩阵和发射矩阵
掌握了HMM和Viterbi算法的基本原理之后,我们可以来研究如何使用特定语料库通过HMM算法进行词性标注?
下一篇文章将详细介绍具体步骤及出现的问题。
基于特定语料库生成HMM转移概率分布和发射概率分布用于词性标注 Python