关于图像处理中的位图切割(Bit-pane Slicing)原理的自我见解
前段时间做过一道数字图像算法的课程一道题,就是有关位图分割算法的,但是当初没理解,我翻了几篇文章后把它弄明白了,所以我打算记录下我的想法,免得忘了。
题目:
Propose a set of intensity-slicing transformations capable of
producing all the individual bit planes of an 4-bit monochrome image.
(For example, a transformation function with the property T®=0 for r
in the range [0,7], and T®=15 for r in the range [8,15] produces an
image of the 4th bit plane in an 4-bit image.)
提出一组强度切片变换,能够产生4位单色图像的所有单个位平面。(例如,在[0,7]范围内具有属性T®=0的变换函数,在范围[8,15]中,T®=15表示r,则在4位图像中生成第4位平面的图像。)
几位灰度图像就是说每个像素用几位来表示的。当我们把图像像素的每位的值提取作为一层,即位图切割。
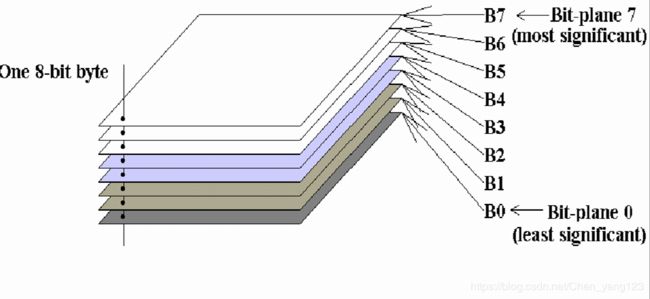
发现位数越高的层越接近原图像,即保留的信息就越多。如图:

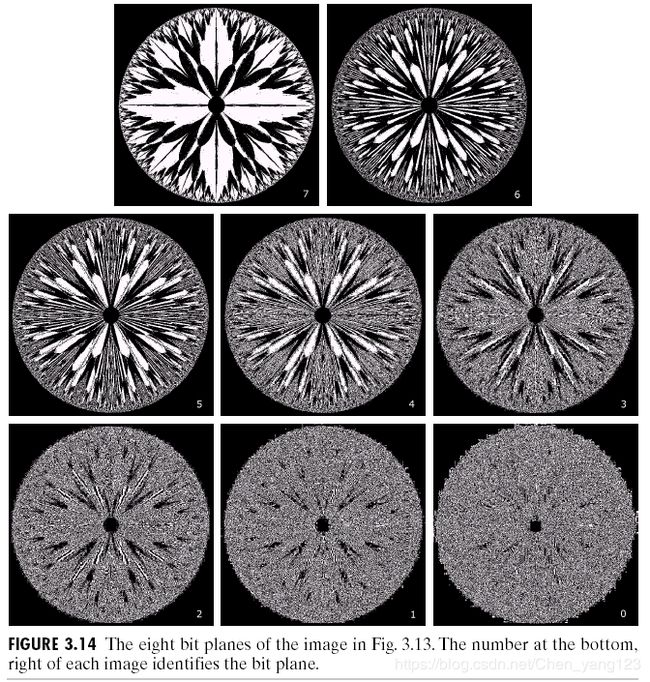
上面为原图,下面为效果图
但是这个原理是怎么实现呢?
以4位灰度图像为例。我们知道,每个像素值由4位二进制来表示,因此我们将4位图像根据位数分为4层。假如我们要提取第4层图像的信息,即最高位,就要检测每个像素的第4位的值,即0或1。当为1的时候,表示这个位保留着图像的信息,需要保留。当为0的时候,表示没有原图像信息。
我们写出第4位为0和第4位为1的像素值边界:
0 0 0 0 =0
0 1 1 1 =7
1 0 0 0 =8
1 1 1 1 =15
即像素值在[0,7]内的像素第4位都为0,因此我们将在这个范围内的像素赋值为0;像素值在[8,15]内的像素第4位都为1,赋值为1(也可以赋值为其它值,只要不为0和不超过15)。写成表达式为
( r 为 像 素 值 ) T ( r ) = { 0 , r ∈ [ 0 , 7 ] 1 , r ∈ [ 8 , 15 ] ( r为像素值)T(r)=\left\{ \begin{array}{c} 0 ,r∈[0,7] \\ \\ 1,r∈[8,15]\end{array}\right. (r为像素值)T(r)=⎩⎨⎧0,r∈[0,7]1,r∈[8,15]
如我们检测到一个像素的值为10(二进制为1 0 1 0),第4位为1,那我们可以将此像素的值赋为1。
那要将第2层的分割出来呢?写出二进制范围的边界
0 0 0 0 =0
0 0 0 1 =1
0 0 1 0 =2
1 1 1 1 =15
表达式为:
( r 为 像 素 值 。 ) T ( r ) = { 0 , r ∈ [ 0 , 1 ] 1 , r ∈ [ 2 , 15 ] ( r为像素值。)T(r)=\left\{ \begin{array}{c} 0 ,r∈[0,1] \\ \\ 1,r∈[2,15]\end{array}\right. (r为像素值。)T(r)=⎩⎨⎧0,r∈[0,1]1,r∈[2,15]
其它层类似。
对于代码实现和更详细的内容,可以参考
https://blog.csdn.net/ningyaliuhebei/article/details/17161701
有错误也欢迎指出!