前言
学习数据结构与算法对于工程师去理解和分析问题都是有帮助的。如果将来当我们面对较为复杂的问题,这些基础知识的积累可以帮助我们更好的优化解决思路。下面罗列在前端面试中经常撞见的几个问题吧。
Q1 判断一个单词是否是回文?
回文是指把相同的词汇或句子,在下文中调换位置或颠倒过来,产生首尾回环的情趣,叫做回文,也叫回环。比如 mamam redivider .
很多人拿到这样的题目非常容易想到用for 将字符串颠倒字母顺序然后匹配就行了。其实重要的考察的就是对于reverse的实现。其实我们可以利用现成的函数,将字符串转换成数组,这个思路很重要,我们可以拥有更多的自由度去进行字符串的一些操作。
function checkPalindrom(str) {
return str == str.split('').reverse().join('');
}
Q2 去掉一组整型数组重复的值
比如输入: [1,13,24,11,11,14,1,2]
输出: [1,13,24,11,14,2]
需要去掉重复的11 和 1 这两个元素。
这道问题出现在诸多的前端面试题中,主要考察个人对Object的使用,利用key来进行筛选。
/**
* unique an array
**/
let unique = function(arr) {
let hashTable = {};
let data = [];
for(let i=0,l=arr.length;i
Q3 统计一个字符串出现最多的字母
给出一段英文连续的英文字符窜,找出重复出现次数最多的字母
输入 : afjghdfraaaasdenas
输出 : a
前面出现过去重的算法,这里需要是统计重复次数。
function findMaxDuplicateChar(str) {
if(str.length == 1) {
return str;
}
let charObj = {};
for(let i=0;i= maxValue) {
maxChar = k;
maxValue = charObj[k];
}
}
return maxChar;
}
module.exports = findMaxDuplicateChar;
Q4 排序算法
如果抽到算法题目的话,应该大多都是比较开放的题目,不限定算法的实现,但是一定要求掌握其中的几种,所以冒泡排序,这种较为基础并且便于理解记忆的算法一定需要熟记于心。冒泡排序算法就是依次比较大小,小的的大的进行位置上的交换。
function bubbleSort(arr) {
for(let i = 0,l=arr.length;iarr[j]) {
let tem = arr[i];
arr[i] = arr[j];
arr[j] = tem;
}
}
}
return arr;
}
module.exports = bubbleSort;
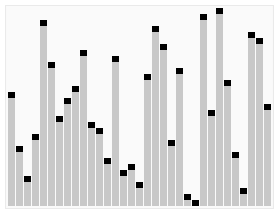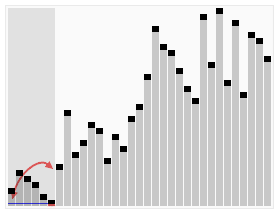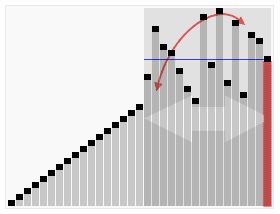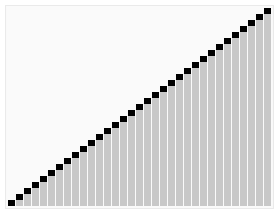
除了冒泡排序外,其实还有很多诸如 插入排序,快速排序,希尔排序等。每一种排序算法都有各自的特点。全部掌握也不需要,但是心底一定要熟悉几种算法。 比如快速排序,其效率很高,而其基本原理如图(来自wiki):
算法参考某个元素值,将小于它的值,放到左数组中,大于它的值的元素就放到右数组中,然后递归进行上一次左右数组的操作,返回合并的数组就是已经排好顺序的数组了。
function quickSort(arr) {
if(arr.length<=1) {
return arr;
}
let leftArr = [];
let rightArr = [];
let q = arr[0];
for(let i = 1,l=arr.length; iq) {
rightArr.push(arr[i]);
}else{
leftArr.push(arr[i]);
}
}
return [].concat(quickSort(leftArr),[q],quickSort(rightArr));
}
module.exports = quickSort;
安利大家一个学习的地址,通过动画演示算法的实现。
HTML5 Canvas Demo: Sorting Algorithms
Q5 不借助临时变量,进行两个整数的交换
输入 a = 2, b = 4 输出 a = 4, b =2
这种问题非常巧妙,需要大家跳出惯有的思维,利用 a , b进行置换。
主要是利用 + - 去进行运算,类似 a = a + ( b - a) 实际上等同于最后 的 a = b;
function swap(a , b) {
b = b - a;
a = a + b;
b = a - b;
return [a,b];
}
module.exports = swap;
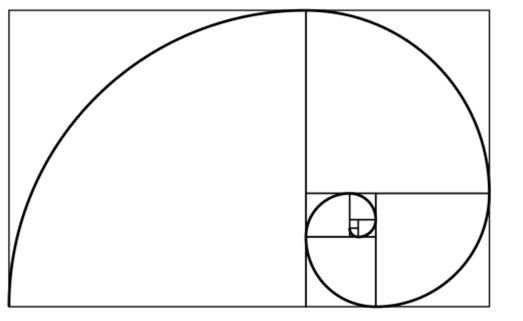
Q6 使用canvas 绘制一个有限度的斐波那契数列的曲线?
数列长度限定在9.
斐波那契数列,又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列主要考察递归的调用。我们一般都知道定义
fibo[i] = fibo[i-1]+fibo[i-2];
生成斐波那契数组的方法
function getFibonacci(n) {
var fibarr = [];
var i = 0;
while(i
剩余的工作就是利用canvas arc方法进行曲线绘制了
DEMO
Q7 找出下列正数组的最大差值比如:
输入 [10,5,11,7,8,9]
输出 6
这是通过一道题目去测试对于基本的数组的最大值的查找,很明显我们知道,最大差值肯定是一个数组中最大值与最小值的差。
function getMaxProfit(arr) {
var minPrice = arr[0];
var maxProfit = 0;
for (var i = 0; i < arr.length; i++) {
var currentPrice = arr[i];
minPrice = Math.min(minPrice, currentPrice);
var potentialProfit = currentPrice - minPrice;
maxProfit = Math.max(maxProfit, potentialProfit);
}
return maxProfit;
}
Q8 随机生成指定长度的字符串
实现一个算法,随机生成指制定长度的字符窜。
比如给定 长度 8 输出 4ldkfg9j
function randomString(n) {
let str = 'abcdefghijklmnopqrstuvwxyz9876543210';
let tmp = '',
i = 0,
l = str.length;
for (i = 0; i < n; i++) {
tmp += str.charAt(Math.floor(Math.random() * l));
}
return tmp;
}
module.exports = randomString;
Q9 实现类似getElementsByClassName 的功能
自己实现一个函数,查找某个DOM节点下面的包含某个class的所有DOM节点?不允许使用原生提供的 getElementsByClassName querySelectorAll 等原生提供DOM查找函数。
function queryClassName(node, name) {
var starts = '(^|[ \n\r\t\f])',
ends = '([ \n\r\t\f]|$)';
var array = [],
regex = new RegExp(starts + name + ends),
elements = node.getElementsByTagName("*"),
length = elements.length,
i = 0,
element;
while (i < length) {
element = elements[i];
if (regex.test(element.className)) {
array.push(element);
}
i += 1;
}
return array;
}
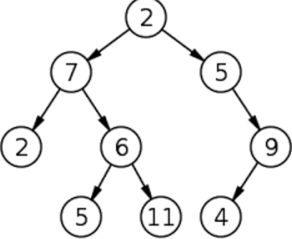
Q10 使用JS 实现二叉查找树(Binary Search Tree)
一般叫全部写完的概率比较少,但是重点考察你对它的理解和一些基本特点的实现。 二叉查找树,也称二叉搜索树、有序二叉树(英语:ordered binary tree)是指一棵空树或者具有下列性质的二叉树:
- 任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为O(log n)。二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、multiset、关联数组等。
在写的时候需要足够理解二叉搜素树的特点,需要先设定好每个节点的数据结构
class Node {
constructor(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
}
}
树是有节点构成,由根节点逐渐延生到各个子节点,因此它具备基本的结构就是具备一个根节点,具备添加,查找和删除节点的方法.
class BinarySearchTree {
constructor() {
this.root = null;
}
insert(data) {
let n = new Node(data, null, null);
if (!this.root) {
return this.root = n;
}
let currentNode = this.root;
let parent = null;
while (1) {
parent = currentNode;
if (data < currentNode.data) {
currentNode = currentNode.left;
if (currentNode === null) {
parent.left = n;
break;
}
} else {
currentNode = currentNode.right;
if (currentNode === null) {
parent.right = n;
break;
}
}
}
}
remove(data) {
this.root = this.removeNode(this.root, data)
}
removeNode(node, data) {
if (node == null) {
return null;
}
if (data == node.data) {
// no children node
if (node.left == null && node.right == null) {
return null;
}
if (node.left == null) {
return node.right;
}
if (node.right == null) {
return node.left;
}
let getSmallest = function(node) {
if(node.left === null && node.right == null) {
return node;
}
if(node.left != null) {
return node.left;
}
if(node.right !== null) {
return getSmallest(node.right);
}
}
let temNode = getSmallest(node.right);
node.data = temNode.data;
node.right = this.removeNode(temNode.right,temNode.data);
return node;
} else if (data < node.data) {
node.left = this.removeNode(node.left,data);
return node;
} else {
node.right = this.removeNode(node.right,data);
return node;
}
}
find(data) {
var current = this.root;
while (current != null) {
if (data == current.data) {
break;
}
if (data < current.data) {
current = current.left;
} else {
current = current.right
}
}
return current.data;
}
}
module.exports = BinarySearchTree;
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作能带来一定的帮助,如果有疑问大家可以留言交流。