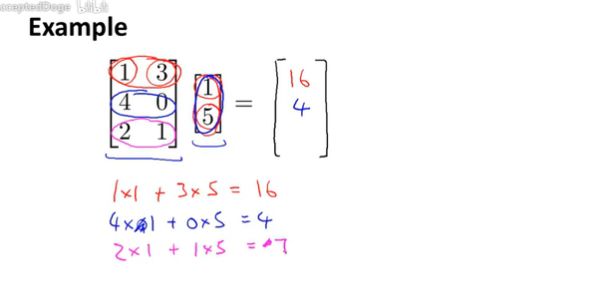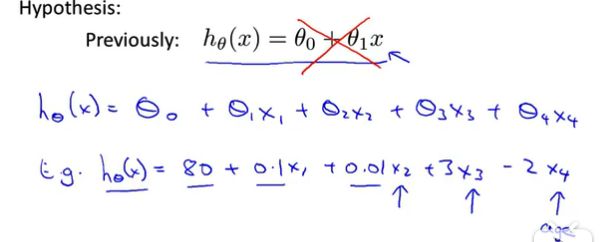本笔记是根据吴恩达教授开设的 Maching Learning 的公开课学习记录。
一、矩阵和向量
矩阵和向量(Matrices and Vectors)是如何计算的?
二、矩阵矩阵相乘
矩阵矩阵相乘(Matrix-matrix multiplication)
矩阵与矩阵的乘法运算
矩阵计算公式:
矩阵相乘,两个矩阵只有当左边的矩阵的行数等于右边矩阵的列数时,两个矩阵才可以进行矩阵的乘法运算。
示例,可以将另一个矩阵拆为向量运算:
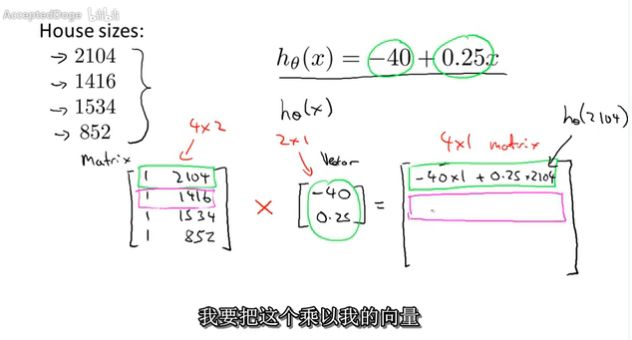
将实际问题转为矩阵计算处理:
三、矩阵运算特性
矩阵运算示例(Matrix multiplication properties)
A X B ≠ B X A
四、矩阵的逆运算和转置
逆运算和转置(inverse and transpose)
五、线性回归
线性回归与多变量(Linear Regression with multiple variables)
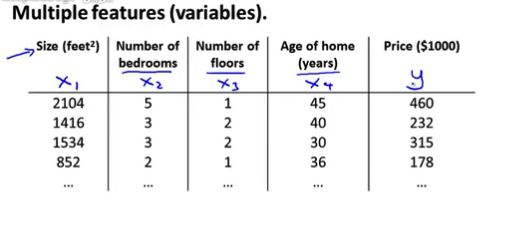
Multiple features
多变量特征(Multiple features)
Gradient Descent
梯度下降 Gradient Descent
六、Octave 学习
简介
Octave是一种编程语言,旨在解决线性和非线性的数值计算问题。Octave为GNU项目下的开源软件,早期版本为命令行交互方式,4.0.0版本发布基于QT编写的GUI交互界面。Octave语法与Matlab语法非常接近,可以很容易的将matlab程序移植到Octave。同时与C++,QT等接口较Matlab更加方便。
Octave是一种很好的原始语言(prototyping language),使用Octave你能快速地实现你的算法,剩下的事情,你只需要进行大规模的资源配置,你只用再花时间用C++或Java这些语言把算法重新实现就行了。开发项目的时间是很宝贵的,机器学习的时间也是很宝贵的。所以,如果你能让你的学习算法在Octave上快速的实现,基本的想法实现以后,再用C++或者Java去改写,这样你就能节省出大量的时间。
据我所见,人们使用最多的用于机器学习的原始语言是Octave、MATLAB、Python、NumPy 和R。
安装
windows 安装很简单,只需要去官网下载安装包解压安装即可,下面讲下怎么在Mac 上安装。
使用Homebrew安装Octave
Homebrew是一个包管理器,用于在Mac上安装一些OS X没有的UNIX工具(比如著名的wget)。它会将软件包安装到独立目录,并将其文件软链接至 /usr/local 。完全基于git 和 ruby,所以自由修改的同时你仍可以轻松撤销你的变更或与上游更新合并。
首先确认Mac已安装Xcode、Command Line Tool。安装Command Line Tool:
xcode-select --install然后把下面的代码粘贴到Terminal中执行安装Homebrew。
/usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)"Homebrew常用命令:
brew search/install/upgrade/info/deps/remove python3
brew list/outdated/update/Octave安装
输入以下命令安装Octave:
brew tap homebrew/science
brew update && brew upgrade
brew install octave安装完成可看到提示该GUI展示所基于框架的设置,默认为QT框架。
setenv('GNUTERM','qt') # Requires QT; install gnuplot --with-qt
setenv('GNUTERM','x11') # Requires XQuartz; install gnuplot --with-x11
setenv('GNUTERM','wxt') # Requires wxmac; install gnuplot --with-wxmac
setenv('GNUTERM','aqua') # Requires AquaTerm; install gnuplot --with-aquatermOctave无界面启动及配置
输入以下命令进行Octave无界面启动:
octave --no-guioctave:1> a = 3
a = 3
octave:2> 5 + 8
ans = 13
octave:3> A = [1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
octave:4>默认使用plot命令就会出现warning,使用如下配置可解决当前octave的问题。
octave:1> graphics_toolkit
ans = qt
octave:2> x=linspace(-10,10);
octave:3> plot(x,sin(x));
warning: opengl_renderer: Error 1286 occurred in init_gl_context
warning: called from
plot at line 223 column 10
octave:4> graphics_toolkit('gnuplot')
octave:5> plot(x,sin(x));若要完全解决以上的plot命令warning问题,可在配置文件
/usr/local/share/octave/site/m/startup/octaverc 中添加以下代码:
graphics_toolkit('gnuplot')Octave界面式启动及示例
输入以下命令进行Octave界面式启动:
octave启动后可进入以下可视化界面:
示例如下:
>> a = magic(2)
a =
4 3
1 2
>> a(1,:) = 0
a =
0 0
1 2绘图数据
绘图数据(Plotting Data)
当开发学习算法时,往往几个简单的图,可以让你更好地理解算法的内容,并且可以完整地检查下算法是否正常运行,是否达到了算法的目的。
例如在之前的视频中,我谈到了绘制成本函数,可以帮助确认梯度下降算法是否收敛。通常情况下,绘制数据或学习算法所有输出,也会启发你如何改进你的学习算法。幸运的是,Octave有非常简单的工具用来生成大量不同的图。当我用学习算法时,我发现绘制数据、绘制学习算法等,往往是我获得想法来改进算法的重要部分。在这段视频中,我想告诉你一些Octave的工具来绘制和可视化你的数据。
>> x=linspace(-10,10);
>> plot(x,sin(x));控制语句
控制语句 for,while,if语句
向量 的值就是这样一个集合 2的一次方、2的二次方,依此类推。这就是我的 等于 1 到 10的语句结构,让 遍历 1 到 10的值。
另外,你还可以通过设置你的 indices (索引) 等于 1一直到10,来做到这一点。这时indices 就是一个从1到10的序列。
你也可以写 i = indices,这实际上和我直接把 i 写到 1 到 10 是一样。你可以写 disp(i),也能得到一样的结果。所以 这就是一个 “for” 循环。
如果你对 “break” 和 “continue” 语句比较熟悉,Octave里也有 “break” 和 “continue”语句,你也可以在 Octave环境里使用那些循环语句。
向量化
向量化(Vectorization)
我将介绍有关向量化的内容,无论你是用Octave,还是别的语言,比如MATLAB或者你正在用Python、NumPy 或 Java C C++,所有这些语言都具有各种线性代数库,这些库文件都是内置的,容易阅读和获取,他们通常写得很好,已经经过高度优化,通常是数值计算方面的博士或者专业人士开发的。
而当你实现机器学习算法时,如果你能好好利用这些线性代数库,或者数值线性代数库,并联合调用它们,而不是自己去做那些函数库可以做的事情。如果是这样的话,那么通常你会发现:首先,这样更有效,也就是说运行速度更快,并且更好地利用你的计算机里可能有的一些并行硬件系统等等;其次,这也意味着你可以用更少的代码来实现你需要的功能。因此,实现的方式更简单,代码出现问题的有可能性也就越小。
举个具体的例子:与其自己写代码做矩阵乘法。如果你只在Octave中输入乘以就是一个非常有效的两个矩阵相乘的程序。有很多例子可以说明,如果你用合适的向量化方法来实现,你就会有一个简单得多,也有效得多的代码。
如果你想要计算 ,注意到右边是求和,那么你可以自己计算 到 的和。但换另一种方式来想想,把 看作,那么你就可以写成两个向量的内积,其中就是、、,如果你有两个特征量,如果 ,并且如果你把 看作、、,这两种思考角度,会给你两种不同的实现方式。
逻辑回归(Logistic Regression)
如果我们要用线性回归算法来解决一个分类问题,对于分类, 取值为 0 或者1,但如果你使用的是线性回归,那么假设函数的输出值可能远大于 1,或者远小于0,即使所有训练样本的标签 都等于 0 或 1。尽管我们知道标签应该取值0 或者1,但是如果算法得到的值远大于1或者远小于0的话,就会感觉很奇怪。所以我们在接下来的要研究的算法就叫做逻辑回归算法,这个算法的性质是:它的输出值永远在0到 1 之间。
顺便说一下,逻辑回归算法是分类算法,我们将它作为分类算法使用。有时候可能因为这个算法的名字中出现了“回归”使你感到困惑,但逻辑回归算法实际上是一种分类算法,它适用于标签 取值离散的情况,如:1 0 0 1。
根据线性回归模型我们只能预测连续的值,然而对于分类问题,我们需要输出0或1,我们可以预测:
参考文章 Octave教程(Octave Tutorial)