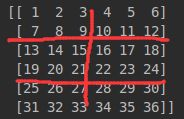
假设下图矩阵,按照红线切分成 6 个子矩阵,原矩阵成为分块矩阵
- patch size: 2x3
- rows=3, cols=2
用两个 for 循环肯定可以解决问题,但是今天采用两种新方法。
方法 1:np.lib.stride_tricks.as_strided
import numpy as np
a = np.arange(1, 37).reshape(6, 6)
a = np.lib.stride_tricks.as_strided(
a,
shape=(3, 2, 2, 3), # 要输出矩阵的 shape
strides=a.itemsize * np.array([12, 3, 6, 1])
)
print(a)
strides:
-
a.itemsize=8,因为a.dtype = int64,表示 8 个字节
后面的 array 告诉函数 怎么索引原矩阵数据组成新矩阵
从右往左依次是: - 1,子矩阵内 列与列 相隔的元素数量,如 1, 2
- 6,子矩阵内 行与行 相隔的元素数量,如 1, 7
- 3,子矩阵间 列与列 相隔的元素数量,如 1, 4
- 12,子矩阵间 行与行 相隔的元素数量,如 1, 13
同样的,可以将此方法拓展到 3D 矩阵,就能方便地将图片转化成 patches.
import numpy as np
# dummy image
a = np.array([[x, x, x] for x in range(1, 37)]).reshape((6, 6, 3))
a = np.lib.stride_tricks.as_strided(
a,
shape=(3, 2, 2, 3, 3),
strides=a.itemsize * np.array([12 * 3, 3 * 3, 6 * 3, 1 * 3, 1])
)
# cvt batchs = 3x2 = 6
a = a.reshape((-1, 2, 3, 3))
print(a)
注意:
- 转化子图,也要以 3×2 的形式,不能在 shape 那里直接指定 batch,可以再加一步 reshape 来指定。
- strides 这里是 5 维,要记得最里面的元素间隔还是 1,外边的要 ×3
图片实例
import numpy as np
import cv2
import os
a = cv2.imread('aerials/Afghan_2003258.jpg')
img_h, img_w, _ = a.shape # (1400, 1800, 3)
subimg_h, subimg_w = 700, 900
a = np.lib.stride_tricks.as_strided(
a,
shape=(img_h // subimg_h, img_w // subimg_w, subimg_h, subimg_w, 3), # rows, cols
strides=a.itemsize * np.array([subimg_h * img_w * 3, subimg_w * 3, img_w * 3, 1 * 3, 1])
)
# cvt batchs
a = a.reshape((-1, subimg_h, subimg_w, 3))
out_dir = 'aerials/split'
for idx, subimg in enumerate(a):
cv2.imwrite(os.path.join(out_dir, 'Afghan_2003258_%d.jpg' % idx), subimg)
缺点:如果原图 h,w 不能被子图 h,w 整除,会丢失右侧和下侧部分数据
如下图子图为 400x400,丢失了右侧 200 列 和 下侧 200 行数据。
方法 2:reshape + transpose
inspired by ShuffleNet
import numpy as np
a = np.arange(1, 37).reshape(6, 6)
a = a.reshape(3, 2, 2, 3)
a = np.transpose(a, [0, 2, 1, 3])
print(a)
After reshape,原始矩阵是横着索引的,并不是我们想要的
[[[[ 1 2 3]
[ 4 5 6]]
[[ 7 8 9]
[10 11 12]]]
[[[13 14 15]
[16 17 18]]
[[19 20 21]
[22 23 24]]]
[[[25 26 27]
[28 29 30]]
[[31 32 33]
[34 35 36]]]]
After transpose,转换第 2 维 和 第 3 维,就对了
[[[[ 1 2 3]
[ 7 8 9]]
[[ 4 5 6]
[10 11 12]]]
[[[13 14 15]
[19 20 21]]
[[16 17 18]
[22 23 24]]]
[[[25 26 27]
[31 32 33]]
[[28 29 30]
[34 35 36]]]]