【NLP篇-分词】分词的几种方法综述
第一部分:分词的方法概述
- 基于词表: 正向最大匹配法、逆向最大匹配法
- 基于统计: 基于N-gram语言模型的分词方法
- 基于序列标注: 基于HMM/CRF/DeepLearning的端到端的分词方法
第二部分:方法简要说明
- 正向最大匹配法:
- 逆行向最大匹配法:
这种基于词表的方法,前提是有一个已经分的较好的词表,然后匹配。正向与逆向只是匹配的方式不同而已。这种基于词表的方法,前提是有一个已经分的较好的词表,然后匹配。正向与逆向只是匹配的方式不同而已。详细见:百科 - N-gram语言模型分词
随机变量S是一个汉字的序列,W是S上所有可能的切分路径。求解使条件概率P(W|S)最大的切分路径W*。
W ∗ = a r g m a x P ( W ∣ S ) W* = argmaxP(W|S) W∗=argmaxP(W∣S)
根据贝叶斯公式:
W ∗ = a r g m a x P ( W ) P ( W ∣ S ) ) P ( S ) ) W* = argmax\frac{P(W)P(W|S))}{P(S))} W∗=argmaxP(S))P(W)P(W∣S))
其中,P(W|S)为恒定的值1.P(S)为归一化因子。所以求P(W)即可。 - 基于HMM的分词
分词问题就是对句子中的每个字打标注,标注要么是一个词的开始(B),要么是一个词的中间位置(M),要么是一个词的结束位置(E),还有单个字的词,用S表示。例如:
| 我 | 喜 | 欢 | 在 | 黑 | 龙 | 江 |
|---|---|---|---|---|---|---|
| S | B | E | S | B | M | E |
做简单的描述:
设观察集合为: O = { o 1 , o 2 , o 3 , . . . , o k } O = \left \{ { o_{1}, o_{2},o_{3}, ... ,o_{k} }\right \} O={o1,o2,o3,...,ok}
状态集合为: S = { s 1 , s 2 , s 3 , . . . , s k } S=\left \{ { s_{1}, s_{2},s_{3},..., s_{k} }\right \} S={s1,s2,s3,...,sk}
当输入观察序列为: X = x 1 , x 2 , x 3 , . . . , x n ; x i ∈ O X = { x_{1}, x_{2},x_{3}, ... ,x_{n};x_{i} ∈O } X=x1,x2,x3,...,xn;xi∈O
得到对应的状态序列: Y = y 1 , y 2 , y 3 , . . . , y n ; y i ∈ S Y= { y_{1}, y_{2}, y_{3}, ... ,y_{n};y_{i}∈S } Y=y1,y2,y3,...,yn;yi∈S
基于HMM的分词方法:属于由字构词的分词方法,由字构词的分词方法思想并不复杂,它是将分词问题转化为字的分类问题(序列标注问题)。从某些层面讲,由字构词的方法并不依赖于事先编制好的词表,但仍然需要分好词的训练语料。
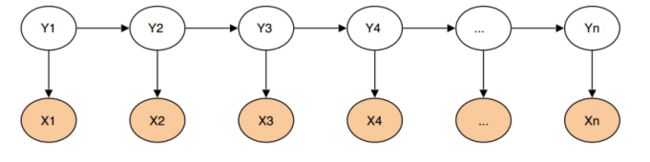
- 基于CRF的分词
HMM是生成式模型,而CRF是判别式模型,CRF通过定义条件概率p(Y|X)来描述模型。基于CRF的分词的模型的求解方法和传统ML算法类似,给定feature(字级别的各种信息)输出lable(词位)
s c o r e ( l ∣ s ) = ∑ j = 1 m ∑ i = 1 m λ i f j ( s , i , l i , l i − 1 ) score(l|s) = \sum_{j=1}^ {m} \sum_{i=1}^{m}{\lambda i}{f_{j}}(s,i,l_{i},l_{i-1}) score(l∣s)=∑j=1m∑i=1mλifj(s,i,li,li−1)
解释:
分词所使用的是Linear-CRF,它由一组特征函数组成,包括权重λ和特征函数f,特征函数f的输入是整个句子s、当前 p o s i pos_{i} posi 、前一个词位 l i − 1 l_{i-1} li−1,当前词位 l i l_{i} li。
CRF的 分词原理:
CRF把分词当做成字的词位的分类问题,通常定义字的词位信息如下:
词首,常用B表示;
词中,常用M表示;
词尾,常用E表示;
单子词,常用S表示。
备:和HMM做法类似。
比较:
| 类型 | CRF | vs | 基于词表 |
|---|---|---|---|
| 速度上 | 周期长,计算量大 | 高效 | |
| 歧义词/未登录词 | 较好。考虑词出现的频率+上下文语境信息 |
| 类型 | CRF | vs | HMM |
|---|---|---|---|
| 上下文 | 可以 | 其输出独立性假设,导致其不能考虑上下文的特征,限制了特征的选择 | |
| 局部的最优值 | 最大熵隐马模型则解决了隐马的无上下文的问题,可以任意选择特征,但由于其在每一节点都要进行归一化,只能找到局部最优解 | 其并不在每一个节点进行归一化,而是所有特征进行全局归一化,因此可以求得全局的最优值 |
- 基于深度学习的端到端的分词方法
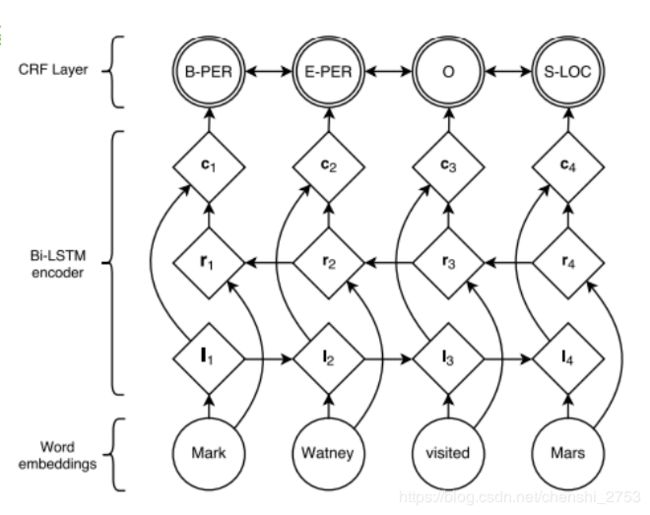
解释:
输入层为wordembedding,经过 双向LSTM网络编码,输出层是一个CRF层,经过LSTM网络输出的实际上是当前位置对于各词性的得分,CRF是对词性得分加上前一位置的词性概率转移的约束,其好处是引入一些语法规则的先验信息。
数学公式表示为:
S ( X , Y ) = ∑ i = 0 n A y i , y i − 1 + ∑ i − 1 n P i , y i S(X,Y) = \sum_{i=0}^{n}A_{y_{i},y_{i-1}} + \sum_{i-1}^{n}P_{i,y_{i}} S(X,Y)=∑i=0nAyi,yi−1+∑i−1nPi,yi
其中,A是词性的转移矩阵,P是BiLSTM网络的判别得分。
P ( y ∣ X ) = e s ( X , y ) ∑ y ⊂ y x A e s ( X , y ) P(y|X) = \frac{e^{s(X,y)}}{\sum_{y\subset y_{x}}^{A}e^{s(X,y)}} P(y∣X)=∑y⊂yxAes(X,y)es(X,y)