八叉树及K-D树的应用和实现
1. 八叉树、k-d树的原理
2. 八叉树、k-d树的应用、优缺点
3. 八叉树、k-d树的实现
八叉树和k-d树都经常用来处理三维空间数据,k-d树的使用范围更宽泛些,适用于k维空间的数据,在Sift算法中,k-d树被用于在k维的空间内搜索邻近特征点。
1. 八叉树、k-d树的原理
wiki或百科上面都有详细的介绍。
http://en.wikipedia.org/wiki/K-d_tree
http://en.wikipedia.org/wiki/Octree
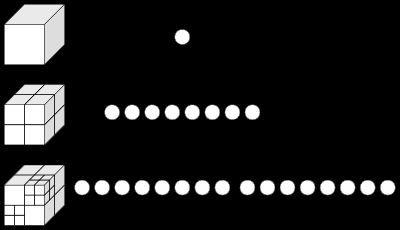
八叉树,一个立方体等分为八份,并可以持续的细分下去,虽然每个节点都能分出八个叉,但形象,且等分空间,简单容易理解。我曾经应用八叉树来离散化一个三角片表示的曲面,离散曲面。
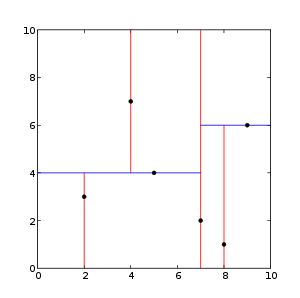
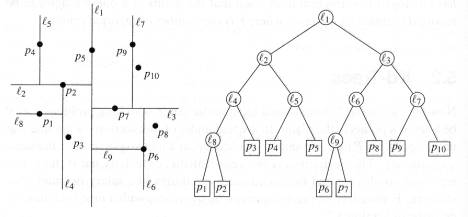
单看下面的k-d树的图示,就让人眼晕了,虽然k-d树只有两个叉。眼晕的主要原因就是空间不等分。所以,只要理解k-d树划分空间的依据,剩下的细节都与八叉树类似了。其实k-d树叶可以有均分的模式,只要让划分依据变为node的中心点就行了,只不过这样做k-d的效率就不高了。
从下图看,其k-d每个节点划分的依据是 挑选一个维度,在这个维度上 找到 本节点内所有点的中值点,然后,进行划分。
k-d树的其他划分依据:
取本节点内所有点的重心。
均分法。
使用这些方法时,要注意建树时的终止条件,避免陷入无限的循环(或递归)中。
(src: http://homes.ieu.edu.tr/hakcan/projects/kdtree/kdTree.html)
2. 八叉树、k-d树的应用、优缺点
八叉树一般都用于三维空间,若二维空间,可以用四叉树,原理是一模一样的。八叉树,常用于离散化空间,数据划分存储,数据查找等。
k-d树虽然是二叉树,却适用于k维的空间,而且在k邻域查找时,比较有优势。k-d也长用于数据划分存储,邻域查找等。
二者特性的比较:
八叉树算法的算法实现简单,但大数据量点云数据下,其使用比较困难的是最小粒度(叶节点)的确定,粒度较大时,有的节点数据量可能仍比较大,后续查询效率仍比较低,反之,粒度较小,八叉树的深度增加,需要的内存空间也比较大(每个非叶子节点需要八个指针),效率也降低。而等分的划分依据,使得在数据重心有偏斜的情况下,受划分深度限制,其效率不是太高。
k-d在邻域查找上比较有优势,但在大数据量的情况下,若划分粒度较小时,建树的开销也较大,但比八叉树灵活些。在小数据量的情况下,其搜索效率比较高,但在数据量增大的情况下,其效率会有一定的下降,一般是线性上升的规律。
也有将八叉树和k-d树结合起来的应用,应用八叉树进行大粒度的划分和查找,而后使用k-d树进行细分,效率会有一定的提升,但其搜索效率变化也与数据量的变化有一个线性关系。
3. 八叉树、k-d树的实现
采用递归的方式,代码比较简单,逻辑明了,前提是对递归不要太陌生。
网上有很多Octree的实现和库。如
http://www.flipcode.com/archives/Octree_Implementation.shtml
http://code.google.com/p/efficient-sparse-voxel-octrees/
http://akbar.marlboro.edu/~mahoney/support/alg/alg/node41.html
http://nomis80.org/code/octree.html
opencv中的也有octree的实现
Octree建树的逻辑:
自定义哪些数据类型?
tree类型,node类型;
每个节点应该包含哪些数据?
8个子节点指针,本节点的中心(划分与搜索的依据)和半径,点的个数,和子节点保存数据的容器
常用的手法是非叶子节点的点的个数为0,容器内无数据
如何划分数据?如何建立索引?
每个节点都会保存自己的中心坐标和半径,子节点保存数据,非子节点一般不保存数据,有了中心半径和本节点内的数据,就能划分建树,或者搜索
BuildTree(数据集, 数据个数, 中心,半径,当前深度) // 递归建树函数
确定递归停止条件和动作,count < num_threshold 或 递归深度达到最大 时,为子节点
并保存子节点数据和个数
若无中心和半径,计算数据集的最小包围盒半径和中心
依据中心和半径,将数据划分为八份,计算八个子节点的中心和半径
进行新的八次递归建树 child[i]->BuildTree(新的数据集,新的数据个数,新的中心、半径,深度+1).
删除临时数据容器,释放内存
Search(point)
确定递归停止条件:子节点的个数为小于阈值,或递归深度达到最大
搜遍本节点内的数据,查找给定的点,若找到,返回true,找不到,返回false
取本节点的中心和半径,计算出应该在下一层那个子节点进行搜索,如k
子节点递归搜索,child[k]->search(point);
K-D树的逻辑:
自定义数据类型?
tree: 提供建树和搜索的接口
node节点,node节点里包含中心,半径,划分的维度,两个子节点指针,数据容器(子节点专用)
如何划分数据?
每个node计算数据的包围盒,每个维度的宽度,最大宽度的维度用于划分,计算中心(重心法,或排序中值法),然后子节点继续划分
Build()
确定递归停止条件,本节点数据点数小于阈值,或达到最大深度,为子节点,保存数据。
由本节点的数据,计算包围盒,每个维度的宽度,最大宽度的维度用于划分计算中心(重心法,或排序中值法),然后划分数据
子节点由划分的数据继续下一步的划分建树child[i]->build()
最邻近点搜索,递归法:
find_closest_point(point)
确认本节点是子节点,停止递归,计算本节点内最邻近的点,及距离d。
若非子节点:
计算点到分割面的距离spd, 为正数,child[0]->find_closest_point(point),在子节点0中继续搜索。
若计算出的最近点距离d 大于 分割面距离 spd,则仍需要在节点1中继续搜索最邻近点。
若距离分割面是非正数,在子节点1中搜索。
若计算出的最近点距离d 大于 分割面距离 spd,则仍需要在节点0中继续搜索最邻近点。