深度学习——神经网络最优化方法

最优化方法

本文只对吴恩达最优化方法中原理部分进行整理，没有代码部分，需要原始代码可以到GitHub上down下来。文尾附链接。

除了使用Gradient Descent更新参数降低成本，还有更多高级优化方法，这些方法可以加快学习速度，甚至可以获得更好的COST函数最终值。 拥有一个好的优化算法可能是等待天数与短短几个小时之间的差异，以获得同样的效果。最优化方法做的就是加速训练。

梯度下降在成本函数上“下坡” $J$. 把它想象成它试图这样做:

图1 : 最小化cost就像找到丘陵中的最低点
在训练的每个步骤中，您都会按照特定方向更新参数，以尝试达到最低点。

注意: 本文中, 目标函数J对特参数a的导数用da表示：$\frac{\partial J}{\partial a } = $ da 。

1 - 梯度下降 Gradient Descent

机器学习中的一种简单优化方法是梯度下降（Gradient Descent , GD）。 当您对每个步骤的所有$ m $示例执行梯度下降操作时，它也称为Batch Gradient Descent。

Gradient Descent：实施梯度下降更新规则。 梯度下降规则是，对于$l=1，...，L$：
$$W^{[l]}=W^{[l]}-\alpha d{W}^{[l]}\text{\hspace{1em}(1)}$$
$$b^{[l]}=b^{[l]}-\alpha d{b}^{[l]}\text{\hspace{1em}(2)}$$
其中L是层数，$alpha$是学习率。

其中一个变体是随机梯度下降（SGD），相当于小批量梯度下降，其中每个小批量只有一个例子。 您刚刚实施的更新规则不会更改。 您将在一次只计算一个训练示例而不是整个训练集上计算渐变的变化是什么。 下面的代码示例说明了随机梯度下降和（批量）梯度下降之间的差异。

• 批量梯度下降(Batch) Gradient Descent:

X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
    # Forward propagation
    a, caches = forward_propagation(X, parameters)
    # Compute cost.
    cost = compute_cost(a, Y)
    # Backward propagation.
    grads = backward_propagation(a, caches, parameters)
    # Update parameters.
    parameters = update_parameters(parameters, grads)
        

• 随机梯度下降Stochastic Gradient Descent:

X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
    for j in range(0, m):
        # Forward propagation
        a, caches = forward_propagation(X[:,j], parameters)
        # Compute cost
        cost = compute_cost(a, Y[:,j])
        # Backward propagation
        grads = backward_propagation(a, caches, parameters)
        # Update parameters.
        parameters = update_parameters(parameters, grads)

2 - Mini-Batch Gradient descent

下面对Mini-Batch Gradient descent进行介绍，测试集为(X, Y)。

总共有两步:

• 重新随机排序shuffle: 将训练集（X，Y）的重新排序，如下所示。 X和Y的每一列代表一个训练样例。 注意重新随机排序是在X和Y之间同步完成的。这样在洗牌之后，X的$i^{th}$列是对应于Y中的$i^{th}$标签的示例。重新排序使这些例子被随机分配到不同的mini-batches中去。
  
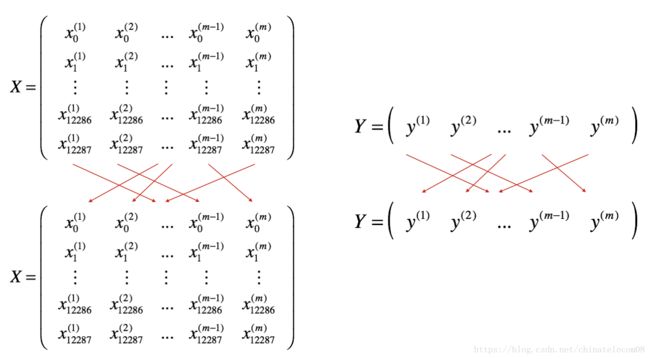
• Partition分区: 将重新排序后的训练集（X，Y）分区为大小为mini_batch_size（此处为64）的mini-batches。 请注意，训练示例的数量并不总是被mini_batch_size整除。 最后一个迷你批次可能更小，但您不必担心这一点。 当最终的小批量小于完整的mini_batch_size时，它将如下所示：
  

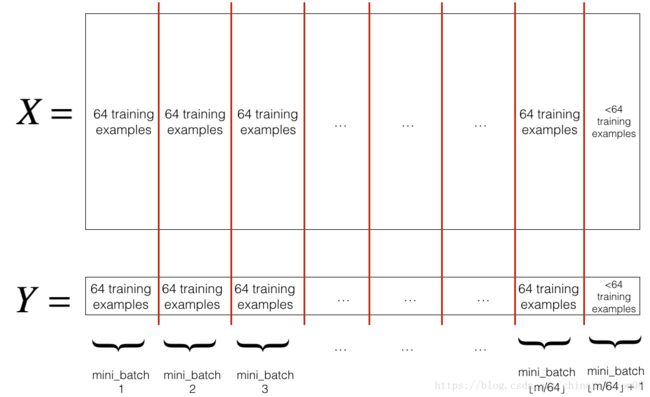
请注意，最后一个小批量可能最终小于mini_batch_size = 64。让$\lfloor s\rfloor$ 代表$s$向下舍入到最接近的整数（这是Python中的math.floor(s)。 如果示例的总数不是mini_batch_size=64的倍数，那么将会有$\lfloor \frac{m}{mini\_batch\_size}\rfloor$ 最终小批量中的示例将是($m-min{i}_{\_}batc{h}_{\_}size\times \lfloor \frac{m}{mini\_batch\_size}\rfloor$)。

注意:

• Shuffling和Partitioning是构建迷你批次所需的两个步骤
• 通常选择2的幂为mini_batch，例如16,32,64,128。

3 - 动量Momentum

因为mini-batch梯度下降在仅仅看到一个例子的子集之后进行参数更新，所以更新的方向具有一些变化，因此小批量梯度下降所采用的路径将沿着局部最优收敛方向摆动。 使用Momentum可以减少这些振荡。
Momentum考虑了过去的梯度方向以平滑更新。我们将先前收敛的方向存储在变量$v$中。 形式上，这将是先前步骤的梯度的指数加权平均值。 您还可以将$v$视为滚球下坡的“速度”，根据坡度/坡度的方向建立速度（和动量）。

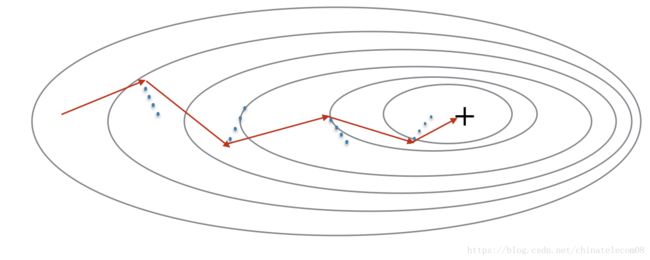
Figure 3: 红色箭头显示了使用动量梯度下降的mini-batch的下降方向。 蓝点表示未使用动量优化的梯度方向（相对于当前的mini-batch）。 我们让梯度影响速度方向$v$，然后每一步调整$v$的方向，而不是仅仅使$v$等于梯度方向。

动量momentum公式:
使用momentum优化梯度下降的公式如下。对于网络的每一层 $l=1,...,L$：

$$\{\begin{array}{l}{v}_{d{W}^{[l]}}=\beta v_{d{W}^{[l]}}+(1-\beta )d{W}^{[l]}\\ W^{[l]}=W^{[l]}-\alpha v_{d{W}^{[l]}}\end{array}\text{\hspace{1em}(3)}$$

$$\{\begin{array}{l}{v}_{d{b}^{[l]}}=\beta v_{d{b}^{[l]}}+(1-\beta )d{b}^{[l]}\\ b^{[l]}=b^{[l]}-\alpha v_{d{b}^{[l]}}\end{array}\text{\hspace{1em}(4)}$$

L代表神经网络的某一层，$\beta$ 是动量momentum ，$\alpha$是学习率。

注意：

• 用零初始化速度 $v$。 因此，该算法将需要几次迭代来“建立”速度并开始开始有较快的速度。
• 如果 $\beta =0$，那么这只是没有动量的标准梯度下降。

你如何选择 $\beta$？

• 动量 $\beta$ 越大，更新越平滑，因为我们将过去的渐变考虑得越多。 但是，如果$beta$太大，它也可能会使更新过于平滑。
• $\beta$的常用值范围为0.8到0.999。 如果你不想调整它，$\beta =0.9$通常是合理的默认值。
• 调整模型的最佳 $\beta$ 可能需要尝试多个值才能看到在减少成本函数$J$的值方面最有效的方法。

注意：

• 动量将过去的梯度考虑在内，以平滑梯度下降的步骤。 它可以应用于批量梯度下降，小批量梯度下降或随机梯度下降。
• 你必须调整动量超参数$\beta$和学习率$\alpha$。
  

4 - Adam

Adam是用于训练神经网络的最有效的优化算法之一。 它结合了RMSProp和Momentum的想法。

Adam 是如何工作的？

1. 它计算过去梯度的指数加权平均值，并将其存储在变量$v$（偏差校正前）和$v^{correct}$（偏差校正）中。
2. 它计算过去梯度的平方的指数加权平均值，并将其存储在变量$s$（偏差校正前）和$s^{correct}$（偏差校正）中。
3. 它基于来自“1”和“2”的组合信息更新参数改变方向。

参数跟新准则如下，对于网络每一层参数 $l=1,...,L$:

$$\{\begin{array}{l}{v}_{d{W}^{[l]}}={\beta }_1{v}_{d{W}^{[l]}}+(1-{\beta }_1)\frac{\partial \mathcal{J}}{\partial W^{[l]}}\\ v_{d{W}^{[l]}}^{corrected}=\frac{v_{d{W}^{[l]}}}{1-({\beta }_1{)}^t}\\ s_{d{W}^{[l]}}={\beta }_2{s}_{d{W}^{[l]}}+(1-{\beta }_2)(\frac{\partial \mathcal{J}}{\partial W^{[l]}}{)}^2\\ s_{d{W}^{[l]}}^{corrected}=\frac{s_{d{W}^{[l]}}}{1-({\beta }_1{)}^t}\\ W^{[l]}=W^{[l]}-\alpha \frac{v_{d{W}^{[l]}}^{corrected}}{\sqrt{s_{d{W}^{[l]}}^{corrected}}+\epsilon }\end{array}$$
这里：

• t为每层参数执行Adam的次数
• L是层数
• ${\beta }_1$和${\beta }_2$是超参数，可控制两个指数值加权平均值。
• $\alpha$是学习率
• $\epsilon$是一个非常小的数字，以避免除以零

5 - 总结

Adam明显优于小批量梯度下降和动量。 如果您在此简单数据集上运行模型以获得更多时期，则所有这三种方法都将产生非常好的结果。 但是，你已经看到Adam收敛得更快。

Adam的一些优点包括：

• 相对较低的内存要求（虽然高于梯度下降和带动量的梯度下降）
• 即使很少调整超参数（除了$\alpha$），通常效果很好

---

资料地址GitHub，顺手点赞
资料原地址GitHub

转载请注明出处audior