使用Python的Swampy程序包中的“乌龟”画花朵,螺旋线,打字等
练习4-2
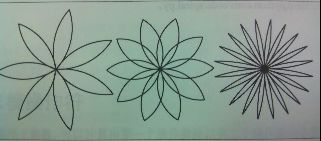
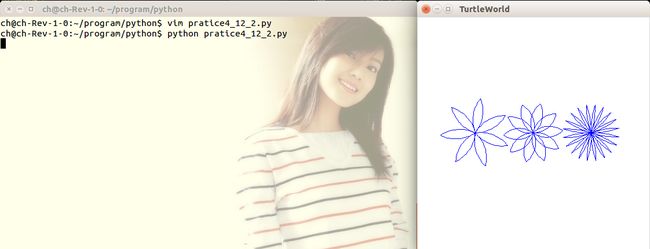
写一组合适的通用函数,用来画出下图所示的花朵图案。
这个是搬运过来的,代码如下:
from swampy.TurtleWorld import *
from math import *
def polyline(t,n,length,angle):
for i in range(n):
fd(t,length)
lt(t,angle)
def arc(t,r,angle):
arc_length = 2 * pi * r * abs(angle) /360
n = int(arc_length/4) + 1
step_length = arc_length / n
step_angle = float(angle) / n
lt(t,step_angle/2)
polyline(t,n,step_length,step_angle)
rt(t,step_angle/2)
def petal(t,r,angle):
for i in range(2):
arc(t,r,angle)
lt(t,180-angle)
def flower(t,n,r,angle):
for i in range(n):
petal(t,r,angle)
lt(t,360.0/n)
def move(t,length):
pu(t)
fd(t,length)
pd(t)
world = TurtleWorld()
bob = Turtle()
bob.delay = 0.01
move(bob,-100)
flower(bob,7,60.0,60.0)
move(bob,100)
flower(bob,10,40.0,80.0)
move(bob,100)
flower(bob,20,140.0,20.0)
die(bob)
world.canvas.dump()
wait_for_user()
由于对画图不是很感兴趣,感觉实习以后用不着,没花心思做,下面的代码还是搬运来的。
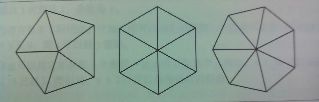
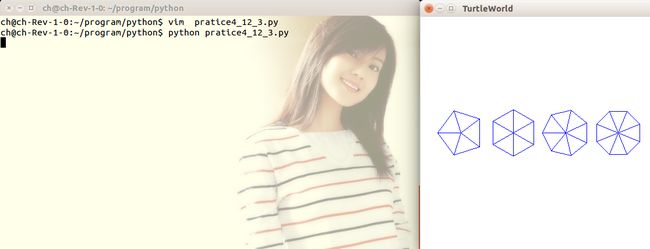
4-3 写一组合适的通用函数,用来画出下图所示的图形。
代码如下:
from math import *
from swampy.TurtleWorld import *
def draw_pie(t,n,r):
polypie(t,n,r)
pu(t)
fd(t,r*2+10)
pd(t)
def polypie(t,n,r):
angle = 360.0/n
for i in range(n):
isosceles(t,r,angle/2)
lt(t,angle)
def isosceles(t,r,angle):
y = r*sin(angle*pi/180)
rt(t,angle)
fd(t,r)
lt(t,90+angle)
fd(t,2*y)
lt(t,90+angle)
fd(t,r)
lt(t,180-angle)
world = TurtleWorld()
bob = Turtle()
bob.delay = 0
pu(bob)
bk(bob,130)
pd(bob)
size = 40
draw_pie(bob,5,size)
draw_pie(bob,6,size)
draw_pie(bob,7,size)
draw_pie(bob,8,size)
die(bob)
world.canvas.dump()
wait_for_user()
4-4 字母表中的字母可以使用一些基本元素来构成。如横线,竖线以及一些曲线。设计一个字体,可以使用最少的基本元素画出来,并编写函数来画出字母表中的所有的字母。
你应当给每个字母单独写一个函数,名为 draw_a,draw_b 等,并把这些函数放到letters.py文件中。可以从http://thinkpython.com/code/typewriter.py下载一个“乌龟打字机”来帮助测试你的代码。
letters.py代码如下 :
from swampy.TurtleWorld import *
from polygon import *
#level 0 primitives are provided by World.py
#They include fd,bk,lt,rt,pu and pd
#level 1 primitives are simple combinations of level 0 primitives
#They have no pre-or post-conditions
def fdlt(t,n,angle = 90):
"""forward and left"""
fd(t,n)
lt(t,angle)
def fdbk(t,n):
"""forward and back,ending at the original position"""
fd(t,n)
bk(t,n)
def skip(t,n):
"""lift the open and move"""
pu(t)
fd(t,n)
pd(t)
def stump(t,n,angle=90):
"""make a vertical line and leave the turtle at the top
facing right
"""
lt(t)
fd(t,n)
rt(t,angle)
def hollow(t,n):
"""move the turtle vertically and leave it at the top,
facing right"""
lt(t)
skip(t,n)
rt(t)
#level 2 primitives use primitives from level0 and 1
#to draw posts(vertical elements) and beams(horizontal elements)
#level 2 primitives always return the turtle to the original
#location and direction
def post(t,n):
"""make a vertical line and return to the original position"""
lt(t)
fdbk(t,n)
rt(t)
def beam(t,n,height):
"""make a horizontal line at the given height and return """
hollow (t,n*height)
fdbk(t,n)
hollow(t,-n*height)
def hangman(t,n,height):
"""make a vertical line to the given height and a horizontal line
at the given height and then return .
This is efficient to implement,and turns out to be useful,but
it is not so semantically clean."""
stump(t,n*height)
fdbk(t,n)
lt(t)
bk(t,n*height)
rt(t)
def diagonal(t,x,y):
"""make a diagonal line to the given x,y offsets and return"""
from math import atan2,sqrt,pi
angle = atan2(y,x)*180/pi
dist = sqrt(x**2+y**2)
lt(t,angle)
fdbk(t,dist)
rt(t,angle)
def vshape(t,n,height):
diagonal(t,-n/2,height*n)
diagonal(t,n/2,height*n)
def bump(t,n,height):
"""make a bump with radius n at height*n """
stump(t,n*height)
arc(t,n/2.0,180)
lt(t)
fdlt(t,n*height+n)
"""
The letter-drawing functions all have the precondtion
that the turtle is in the lower-left corner of the letter,
and postcondition that the turtle is in the lower-right
corner,facing in the direction it started in.
They all take a turtle as the first argument and a size(n)
as the second.Most letters are(n) units wide and(2n) units high
"""
def draw_a(t,n):
diagonal(t,n/2,2*n)
beam(t,n,1)
skip(t,n)
diagonal(t,-n/2,2*n)
def draw_b(t,n):
bump(t,n,1)
bump(t,n,0)
skip(t,n/2)
def draw_c(t,n):
hangman(t,n/2)
fd(t,n)
def draw_d(t,n):
bump(t,2*n,0)
skip(t,n)
def draw_ef(t,n):
hangman(t,n,2)
hangman(t,n,1)
def draw_e(t,n):
draw_ef(t,n)
fd(t,n)
def draw_f(t,n):
draw_ef(t,n)
skip(t,n)
def draw_g(t,n):
hangman(t,n,2)
fd(t,n/2)
beam(t,n/2,2)
fd(t,n/2)
post(t,n)
def draw_h(t,n):
post(t,2*n)
hangman(t,n,1)
skip(t,n)
post(t,2*n)
def draw_i(t,n):
beam(t,n/2)
fd(t,n/2)
post(t,2*n)
fd(t,n/2)
def draw_j(t,n):
beam(t,n,2)
arc(t,n/2,90)
fd(t,3*n/2)
skip(t,-2*n)
rt(t)
skip(t,n/2)
def draw_k(t,n):
post(t,2*n)
stump(t,n,180)
vshape(t,2*n,0.5)
fdlt(t,n)
skip(t,n)
def draw_l(t,n):
post(t,2*n)
fd(t,n)
def draw_n(t,n):
post(t,2*n)
skip(t,n)
diagonal(t,-n,2*n)
post(t,2*n)
def draw_m(t,n):
post(t,2*n)
draw_v(t,n)
post(t,2*n)
def draw_o(t,n):
skip(t,n)
circle(t,n)
skip(t,n)
def draw_p(t,n):
bump(t,n,1)
skip(t,n/2)
def draw_q(t,n):
draw_o(t,n)
diagonal(t,-n/2,n)
def draw_r(t,n):
draw_p(t,n)
diagonal(t,-n/2,n)
def draw_s(t,n):
fd(t,n/2)
arc(t,n/2,180)
arc(t,n/2,-180)
fdlt(t,n/2,-90)
skip(t,2*n)
lt(t)
def draw_t(t,n):
beam(t,n,2)
skip(t,n/2)
post(t,2*n)
skip(t,n/2)
def draw_u(t,n):
post(t,2*n)
fd(t,n)
post(t,2*n)
def draw_v(t,n):
skip(t,n/2)
vshape(t,n,2)
skip(t,n/2)
def draw_w(t,n):
draw_v(t,n)
draw_v(t,n)
def draw_x(t,n):
diagonal(t,n,2*n)
skip(t,n)
diagonal(t,-n,2*n)
def draw_y(t,n):
skip(t,n/2)
stump(t,n)
vshape(t,n,1)
rt(t)
fdlt(t,n)
skip(t,n/2)
def draw_z(t,n):
beam(t,n,2)
diagonal(t,n,2*n)
fd(t,n)
def draw_(t,n):
#draw a space
skip(t,n)
if _name_ == '_main_':
world = TurtleWorld()
#create and position the turtle
size = 20
bob = Turtle()
bob.delay = 0.01
for f in [draw_h,draw_e,draw_l,draw_o]:
f(bob,size)
skip(bob,size)
wait_for_user()