sklearn学习笔记:LDA和PCA降维
1. 导入需要的包:
# encoding: utf-8
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysisiris = datasets.load_iris()
iris_X = iris.data
iris_y = iris.target
print iris_X.shape
print iris.feature_names
print iris.target_names输出结果:
(150, 4)
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
['setosa' 'versicolor' 'virginica']3. 使用PCA将4维数据降至3维,并查看降维后的前5个样本数据:
print iris_X.shape
print iris_X[0:5]
model_pca = PCA(n_components = 4)
X_pca = model_pca.fit_transform(iris_X)
print X_pca.shape
print X_pca[0:5]
model_pca = PCA(n_components = 3)
X_pca = model_pca.fit_transform(iris_X)
print X_pca.shape
print X_pca[0:5]输出结果:
(150, 4)
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
(150, 4)
[[-2.68420713e+00 3.26607315e-01 -2.15118370e-02 1.00615724e-03]
[-2.71539062e+00 -1.69556848e-01 -2.03521425e-01 9.96024240e-02]
[-2.88981954e+00 -1.37345610e-01 2.47092410e-02 1.93045428e-02]
[-2.74643720e+00 -3.11124316e-01 3.76719753e-02 -7.59552741e-02]
[-2.72859298e+00 3.33924564e-01 9.62296998e-02 -6.31287327e-02]]
(150, 3)
[[-2.68420713 0.32660731 -0.02151184]
[-2.71539062 -0.16955685 -0.20352143]
[-2.88981954 -0.13734561 0.02470924]
[-2.7464372 -0.31112432 0.03767198]
[-2.72859298 0.33392456 0.0962297 ]]4. 将降至3维的数据进行绘制:
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
ax.scatter(X_pca[:, 0], X_pca[:, 1], X_pca[:, 2], marker='o', c=iris_y)
plt.show()输出结果:
5. 利用PCA将数据进一步降至2维:
model_pca = PCA(n_components=2)
X_pca = model_pca.fit_transform(iris_X)
print u"降维后各主成分方向", model_pca.components_
print u"降维后各主成分的方差值:", model_pca.expained_variance_
print u"降维后各主成分的方差值与总方差之比:", model_pca.explained_variance_ratio_降维后各主成分方向 [[ 0.36158968 -0.08226889 0.85657211 0.35884393]
[ 0.65653988 0.72971237 -0.1757674 -0.07470647]]
降维后各主成分的方差值: [4.22484077 0.24224357]
降维后各主成分的方差值与总方差之比: [0.92461621 0.05301557]6. 利用LDA将原始数据降至2维,因为LDA需要<=分类数-1,因此无法降至3维:
model_lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = model_lda.fit_transform(iris_X, iris_y)
print u"降维后各主成分的方差值与总方差之比:", model_lda.explained_variance_ratio_输出结果:
降维后各主成分的方差值与总方差之比: [0.99147248 0.00852752]
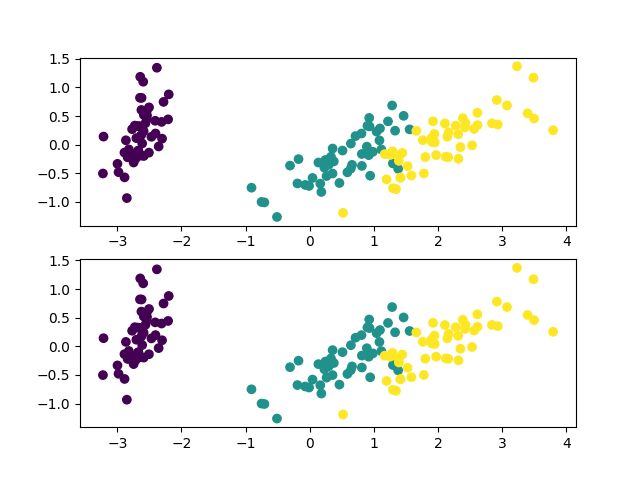
7. 将降至2维的数据进行绘图:
fig = plt.figure()
plt.subplot(211)
plt.scatter(X_pca[:, 0], X_pca[:, 1], marker='o', c=iris_y)
plt.subplot(212)
plt.scatter(X_pca[:, 0], X_pca[:, 1], marker='o', c=iris_y)
plt.show()输出结果:
8. 完整代码:
# encoding: utf-8
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
iris = datasets.load_iris()
iris_X = iris.data
iris_y = iris.target
print iris_X.shape
print iris.feature_names
print iris.target_names
print iris_X.shape
print iris_X[0:5]
model_pca = PCA(n_components = 4)
X_pca = model_pca.fit_transform(iris_X)
print X_pca.shape
print X_pca[0:5]
model_pca = PCA(n_components = 3)
X_pca = model_pca.fit_transform(iris_X)
print X_pca.shape
print X_pca[0:5]
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
ax.scatter(X_pca[:, 0], X_pca[:, 1], X_pca[:, 2], marker='o', c=iris_y)
plt.show()
model_pca = PCA(n_components=2)
X_pca = model_pca.fit_transform(iris_X)
print u"降维后各主成分方向", model_pca.components_
print u"降维后各主成分的方差值:", model_pca.explained_variance_
print u"降维后各主成分的方差值与总方差之比:", model_pca.explained_variance_ratio_
model_lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = model_lda.fit_transform(iris_X, iris_y)
print u"降维后各主成分的方差值与总方差之比:", model_lda.explained_variance_ratio_
fig = plt.figure()
plt.subplot(211)
plt.scatter(X_pca[:, 0], X_pca[:, 1], marker='o', c=iris_y)
plt.subplot(212)
plt.scatter(X_pca[:, 0], X_pca[:, 1], marker='o', c=iris_y)
plt.show()