支持向量机——SVM算法及例子（代码）
终于拖到最后一天交机器学习作业，选择了SVM算法，之前一直听说过，现在终于有了初步的了解，顺便post到这里分享一下，不足地方请大家指出
本文内容有来自《统计学习算法》（李航 著）第7章——支持向量机
同时也看了Stanford机器学习公开课
概要
支持向量机属于监督学习，是一种二类分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，支持向量机包括核心技巧，这使它成为实质上的非线性分类器。支持向量机的学习策略是间隔最大化，可形式化为一个求解凸二次规划的问题。
支持向量机学习方法包含构建由简至繁的模型：线性可分支持向量机、线性支持向量机及非线性支持向量机。简单模型是复杂模型的基础，也是复杂模型的特殊情况。当训练数据线性可分时，通过硬间隔最大化，学习一个线性的分类器，即线性可分支持向量机，又称为硬间隔支持向量机；当训练数据线性近似可分时，通过软间隔最大化，可学习一个线性的分类器，即线性支持向量机，又称为软间隔支持向量机；当训练数据线性不可分时，通过使用核及软间隔最大化，学习非线性支持向量机。
预备知识
函数间隔和几何间隔
KKT条件
线性可分支持向量机与硬间隔最大化
线性可分支持向量机
间隔最大化
支持向量和间隔边界
学习的对偶算法
线性支持向量机与软间隔最大化
非线性支持向量机与核函数
非线性支持向量机
核函数定义
Mercer定理
常用的核函数
实验
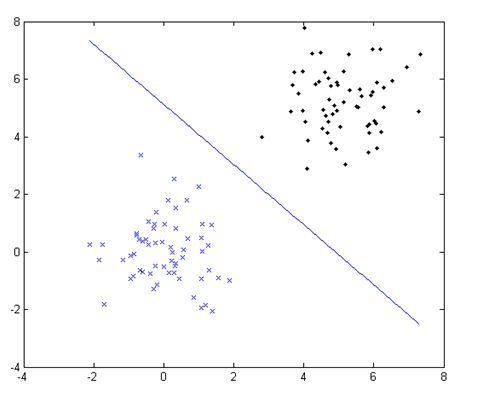
下面使用matlab构造一个线性可分训练数据集，利用线性支持向量机学习算法，通过求解目标函数的对偶问题得到最优解并计算分离超平面。
代码如下：
clear all
%构造两类训练数据集
n = 60;
randn('state',6);
x1 = randn(n,2); %2行N列矩阵
y1 = ones(n,1); %1*N个1
x2 = 5+randn(n,2); %2*N矩阵
y2 = -ones(n,1); %1*N个-1
figure;
plot(x1(:,1),x1(:,2),'bx',x2(:,1),x2(:,2),'k.');
hold on;
X = [x1;x2]; % 训练样本
Y = [y1;y2]; % 训练目标,n×1的矩阵,n为样本个数,值为+1或-1
tic
%解二次优化方程
n = length(Y);
H = (Y*Y').*(X*X'); % liner kernel
f = -ones(n,1);
A = [];
b = [];
Aeq = Y';
beq = 0;
lb = zeros(n,1);
ub = 100*ones(n,1);
a0 = zeros(n,1);
options = optimset;
options.LargeScale = 'off';
options.Display = 'off';
[a,fval,eXitflag,output,lambda]= quadprog(H,f,A,b,Aeq,beq,lb,ub,a0,options);
eXitflag
time=toc
%以下是分类平面：
Y2=a.*Y;
W(1)=sum(Y2.*(X(:,1)));
W(2)=sum(Y2.*(X(:,2)));
aLarge=find(a>0.1);
j=aLarge(1);
S(:,1)=Y.*a.*X(:,1);
S(:,2)=Y.*a.*X(:,2);
S2=S*(X(j,:)');
b=Y(j)-sum(S2);
xx1=min(X):0.1:max(X);
xx2=-(W(1)*xx1+b)/W(2);
plot(xx1,xx2);实验结果如下图所示：
